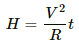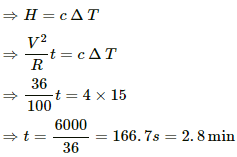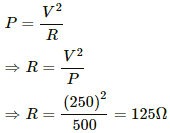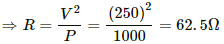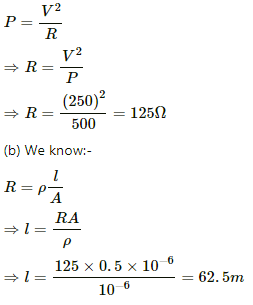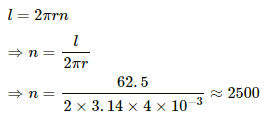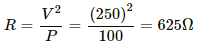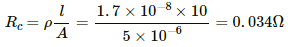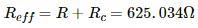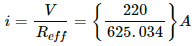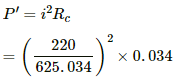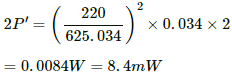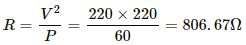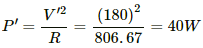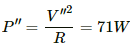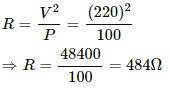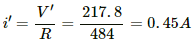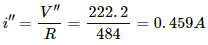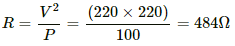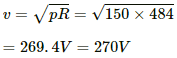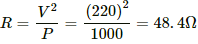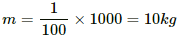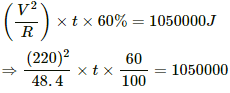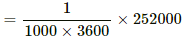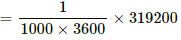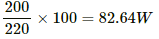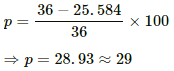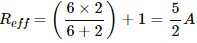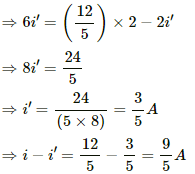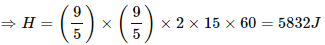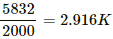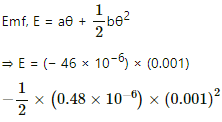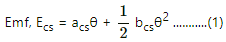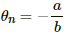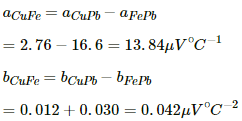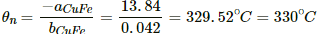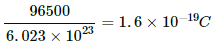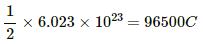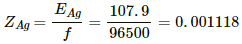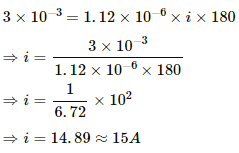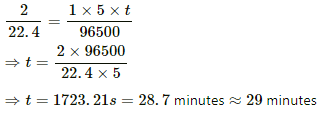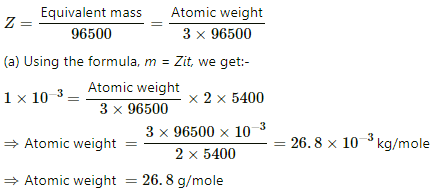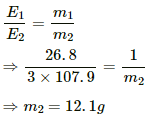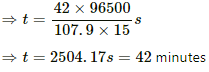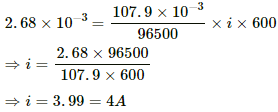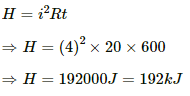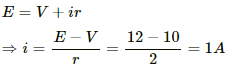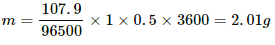HC Verma Questions and Solutions: Chapter 33: Thermal and Chemical Effects of Current- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. An electric current of 2.0 A passes through a wire of resistance 25 Ω. How much heat will be developed in 1 minute?
Given:-
Current through the wire, i = 2 A
Resistance of the wire, R = 25 Ω
Time taken, t = 1 min = 60 s
Heat developed across the wire,
H = i2Rt
= 2 × 2 × 25 × 60
= 100 × 60 J = 6000 J
Q.2. A coil of resistance 100 Ω is connected across a battery of emf 6.0 V. Assume that the heat developed in the coil is used to raise its temperature. If the heat capacity of the coil is 4.0 J K−1, how long will it take to raise the temperature of the coil by 15°C?
Given:-
Resistance of the coil, R = 100 Ω,
Emf of the battery, V = 6 V,
Change in temperature, ∆T = 15°C
Heat produced across the coil,
This heat produced is used to increase the temperature of the coil.
Q.3. The specification on a heater coil is 250 V, 500 W. Calculate the resistance of the coil. What will be the resistance of a coil of 1000 W to operate at the same voltage?
Let R be the resistance of the coil.
The power P consumed by a coil of resistance R when connected across a supply V is given by
Now, P = 1000 W
Q.4. A heater coil is to be constructed with a nichrome wire (ρ = 1.0 × 10−6 Ωm) that can operate at 500 W when connected to a 250 V supply. (a) What would be the resistance of the coil? (b) If the cross-sectional area of the wire is 0.5 mm2, what length of the wire will be needed? (c) If the radius of each turn is 4.0 mm, how many turns will be there in the coil?
(a) Let R be the resistance of the coil.
The power P consumed by a coil of resistance R when connected across a supply V is given by
(c) Let n be the number of turns in the coil. Then,
Q.5. A bulb with rating 250 V, 100 W is connected to a power supply of 220 V situated 10 m away using a copper wire of area of cross-section 5 mm2. How much power will be consumed by the connecting wires? Resistivity of copper = 1.7 × 10−8 Ωm.
Let R be the resistance of the bulb. If P is the power consumed by the bulb when operated at voltage V, then
Resistance of the copper wire,
The effective resistance,
The current supplied by the power station,
The power supplied to one side of the connecting wire,
The total power supplied on both sides,
Q.6. An electric bulb, when connected across a power supply of 220 V, consumes a power of 60 W. If the supply drops to 180 V, what will be the power consumed? If the supply is suddenly increased to 240 V, what will be the power consumed?
The resistance of a bulb that consumes power P and is operated at voltage V is given by
(a) Now the supply drops to V' = 180 V.
So, the power consumed,
(b) Now the supply increases to V" = 240 V. Therefore,
Q.7. A servo voltage stabiliser restricts the voltage output to 220 V ± 1%. If an electric bulb rated at 220 V, 100 W is connected to it, what will be the minimum and maximum power consumed by it?
Output voltage, V = 220 V ± 1% = 220 V ± 2.2 V
The resistance of a bulb that is operated at voltage V and consumes power P is given by
(a) For minimum power to be consumed, output voltage should be minimum. The minimum output voltage,
V' = (220 − 2.2) V
= 217.8 V
The current through the bulb,
Power consumed by the bulb, P' = i' × V'
= 0.45 × 217.8 = 98.0 W
(b) For maximum power to be consumed, output voltage should be maximum. The maximum output voltage,
V" = (220 + 2.2) V
= 222.2 V
The current through the bulb,
Power consumed by the bulb,
P" = i" × V"
= 0.459 × 222.2 = 102 W
Q.8. An electric bulb marked 220 V, 100 W will get fused if it is made to consume 150 W or more. What voltage fluctuation will the bulb withstand?
Given that the operating voltage is V and power consumed is P.
Therefore, the resistance of the bulb,
The power fluctuation, p = 150 W. So, the voltage fluctuation that the bulb can withstand,
The bulb will withstand up to 270 V.
Q.9. An immersion heater rated 1000 W, 220 V is used to heat 0.01 m3 of water. Assuming that the power is supplied at 220 V and 60% of the power supplied is used to heat the water, how long will it take to increase the temperature of the water from 15°C to 40°C?
Given the operating voltage V and power consumed P, the resistance of the immersion heater,
Mass of water,
Specific heat of water, s = 4200 Jkg-1K-1
Rise in temperature, θ = 25°C
Heat required to raise the temperature of the given mass of water,
Q = msθ = 10 × 4200 × 25 = 1050000 J
Let t be the time taken to increase the temperature of water. The heat liberated is only 60%. So,
⇒ t = 29.17 minutes
Q.10. An electric kettle used to prepare tea, takes 2 minutes to boil 4 cups of water (1 cup contains 200 cc of water) if the room temperature is 25°C. (a) If the cost of power consumption is Re 1.00 per unit (1 unit = 1000 watt-hour), calculate the cost of boiling 4 cups of water. (b) What will be the corresponding cost if the room temperature drops to 5°C?
Time taken to boil 4 cups of water, t = 2 minutes
Volume of water boiled = 4 × 200 cc = 800 cc
Initial temperature, θ1 = 25°C
Final temperature, θ2 = 100°C
Change in temperature, θ = θ2 − θ1 = 75°C
Mass of water to be boiled, m = 800 × 1 = 800 gm = 0.8 Kg
Heat required for boiling water,
Q = msθ = 0.8 × 4200 × 75 = 252000 J
We know:-
1000 watt - hour = 1000 × 3600 watt sec.
∴ Cost of boiling 4 cups of water
= Rs. 0.7
(b) Initial temperature, θ1 = 5°C
Final temperature, θ2 = 100°C
Change in temperature, θ = θ2 − θ1 = 95°C
Q = msθ = 0.8 × 4200 × 95 = 319200
∴ Cost of boiling 4 cups of water
= Rs. 0.09
Q.11. The coil of an electric bulb takes 40 watts to start glowing. If more than 40 W are supplied, 60% of the extra power is converted into light and the remaining into heat. The bulb consumes 100 W at 220 V. Find the percentage drop in the light intensity at a point if the supply voltage changes from 220 V to 200 V.
Case-I : When the supply voltage is 220 V.
Power consumed by the bulb = 100 W
Excess power = 100 − 40 = 60 W
Power converted to light = 60% of 60 W = 36 W
Case-II : When the supply voltage is 200 V.
Power consumed =
Excess power = 82.64 − 40 = 42.64 W
Power converted to light = 60% of 42.64 W = 25.584 W
Percentage drop in light intensity,
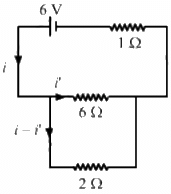
Q.12. The 2.0 Ω resistor shown in the figure is dipped into a calorimeter containing water. The heat capacity of the calorimeter together with water is 2000 J K−1. (a) If the circuit is active for 15 minutes, what would be the rise in the temperature of the water? (b) Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?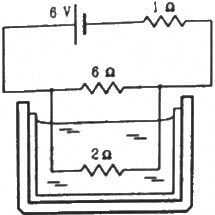
The effective resistance of the circuit,
Current i through the circuit,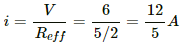
Let i' be the current through the 6 Ω resistor. Then,
i' × 6 = (i − i') × 2
(a) Heat generated in the 2 Ω resistor,
H = (i - i')2Rt
The heat capacity of the calorimeter together with water is 2000 J K−1. Thus, 2000 J of heat raise the temp by 1 K.
∴ 5832 J of heat raises the temperature by
(b) When the 6 Ω resistor gets burnt, the effective resistance of the circuit,
Reff = 1 + 2 = 3 Ω
Current through the circuit,
i = 6/3 = 2A
Heat generated in the 2 Ω resistor = (2)2× 2 × 15 × 60 = 7200 J
2000 J raise the temperature by 1 K.
∴ 7200 J raise the temperature by
7200/2000 = 3.6K
Q.13. The temperatures of the junctions of a bismuth-silver thermocouple are maintained at 0°C and 0.001°C. Find the thermo-emf (Seebeck emf) developed. For bismuth-silver, a = − 46 × 10−6 V°C−1 and b = −0.48 × 10−6 V°C−2.
Given:-
Difference in temperature, θ = 0.001°C,
a = − 46 × 10−6 V °C−1
b = − 0.48 × 10−5 V °C−2
= − 46 × 10−9 − 0.24 × 10−12
= − 46.0024 × 10−9
= − 4.6 × 10−8 V
Q.14. Find the thermo-emf developed in a copper-silver thermocouple when the junctions are kept at 0°C and 40°C. Use the data given in the following table.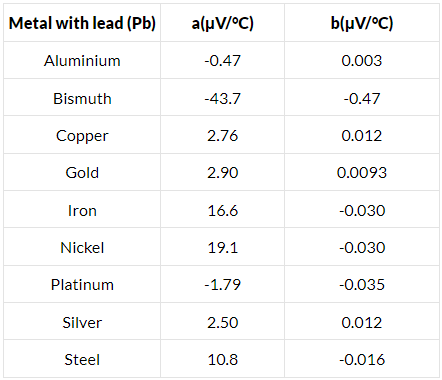
Difference in temperature, θ = 40°C
acs = [2.76 − (−43.7) μV
= 46.46 μV/°C
bcs = [0.012 − (−0.47) μV/°C
= 0.482 μV/°C2
Putting this value in eq. (1), we get:-
Ecs = 46.46 × 10−6 × 40 + (1/2)× 0.482 × 10−6 × (40)2
= 1.04 × 10−5 V
Q.15. Find the neutral temperature and inversion temperature of a copper-iron thermocouple if the reference junction is kept at 0°C. Use the data given in the following table.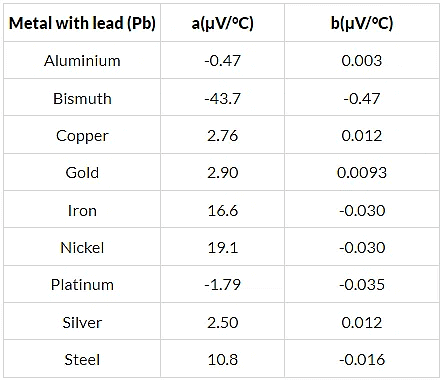
Neutral temperature,
Thus, the neutral temperature,
The inversion temperature is double the neutral temperature, i.e. 659 °C.
Q.16. Find the charge required to flow through an electrolyte to liberate one atom of (a) a monovalent material and (b) a divalent material.
(a) Amount of charge required by 1 equivalent mass of the substance = 96500 C
For a monovalent material, equivalent mass = molecular mass
⇒ Amount of charge required by 6.023 × 1023 atoms = 96500 C
∴ Amount of charge required by 1 atom =
(b) For a divalent material, equivalent mass = 1/2 molecular mass
⇒ Amount of charge required by
∴ Amount of charge required by 1 atom = 1.6 × 2 × 10−19 = 3.2 × 10−19 C
Q.17. Find the amount of silver liberated at the cathode if 0.500 A of current is passed through an AgNO3 electrolyte for 1 hour. Atomic weight of silver is 107.9 g mol−1.
Equivalent mass of silver, EAg = 107.9 g.............(∵ Ag is monoatomic)
The ECE of silver,
Using the formula, m = Zit, we get:-
m = 0.00118 × 0.500 × 3600
= 2.01 g
So, 2.01 g of silver is liberated.
Q.18. An electroplating unit plates 3.0 g of silver on a brass plate in 3.0 minutes. Find the current used by the unit. The electrochemical equivalent of silver is 1.12 × 10−6 kg C−1.
Given:-
Mass of silver deposited, m = 3 g
Time taken, t = 3 min. = 180 s
E.C.E. of silver, Z = 1.12 × 10−6 kg C−1
Using the formula, m = Zit, we get:-
Q.19. Find the time required to liberate 1.0 litre of hydrogen at STP in an electrolytic cell by a current of 5.0 A.
Let the required time be t.
Mass of 1 litre hydrogen,
m = 2/22.4g
Using the formula, m = Zit, we get:-
Q.20. Two voltameters, one with a solution of silver salt and the other with a trivalent-metal salt, are connected in series and a current of 2 A is maintained for 1.50 hours. It is found that 1.00 g of the trivalent metal is deposited.
(a) What is the atomic weight of the trivalent metal?
(b) How much silver is deposited during this period? Atomic weight of silver is 107.9 g mol−1.
Given:-
Mass of salt deposited, m = 1 g
Current, i = 2 A
Time, t = 1.5 hours = 5400 s
For the trivalent metal salt:-
Equivalent mass = 1/3 Atomic weight
The E.C.E of the salt,
(b) Using the relation between equivalent mass and mass deposited on plates, we get:-
Q.21. A brass plate of surface area 200 cm2 on one side is electroplated with 0.10 mm thick silver layers on both sides using a 15 A current. Find the time taken to do the job. The specific gravity of silver is 10.5 and its atomic weight is 107.9 g/mol−1.
Given:-
Current, i = 15 A
Surface area of the plate = 200 cm2,
Thickness of silver deposited= 0.1 mm = 0.01 cm
Volume of Ag deposited on one side = 200 × 0.01 cm3 = 2 cm3
∴ Volume of Ag deposited on both side = 4 cm3
Mass of silver deposited,
m = Volume × Specific gravity × 1000 = 4 × 10-3 × 10.5 ×1000 = 42 kg
Using the formula, m = Zit, we get:-
42 = ZAg × 15 × t
Q.22. The figure shows an electrolyte of AgCl through which a current is passed. It is observed that 2.68 g of silver is deposited in 10 minutes on the cathode. Find the heat developed in the 20 Ω resistor during this period. Atomic weight of silver is 107.9 g/mol−1.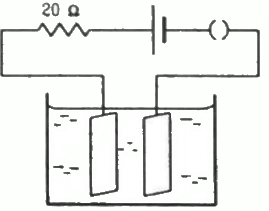
Given:-
Mass of silver deposited, m = 2.68 g
Time, t = 10 minutes = 600 s
Using the formula, m = Zit, we get:-
Heat developed in the 20 Ω resistor,
Q.23. The potential difference across the terminals of a battery of emf 12 V and internal resistance 2 Ω drops to 10 V when it is connected to a silver voltameter. Find the silver deposited at the cathode in half an hour. Atomic weight of silver is 107.9 g mol−1.
Let i be the current through the circuit.
Emf of battery, E = 12 V
Voltage drop across the voltameter, V = 10 V
Internal resistance of the battery, r = 2 Ω
Applying Kirchoff's Law in the circuit, we get:-
Using the formula m = Zit, we get:-
Q.24. A plate of area 10 cm2 is to be electroplated with copper (density 9000 kg m−3) to a thickness of 10 micrometres on both sides, using a cell of 12 V. Calculate the energy spent by the cell in the process of deposition. If this energy is used to heat 100 g of water, calculate the rise in the temperature of the water. ECE of copper = 3 × 10−7 kg C−1 and specific heat capacity of water = 4200 J kg−1.
Surface area of the plate, A = 10 cm2 = 10 × 10−4 m2
Thickness of copper deposited, t = 10 μm = 10−5 m
Density of copper = 9000 kg/m3
Volume of copper deposited, V = A(2t)
V = 10 × 10−4 × 2 × 10 × 10−6
= 2 × 102 × 10−10
= 2 × 10−8 m3
Mass of copper deposited, m = Volume × Density = 2 × 10−8 × 9000
⇒ m = 18 × 10−5 kg
Using the formula, m = ZQ, we get:-
18 × 10−5 = 3 × 10−7 × Q
⇒ Q = 6 × 102 C
Energy spent by the cell = Work done by the cell
⇒W = VQ
= 12 × 6 × 102
= 72 × 102 = 7.2 kJ
Let ∆θ be the rise in temperature of water. When this energy is used to heat 100 g of water, we have:-
7.2 × 103 = 100 × 10−3 × 4200 × ∆θ
⇒ ∆θ = 17 K
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 33: Thermal and Chemical Effects of Current- 2 - HC Verma Solutions - JEE
| 1. What are the thermal effects of current? |  |
| 2. How is the heat produced in a wire when current flows through it? |  |
| 3. What is the relationship between current and temperature in a wire? |  |
| 4. How does the thermal effect of current affect the efficiency of an electrical device? |  |
| 5. What are the safety measures to be taken to prevent thermal effects in electrical circuits? |  |