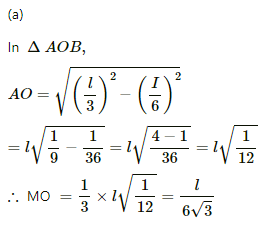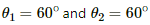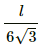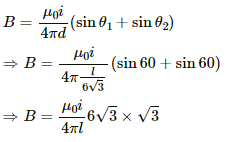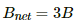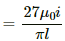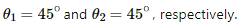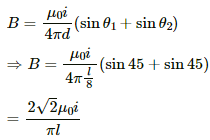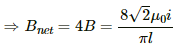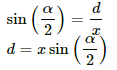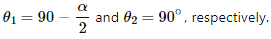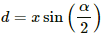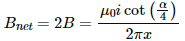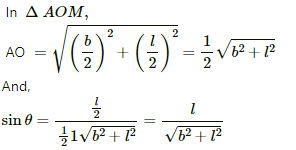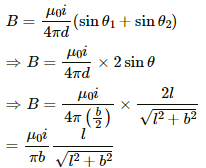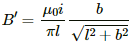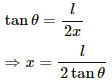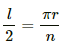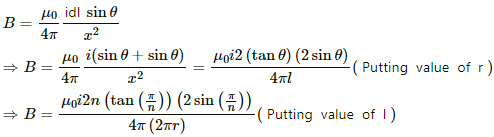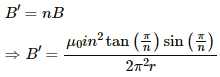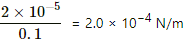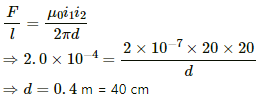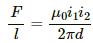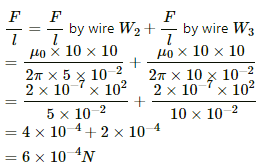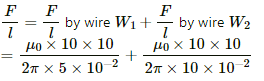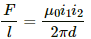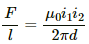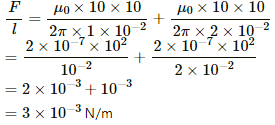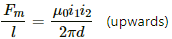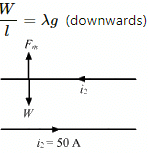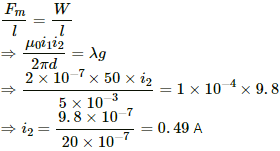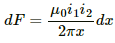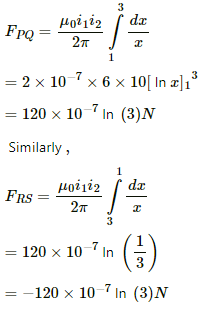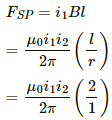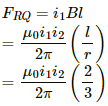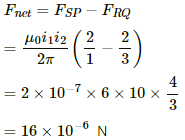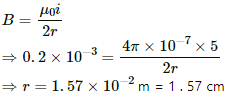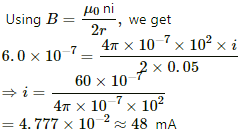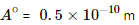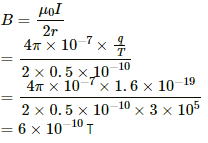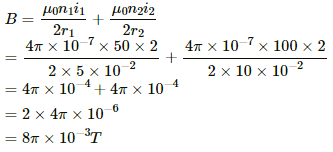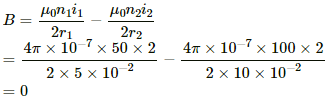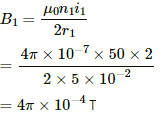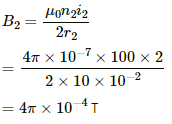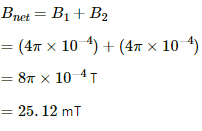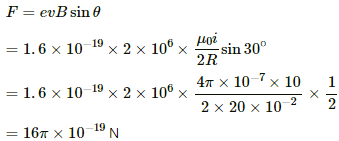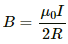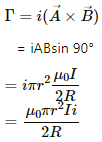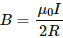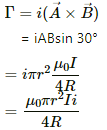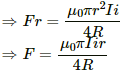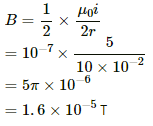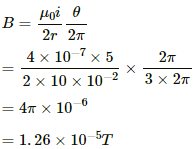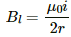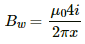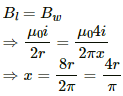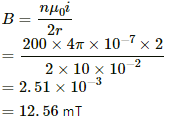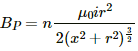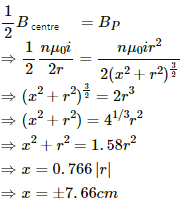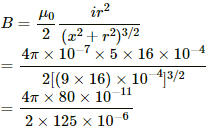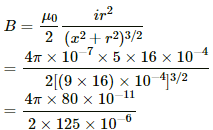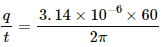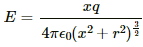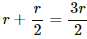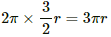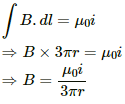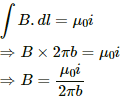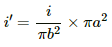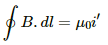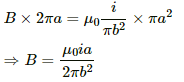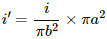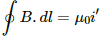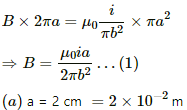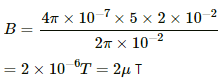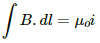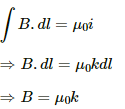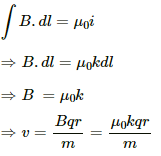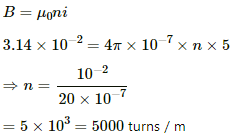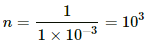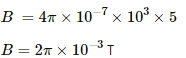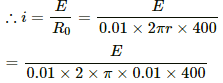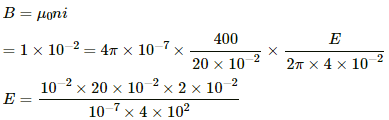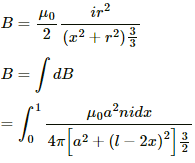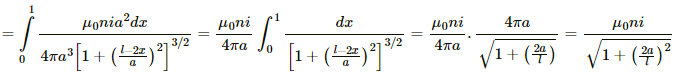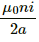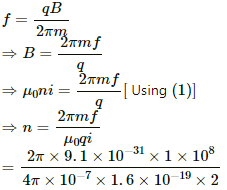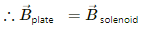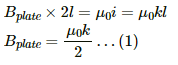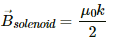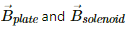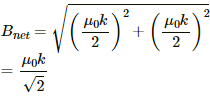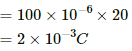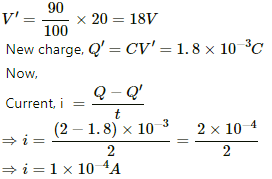HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 3 | HC Verma Solutions - JEE PDF Download
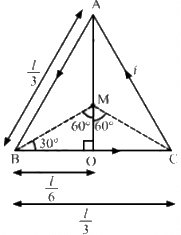
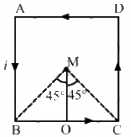
Q.21. A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
Let ABC be the equilateral triangle with side l/3 and centre M.
The angles made by points B and C with centre M are
Separation of the point from the wire, d = MO =
Thus, the magnetic field due to current in wire BC is given by
Now,
Net magnetic field at M = Magnetic field due to wire BC + Magnetic field due to wire CA + Magnetic field due to wire AB
Since all wires are the same
It is perpendicular to the plane in outward direction if the current is anticlockwise and perpendicular to the plane in inward direction if the current is clockwise.
(b)
The angles made by points B and C with centre M are
Separation of the point from the wire, d = l/8
Thus, the magnetic field due to current in wire BC is given by
Since all wires are the same,
Net magnetic field at M = 4 × Magnetic field due to wire BC
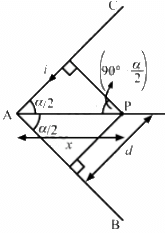
Q.22. A long wire carrying a current i is bent to form a place along α . Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
Let CAB be the wire making an angle α, P be the point on the bisector of this angle situated at a distance x from the vertex A and d be the perpendicular distance of AC and AB from P.
From the figure,
The angles made by points A and C with point P are
Separation of the point from the wire,
Thus, the magnetic field due to current in wire AC is given by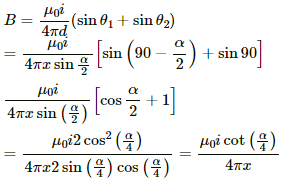
Now, the magnetic field due to wires AC and AB is given by
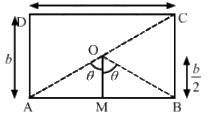
Q.23. Find the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
Let the angles made by points A and B with point O be θ1 and θ2, respectively.
And,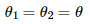
Separation of the point from the wire, d = b/2
Thus, the magnetic field due to current in wire AB is given by
Similarly, the magnetic field due to current in wire BC is given by
Now,
Magnetic field due to current in wire CD = Magnetic field due to current in wire AB = B
And,
Magnetic field due to current in wire DA = Magnetic field due to current in wire BC = B'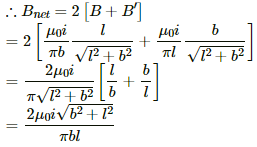
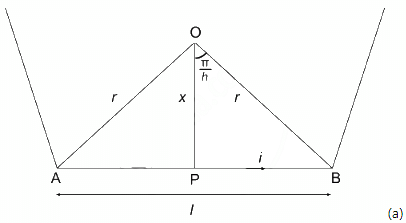
Q.24. A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
Using figure,
For a regure polygon of n - sides, the angle subtended at the centre is 2π/n.considering angle to be small
Using Biot - Savart law for one side
For n - sided polygon
(b) when n→ ∞, polygon becomes a circle with radius r and magnetic field will become
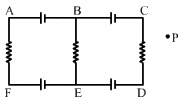
Q.25. Each of the batteries shown in figure has an emf equal to 5 V. Show that the magnetic field B at the point P is zero for any set of values of the resistances.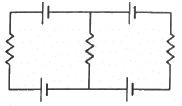
By appluing Kirchoff voltage law, we can see that the current in the circuit is zero.
Net current in the circuit = 0
As magnetic field is always proportional to the current flowing in the circuit hence,
Net magnetic field at point P = 0
Field at point P is independent of the values of the resistances in the circuit.
Q.26. A straight, how wire carries a current of 20 A. Another wire carrying equal current is placed parallel to it. If the force acting on a length of 10 cm of the second wire is 2.0 × 10−5 N, what is the separation between them?
Given:
Magnitude of current in both wires, i1 = i2 = 20 A
Force acting on 0.1 m of the second wire, F = 2.0 × 10−5 N
∴ Force per unit length =
Now,
Let the separation between the two wires be d.
Thus, the force per unit length is given by
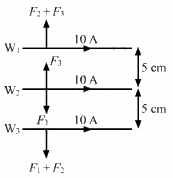
Q.27. Three coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
Let wires W1, W2 and W3 be arranged as shown in the figure.
Given:
Magnitude of current in each wire, i1 = i2 = i3 = 10 A
The magnetic force per unit length on a wire due to a parallel current-carrying wire is given by
So, for wire W1,
For wire W2,
For wire W3,
= 6 × 10−4 N
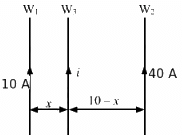
Q.28. Two parallel wires separated by a distance of 10 cm carry currents of 10 A and 40 A along the same direction. Where should a third current by placed so that it experiences no magnetic force?
Let the third wire W3 having current i in upward direction be placed x cm from the 10 A current wire.
The magnetic force per unit length on a wire due to a parallel current-carrying wire is given by
According to the question, wire W3 experiences no magnetic force.
Thus, wire W3 is placed 2 cm from the 10 A current wire.
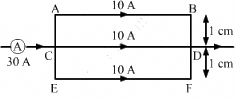
Q.29. Figure shows a part of an electric circuit. The wires AB, CD and EF are long and have identical resistance. The separation between the neighbouring wires is 1.0 cm. The wires AE and BF have negligible resistance and the ammeter reads 30 A. Calculate the magnetic force per unit length of AB and CD.
Since wires AB, CD and EF have identical resistance, the current (30 A) gets equally distributed in them, that is, 10 A in each wire.
The magnetic force per unit length on a wire due to a parallel current-carrying wire is given by
∴ Magnetic force per unit length of AB = Force due to current in CD + Force due to current in EF
Similarly,
Magnetic force per unit length of CD = Force due to current in AB − Force due to current in EF
∵ Force on CD due to current in AB = Force due to current in EF
∴ Magnetic force per unit length of CD = 0
Q.30. A long, straight wire is fixed horizontally and carries a current of 50.0 A. A second wire having linear mass density 1.0 × 10−4 kg m−1 is placed parallel to and directly above this wire at a separation of 5.0 mm. What current should this second wire carry such that the magnetic repulsion can balance its weight?
Given:
Magnitude of current, i1 = 10 A
Separation between two wires, d = 5 mm
Linear mass density of the second wire, λ = 1.0 × 10−4 kgm−1
Now,
Let i2 be the current in the second wire in opposite direction.
Thus, the magnetic force per unit length on the wire due to a parallel current-carrying wire is given by
Also,
Weight of the second wire, W = mg
Weight per unit length of the second wire,
Now, according to the question,
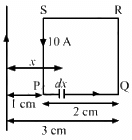
Q.31. A square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure. (a) Show that the magnetic force acting on the part PQ is equal and opposite to the part RS. (b) Find the magnetic force on the square loop.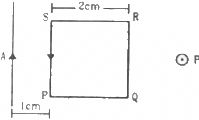
Given:
Current in the loop, i1 = 6 A
Current in the wire, i2 = 10 A
Now, consider an element on PQ of width dx at a distance x from the wire.
Force on the element is given by
Force acting on part PQ is given by
Both forces are equal in magnitude, but they are opposite in direction.
(b) The magnetic field intensity due to wire on SP is given by
Force on part SP is given by
(Towards right)
Force on part RQ is given by
(Towards left)
Thus, the net force on the loop is given by
(Towards right)
Q.32. A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
Given:
No. of turns, n = 1
Magnitude of current, i = 5.00 A
Now, let the radius of the loop be r.
Thus, the magnetic field at the centre due to the current in the loop is given by
Q.33. A current-carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of 6.0 × 10−5 T at its centre. Find the value of the current.
Given:
No. of turns, n = 100
Radius of the loop, r = 5 cm = 0.05 m
Magnetic field intensity, B = 6.0 × 10−5 T
Now, let the magnitude of current be i.
Q.34. An electron makes 3 × 105 revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
Given:
Frequency of the electron = 3 × 105
Time taken by the electron to complete one revolution, T = 1/Frequency
Current in the circle, i = q/t
Radius of the loop, r = 0.5
Thus, the magnetic field at the centre due to the current in the loop is given by
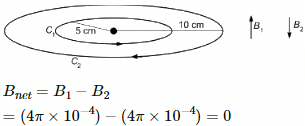
Q.35. A conducting circular loop of radius a is connected to two long, straight wires. The straight wires carry a current i as shown in figure. Find the magnetic field B at the centre of the loop.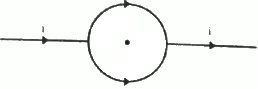
As the centre of the loop, that is, point O, lies on the same line of two long, straight wires, the magnetic field at O due to each straight wire is zero.
Since wires ABC and ADC are identical, the current gets equally distributed in two parts at point A. So, the magnetic field due to ABC and ADC at O are equal in magnitude but are opposite in directions. (as shown in the figure).
∴ Net magnetic field at O = 0
Q.36. Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
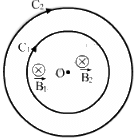
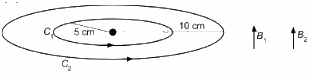
No. of turns: n1 = 50 and n2 = 100
Magnitude of currents: i1 = i2 = 2 A
Radii of loops: r1 = 5 cm and r2 = 10 cm
(a) In the same sense:
The magnetic field intensity at the centre is given by
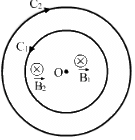
(b) In the opposite sense:
The magnetic field intensity at the centre is given by
Q.37. Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. If the outer coil is rotated through 90° about a diameter, Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
Given:-
No. of turns: n1 = 50 and n2 = 100
Magnitude of currents: i1 = i2 = 2 A
Radii of loops: r1 = 5 cm and r2 = 10 cm
(a) In the same sense:-
The magnetic field intensity at the centre due to C1 is given by
(In the plane of paper in upward direction)
The magnetic field intensity at the centre due to C2 is given by
(In the plane of paper in upward direction)
In this case, magnetic fields due to C1 and C2 at the centre are along the same direction.
Thus, the net magnetic field is given by
(b) When the direction of current in the two coils is opposite to each other then the magnetic fields will also point in opposite directions as shown in the figure. Hence, the net magnetic field will be obtained by the subtraction of the two magnetic fields.
Q.38. A circular loop of radius 20 cm carries a current of 10 A. An electron crosses the plane of the loop with a speed of 2.0 × 106 m s−1. The direction of motion makes an angle of 30° with the axis of the circle and passes through its centre. Find the magnitude of the magnetic force on the electron at the instant it crosses the plane.
Given:
Magnitude of current in the loop, I = 10 A
Radius of the loop, r = 20 cm = 20 × 10−2 m
Thus, the magnetic field intensity at the centre is given by
Now,
Velocity of the electron, v = 2 × 106 m/s
Angle between the velocity and the magnetic field intensity, θ = 30°
Thus, the magnetic force on the electron is given by
Q.39. A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
Given:
For the outer loop,
Magnitude of current = I
Radius of the loop = R
Thus, the magnetic field at the centre due to the larger loop is given by
Let A be the area of the smaller loop and let current i pass through it.
Now,
Angle between the area vector of the smaller loop and the magnetic field due to the larger loop = 90°
Thus, the required torque is given by
Q.40. A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>>r) carrying a current I. The plane of the smaller loop makes an angle of 30° with that of the larger loop. If the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
Given:
For the outer loop,
Magnitude of current = I
Radius of the loop = R
Thus, the magnetic field at the centre due to the larger loop is given by
Let A be the area of the smaller loop and let current i pass through it.
Now,
Angle between the area vector of the smaller loop and the magnetic field due to the larger loop = 30°
Thus, the torque on the smaller loop is given by
If the smaller loop is held fixed in its position, then
Torque due to the magnetic field = Torque due to the external force at its periphery
This is the minimum magnitude of force to balance the given condition.
Q.41. Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
Given:
Magnitude of current, I = 5 A
Radius of the semi-circular wire, r = 10 cm
∴ Required magnetic field at the centre of curvature
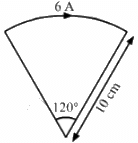
Q.42. A piece of wire carrying a current of 6.00 A is bent in the form of a circular are of radius 10.0 cm, and it subtends an angle of 120° at the centre. Find the magnetic field B due to this piece of wire at the centre.
Given:
Magnitude of current, I = 6 A
Radius of the semi-circular wire, r = 10 cm
Angle subtended at the centre, θ = 120° = 2π/3
∴ Required magnetic field at the centre of curvature
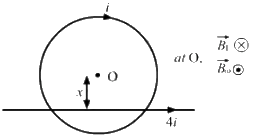
Q.43. A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
Given:
Magnitude of current = i
Radius of the loop = r
Magnetic field due to the loop at its centre,
Let a straight wire carrying 4 i current be placed at a distance x from the centre such that the magnetic fields of the loop and the wire are of equal magnitude but in opposite direction at O.
Magnetic field due to the wire at the centre of the loop,
According to the question,
This means that the wire is placed 4r/π from the centre of the loop (as shown in the figure).
Q.44. A circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field 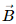 at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?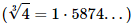
Number of turns, n = 200
Radius of the coil, r = 10 cm
Current in the coil, i = 2A
(a) Let the magnetic field at the centre of the coil is B.
As the relation for magnetic field at the centre of a circular coil is given by
(b) As magnetic field at any point P (say) on the axis of the circular coil is given by
Where x is the distance of the point from the centre of the coil.
As per the question
Magnetic field will drop to half of its value at the centre if the distance of that point from the centre of the coil along the axis of coil is equal to 7.66 cm.
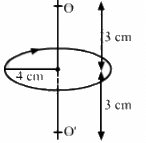
Q.45. A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
Given:
Magnitude of current, I = 5.0 A
Radius of the loop, r = 4.0 cm
(a) The magnetic field intensity B on point O at a distance x on the axial line is given by
= 4.019 x 10-5 T (in downward direction)
(b) The magnetic field intensity B on point O' at a distance x on the axial line is given by
= 4.019 x 10-5 T (in downward direction)
Q.46. A charge of 3.14 × 10−6 C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s−1. Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
Given:
Magnitude of charges, q = 3.14 × 10−6 C
Radius of the ring,
r = 20 cm = 20 x 10-2 m
Angular velocity of the ring
ω = 60 rad/s
Time for 1 revolution = 2π/60
∴ Current, i =
= 30 x 10-6 A
In the figure, E1 and E2 denotes the electric field at a point on the axis at a distance of 5.00 cm from the centre due to small element 1 and 2 of the ring respectively.
E is the resultant electric field due to the entire ring at a point on the axis at a distance of 5.00 cm from the centre.
The electric field at a point on the axis at a distance x from the centre is given by
The magnetic field at a point on the axis at a distance x from the centre is given by
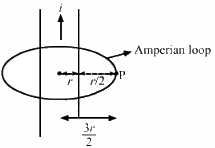
Q.47. A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
(a) The magnetic field inside any conducting tube is always zero.
∴ Magnetic field inside the tube at a distance r/2 from the surface = 0
(b) Let the point outside the tube with distance r/2 be P.
∴ Net distance from centre, r' =
Consider an Amperian loop, as shown in the figure.
Length of the loop, l =
Current enclosed in the loop = i
On applying Ampere's law, we get
Q.48. A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
(a) The magnetic field inside any conducting tube is always zero.
∴ Magnetic field just inside the tube is zero.
(b) Let the point outside the tube with distance b be P.
Consider an Amperian loop, as shown in the figure.
Length of the loop, l = 2π x b = 2πb
Current enclosed in the loop = i
On applying Ampere's law, we get
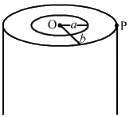
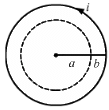
Q.49. A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
Given:
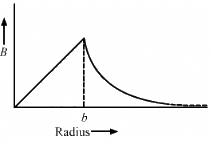
Magnitude of current = i
Radius of the wire = b
For a point at a distance a from the axis,
Current enclosed,
By Ampere's circuital law,
For the given conditions,
Q.50. A solid wire of radius 10 cm carries a current of 5.0 A distributed uniformly over its cross section. Find the magnetic field B at a point at a distance (a) 2 cm (b) 10 cm and (c) 20 cm away from the axis. Sketch a graph B versus x for 0 < x < 20 cm.
Given:
Magnitude of current, i = 5 A
Radius of the wire, b = 10 cm = 10 x 10-2 m
For a point at a distance a from the axis,
Current enclosed,
By Ampere's circuital law,
For the given conditions,
Again, using the circuital law, we get
(b) On putting a = 10 cm = 10 x 10-2 m in (1), we get
B = 10 μT
(c)Using the circuital law, we get
Q.51. Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.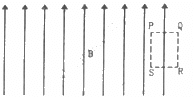
Half of the loop PQRS is in the region of magnetic field and half in the area of zero magnetic field.
Let us consider a current carrying circular wire, due to which there is uniform magnetic field in the region.
Take a point A inside the loop PQRS in the region where B = 0
According to Ampere's circuital law,
If there is current enclosed by the loop PQRS, then magnetic field B cannot be 0.
Whereas, we have taken the magnetic field at point A to be zero.
Thus, such a field is not possible.
Q.52. Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.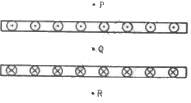
At point P,
Current, i = 0
∴ Magnetic field B = 0
At point Q,
Applying Ampere's law, we get
At point R,
Current, i = 0
∴ B = 0
Q.53. Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
Given:
Charge = q
Mass = m
Radius = r
We know that the radius described by a charged particle in a magnetic field is given by
r = mv/qB
Using Ampere circuital law
Q.54. The magnetic field B inside a long solenoid, carrying a current of 5.00 A, is 3.14 × 10−2 T. Find the number of turns per unit length of the solenoid.
Given:
Magnitude of current, i = 5 A
Magnetic field intensity, B = 3.14 × 10−2 T
We know that the magnetic field inside a long solenoid having n turns per unit length is given by
Q.55. A long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
Given:
Radius of the wire, r = 0.5 mm
Width of each turn, = diameter of the wire, 2r = 1 mm = 1 × 10−3 m
∴ Total number of turns in 1 m solenoid
Magnitute of current , i = 5 A
Using B = μ0ni, We get
Q.56. A copper wire having resistance 0.01 ohm in each metre is used to wind a 400-turn solenoid of radius 1.0 cm and length 20 cm. Find the emf of a battery which when connected across the solenoid will cause a magnetic field of 1.0 × 10−2 T near the centre of the solenoid.
Given:
Resistance per unit length of the wire, R/l = 0.01 Ω/m
Radius of the wire, r = 1.0 cm = 0.01 m
Total no. of turns, N = 400
Magnetic field intensity, B = 1.0 × 10−2 T
Now,
Let E be the emf of the battery and R0 be the total resistance of the wire.
The magnetic field near the centre of the solenoid is given by
= 1 V
Q.57. A tightly-wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current i n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) verify that if l >> a, the field tends to B = µ0ni and if a >> l, the field tends to 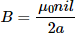 . Interpret these results.
. Interpret these results.
(a) Given:
Current in the loop or circular current = indx
Radius of the loop having circular current = r
Distance of the centre of the solenoid from the circular current = (l/2) - x
Magnetic field at the centre due to the circular loop,
(b) When a > > l, B =
Q.58. A tightly-wound, long solenoid carries a current of 2.00 A. An electron is found to execute a uniform circular motion inside the solenoid with a frequency of 1.00 × 108 rev s−1. Find the number of turns per metre in the solenoid.
Given:
Magnitude of current in the solenoid, i = 2 A
Frequency of the electron, f = 1 x 108 rev/s
Mass of the electron, m = 9.1 x 10-31 kg
Charge of the electron, q = 1.6 x 10-19 C
We know that the magnetic field inside a solenoid is given by
B = µ0ni
If a particle executes uniform circular motion inside a magnetic field, the frequency of the particle is given by
= 1420 turns/m
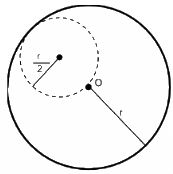
Q.59. A tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
Given:
Magnitude of current in the solenoid = i
Number of turns per unit length = n
When a particle is projected perpendicular to the magnetic field, it describes a circular path.
And for the particle (projected from a point on the axis in a direction perpendicular to the axis) to not strike the solenoid, the maximum radius of that circular path should be r/2.
∴ Radius of the circle = r/2.
O is a point on the axis of the solenoid . The magnetic field of the solenoid is along the axis, Which is perpendicular to the plane of paper.
We know,
Centripetal force = Magnetic force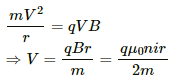
Q.60. A tightly-wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surface current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) Find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
Given:
Number of turns per unit length of the solenoid = n
(a) Since the net magnetic field near the centre of the solenoid is 0,
Using Guass's law for the plate, we get
For the solenoid,...(2)
From (1) and (2), we get i = k/2n
(b) On putting the value of n in (2), we get
Now,
are perpendicular to each other.
Thus, the net magnetic field near the centre of the solenoid is given by
Q.61. A capacitor of capacitance 100 µF is connected to a battery of 20 volts for a long time and then disconnected from it. It is now connected across a long solenoid having 4000 turns per metre. It is found that the potential difference across the capacitor drops to 90% of its maximum value in 2.0 seconds. Estimate the average magnetic field produced at the centre of the solenoid during this period.
Given:
Capacitance, C = 100 microfarad
Voltage, V = 20 V
Charge stored in the capacitor, Q = CV
It is given that the potential difference across the capacitor drops to 90% of its maximum value.
Thus,
No. of turns per metre, n = 4000
Thus, the average magnetic field at the centre of the solenoid is given by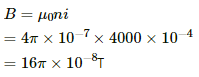
|
134 docs
|