Short Answers
Q.1. You are driving a motorcycle on a horizontal road. It is moving with a uniform velocity. Is it possible to accelerate the motorcycle without putting higher petrol input rate into the engine?
Yes, it is possible to accelerate the motorcycle without putting higher petrol input rate into the engine by driving the motorcycle on a circular track.
Q.2. Some washing machines have cloth driers. It contains a drum in which wet clothes are kept. As the drum rotates, the water particles get separated from the cloth. The general description of this action is that "the centrifugal force throws the water particles away from the drum". Comment on this statement from the viewpoint of an observer rotating with the drum and the observer who is washing the clothes.
The person rotating with the drum will observe that centrifugal force and coriolis force act on the water particles and the person washing the cloth will observe that water particles are thrown outward (away from the drum) and no pseudo force is acting on the particles.
Q.3. A small coin is placed on a record rotating at 33(1/3) rev/minute. The coin does not slip on the record. Where does it get the required centripetal force from?
The coin gets the required centripetal force from the frictional force between the coin and the record.
Q.4. A bird while flying takes a left turn, where does it get the centripetal force from?
The bird tilts its body and tail in such a way that the air around offers a dragging force in left direction, perpendicular to its initial direction of motion. This dragging force provides the necessary centripetal force to take the left turn.
Q.5. Is it necessary to express all angles in radian while using the equation ω = ω0 + at ?
No, it is not necessary to express all the angles in radian while using the equation ω = ω0 + at.
If ω (angular velocity) and α (angular acceleration) are in rad/s and rad/s2, respectively, we will get the angle in radian.
Q.6. After a good meal at a party you wash your hands and find that you have forgotten to bring your handkerchief. You shake your hand vigorously to remove the water as much as you can. Why is water removed in this process?
While shaking, our hand moves on a curved path with some angular velocity and water on our hand feels centrifugal force in the outward direction. Therefore, water get detached from our hand and leaves it.
Q.7. A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
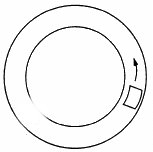
The outer wall will exert a non-zero normal contact force on the block. As the block moves in a uniform circular motion, centrifugal force in radially outward direction acts on it and it comes in contact with the outer wall of the tube.
Q.8. Consider the circular motion of the earth around the sun. Which of the following statements is more appropriate?
(a) Gravitational attraction of the sun on the earth is equal to the centripetal force.
(b) Gravitational attraction of the sun on the earth is the centripetal force.
(a) Gravitational attraction of the Sun on the Earth is equal to the centripetal force. This statement is more appropriate.
Gravitational attraction of the Sun on the Earth provides the necessary centripetal force required for the circular motion of the Earth around the Sun.
Q.9. A car driver going at some speed v suddenly finds a wide wall at a distance r. Should he apply brakes or turn the car in a circle of radius r to avoid hitting the wall?
As the wall is at a distance r, the driver should either take a circular turn of radius r or apply brakes to avoid hitting the wall.
Q.10. A heavy mass m is hanging from a string in equilibrium without breaking it. When this same mass is set into oscillation, the string breaks. Explain.
When the same mass is set into oscillation, the tension in the string increases because of the additional centripetal force of the mass oscillating in a curved path.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:When a particle moves in a circle with a uniform speed
Explanation
In a circular motion, the direction of particle changes. Therefore, velocity, being a vector quantity, also changes. As the velocity changes, acceleration also changes.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:Tow cars having masses m1 and m2 moves in circles of radii r1 and r2 respectively. If they complete the circle in equal time, the ratio of their angular speed ω1/ω2 is
Explanation
Time period (T) is same for both the cars.
We know that :
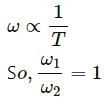
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.

Explanation
From the figure in the question, it is clear that rB > rA.
Here, normal reaction is inversely proportional to the centrifugal force acting on the car, while taking turn on the curve track. Also, centrifugal force is inversely proportional to the radius of the circular track.
Therefore, we have: NA < NB
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centrifugal force on it is
Explanation
The centrifugal force is a pseudo force and can only be observed from the frame of reference, which is non-inertial w.r.t. the particle.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A particle of mass m rotates with a uniform angular speed ω. It is viewed from a frame rotating about the Z-axis with a uniform angular speed ω0. The centrifugal force on the particle is
Explanation
The centrifugal force on the particle depends on the angular speed (ω0) of the frame and not on the angular speed (ω) of the particle. Thus, the value of centrifugal force on the particle is 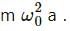
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
Explanation
It is given that the turntable is rotating with uniform angular velocity. Let the velocity be ω.
We have:
v = rω
⇒ v ∝ r (P for constant ω)
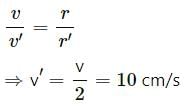
Similarly, we have: 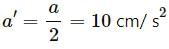
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
Explanation
At the top of the path, the direction of mg is vertically downward and for centrifugal force (mv2/r), the direction is vertically upward. If the vertically downward force is not greater, water will not fall.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
Explanation
The stone will move in a circle and the direction of velocity at any instant is always along the tangent at that point. Therefore, the stone will move along the tangent to the circle at a point where the string breaks.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
Explanation
Let the force of friction between the coin and the rotating turntable be F.
For the coin to just slip ,
we have : F = mω2r
Here, mω2r is the centrifugal force acting on the coin.
For constant F and m, we have : 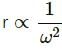
Therefore,
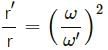
⇒ r' = 1 cm
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
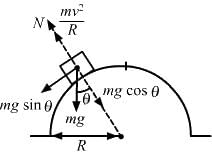
Try yourself:A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
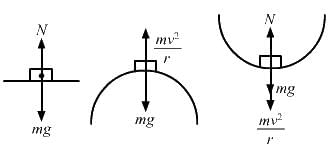
Try yourself:Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
Explanation
FC is maximum of the three forces.
At the middle of bridge, normal force can be given as : NA = mg
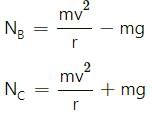
So, FC is maximum.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:If the earth stop rotating, the apparent value of g on its surface will
Explanation
If the Earth stops rotating on its axis, there will be an increase in the value of acceleration due to gravity at the equator. At the same time, there will be no change in the value of g at the poles.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
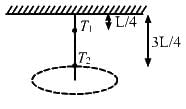
Try yourself:A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
Explanation
When the car is in air, the acceleration of bob and car is same. Hence, the tension in the string will be zero.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
Explanation
Tension is the string, 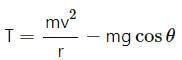
When v = 0,
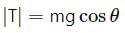
That is, at the extreme positions, the tension is the string is mgcosθ.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:An object follows a curved path. The following quantities may remain constant during the motion
Explanation
When an object follows a curved path, its direction changes continuously. So, the scalar quantities like speed and magnitude of acceleration may remain constant during the motion.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
Explanation
The speed is constant; therefore, there is no tangential acceleration and the direction of radial acceleration is towards the Sun. So, the instantaneous acceleration of the Earth points towards the Sun.
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
Explanation
If the speed is constant, the position vector of the particle sweeps out equal area in equal time in circular motion. Also, for constant speed, tangential acceleration is zero, i.e., constant.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
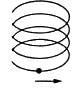
Try yourself:A particle is going in a spiral path as shown in figure with constant speed.
Explanation
As the pitch and radius of the path is constant, it shows that the magnitude of tangential and radial acceleration is also constant. Hence, the magnitude of total acceleration is constant.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
Explanation
(b) The magnitude of the frictional force on the car is greater than mv2/r
(c) The friction coefficient between the ground and the car is not less than a/g. If the magnitude of the frictional force on the car is not greater than mv2/r, it will not move forward, as its speed (v) is increasing at a rate a.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A circular road of radius r is banked for a speed v = 40 km/hr. A car of mass of m attempts to go on the circular road. The friction coefficient between the tyre and the road is negligible.
Explanation
The friction is zero and the road is banked for a speed v = 40 km/hr. If the car turns at a speed less than 40 km/hr, it will slip down.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 7- Circular Motion- 1
Try yourself:A person applies constant force 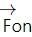 a particle of mass m and finds that the particle moves in a circle of radius r with a uniform speed v as seen from an inertial frame of reference.
a particle of mass m and finds that the particle moves in a circle of radius r with a uniform speed v as seen from an inertial frame of reference.
Explanation
We cannot move a particle in a circle by just applying a constant force. So, there are other forces on the particle.
As a constant force cannot move a particle in a circle, the resultant of other forces varies in magnitude as well as in direction (because 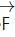 is constant).
is constant).



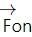 a particle of mass m and finds that the particle moves in a circle of radius r with a uniform speed v as seen from an inertial frame of reference.
a particle of mass m and finds that the particle moves in a circle of radius r with a uniform speed v as seen from an inertial frame of reference.






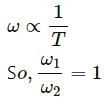
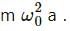
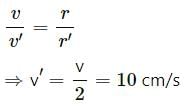
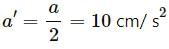
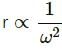
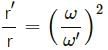
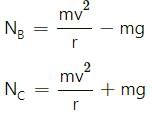

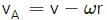
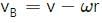
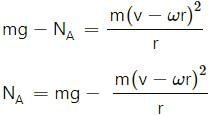
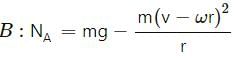

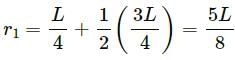
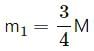
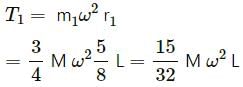
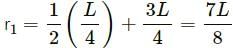
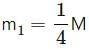

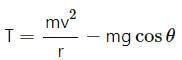
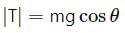
 is constant).
is constant).














