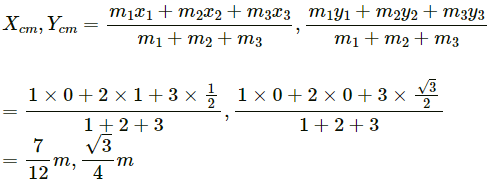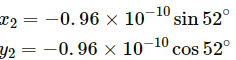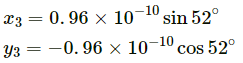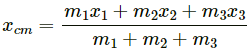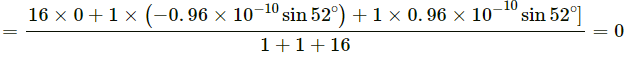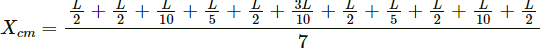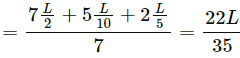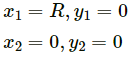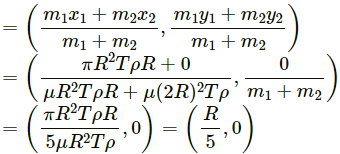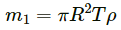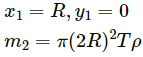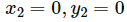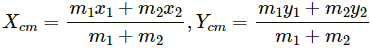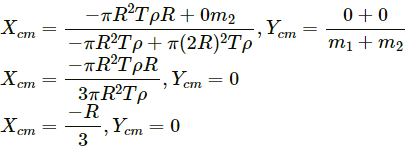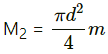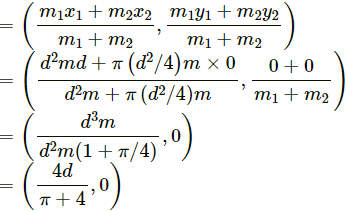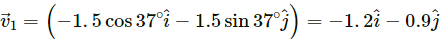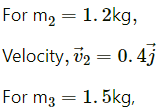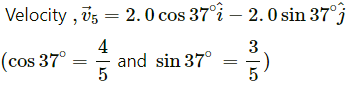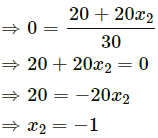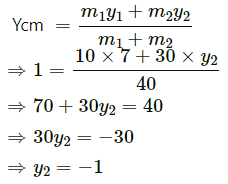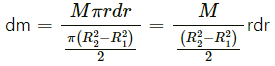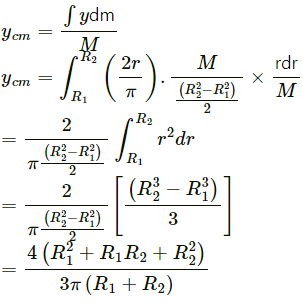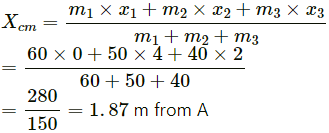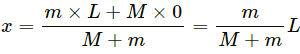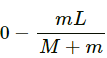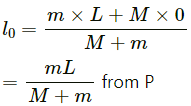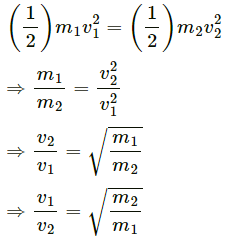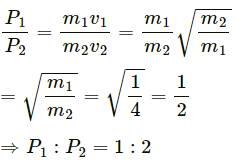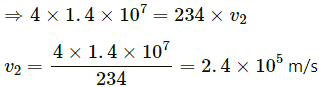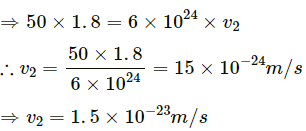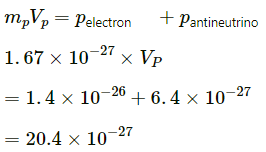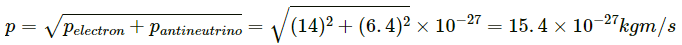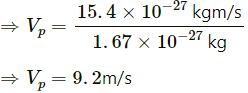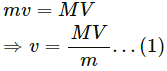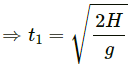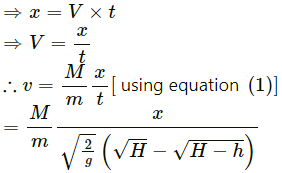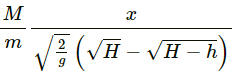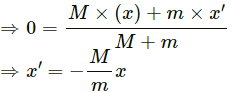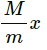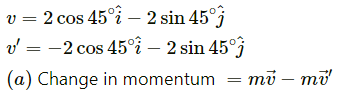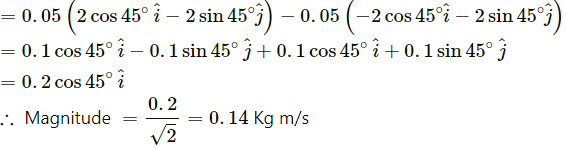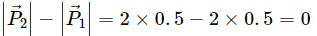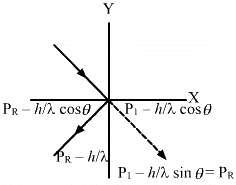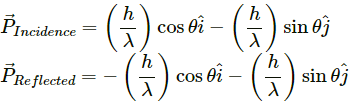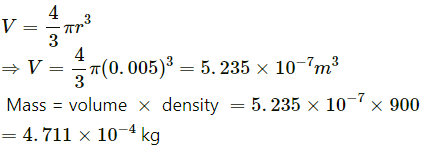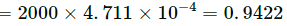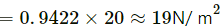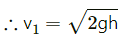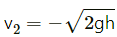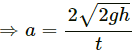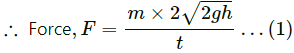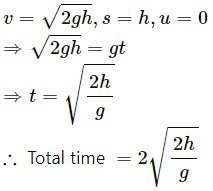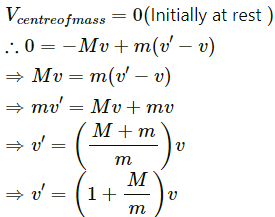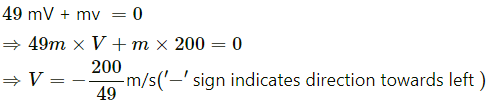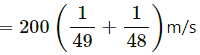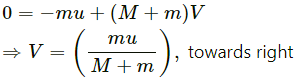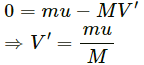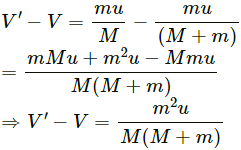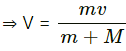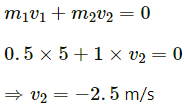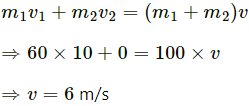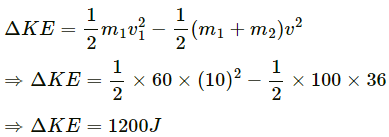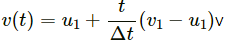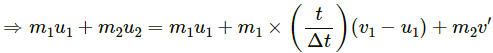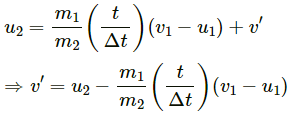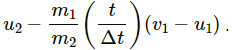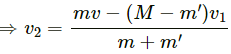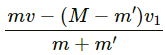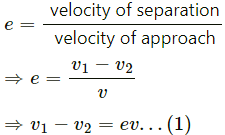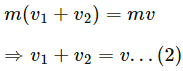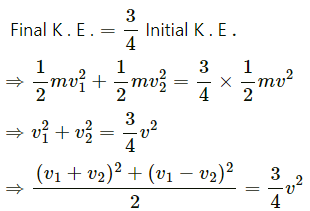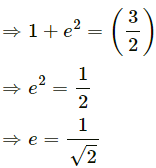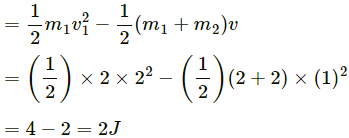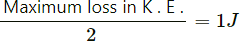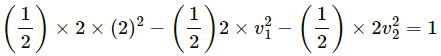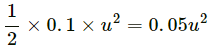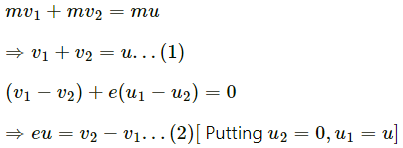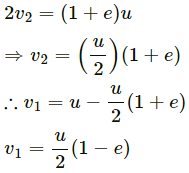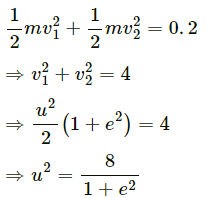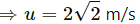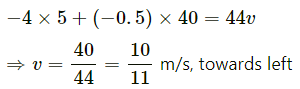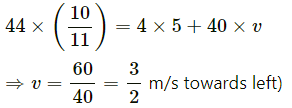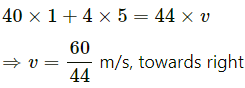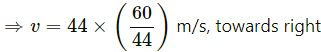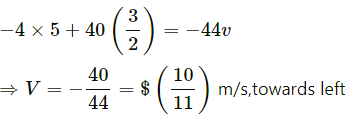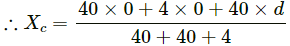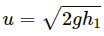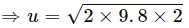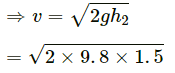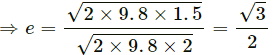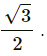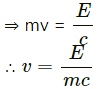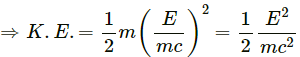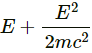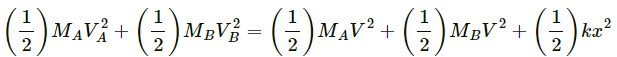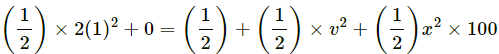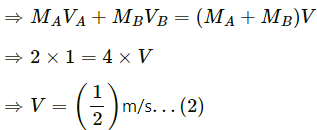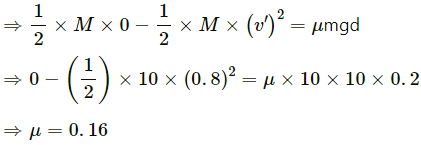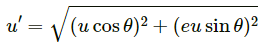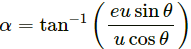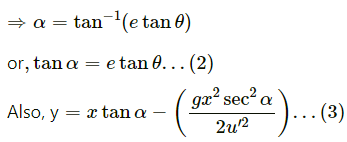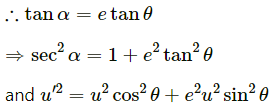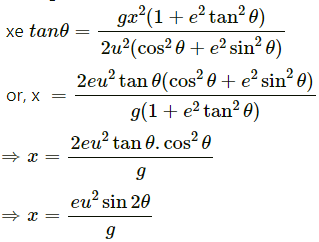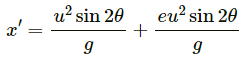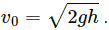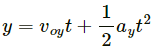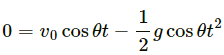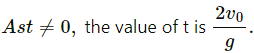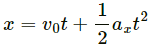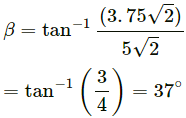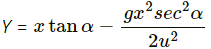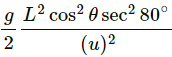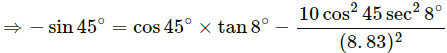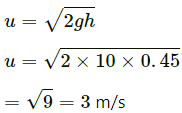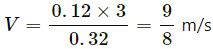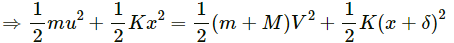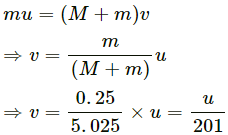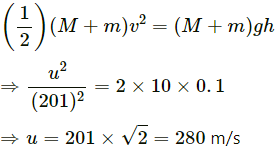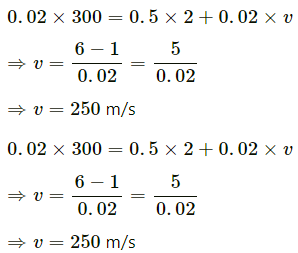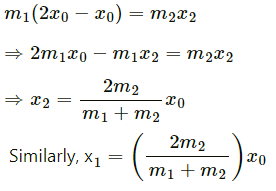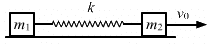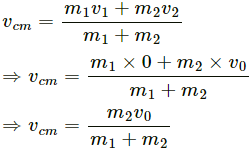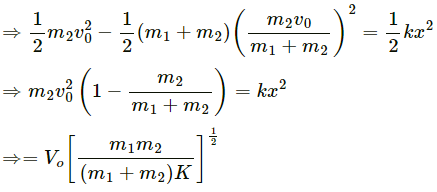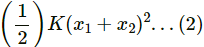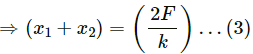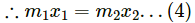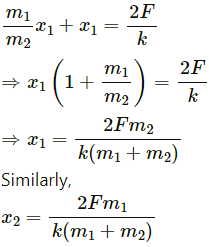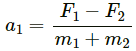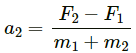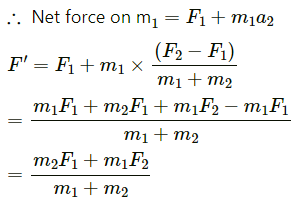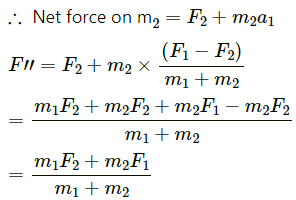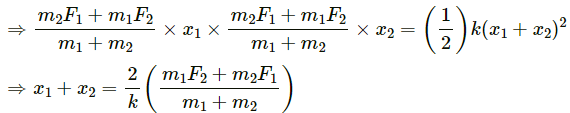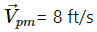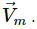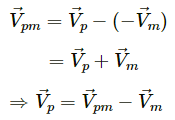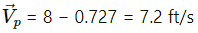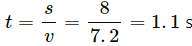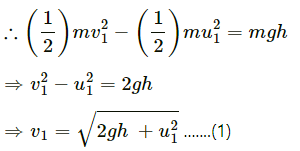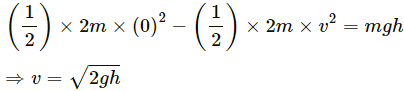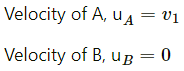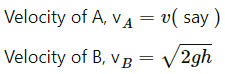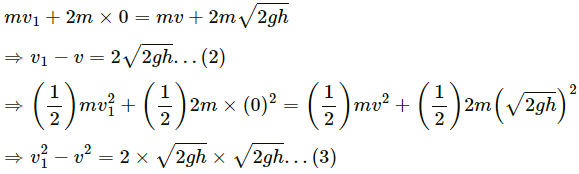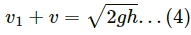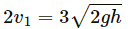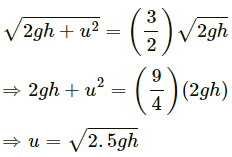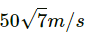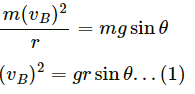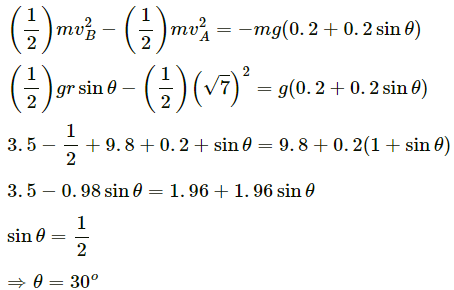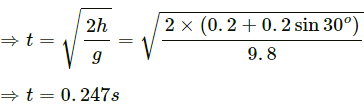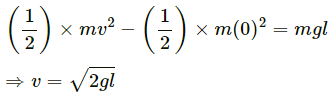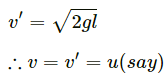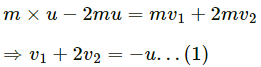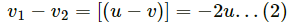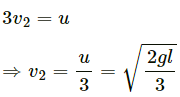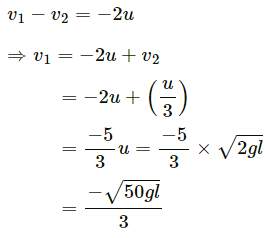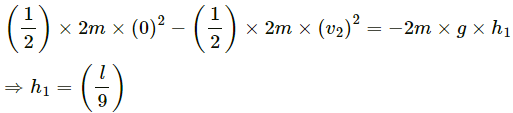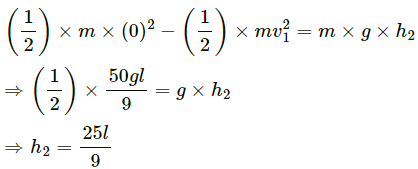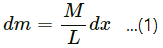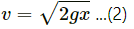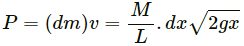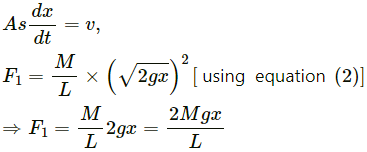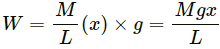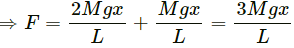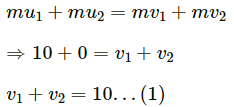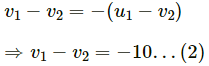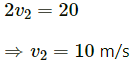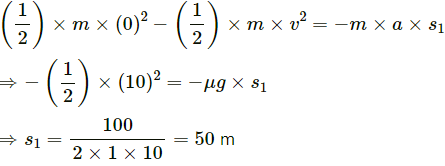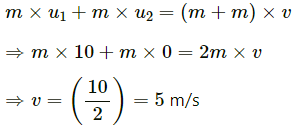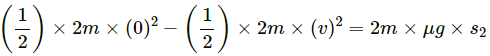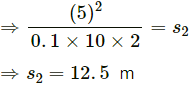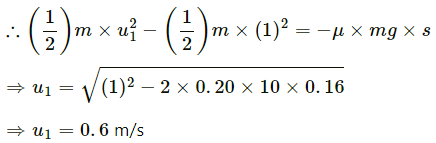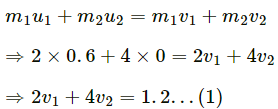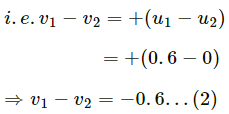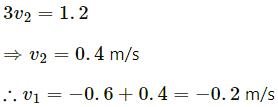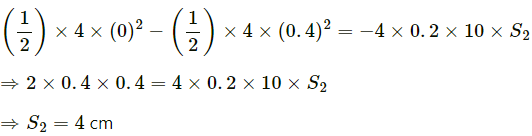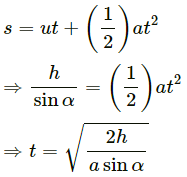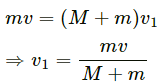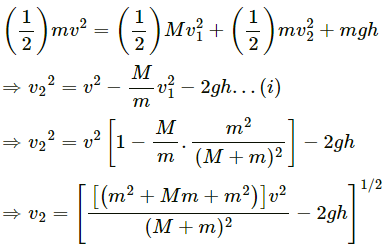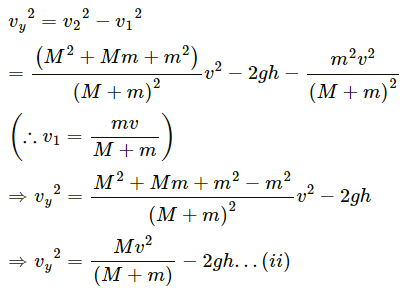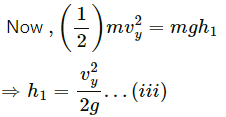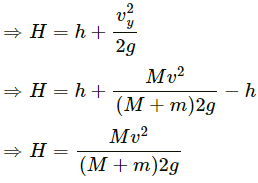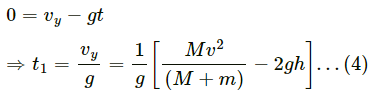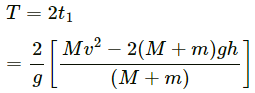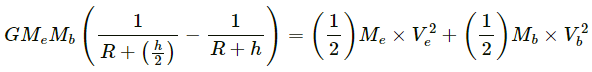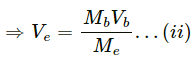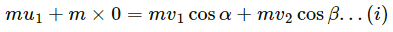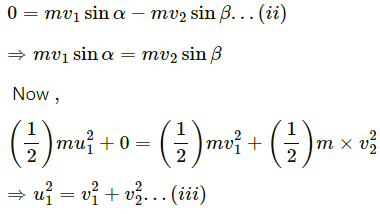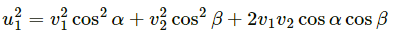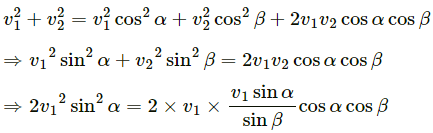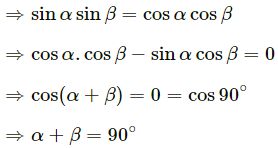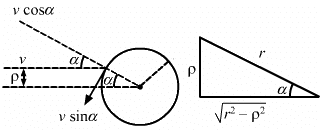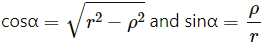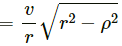HC Verma Questions and Solutions: Chapter 9: Centre of Mass, Linear Momentum, Collision- 2 | HC Verma Solutions - JEE PDF Download
Exercise
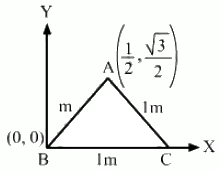
Q.1. Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
Taking BC as the X-axis and point B as the origin, the positions of masses m1 = 1 kg, m2= 2 kg and m3 = 3 kg are
respectively.
The position of centre of mass is given by:
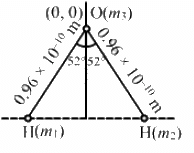
Q.2. The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.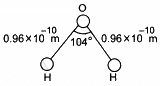
Let OX be the x-axis, OY be the Y-axis and O be the origin.
Mass of O atom, m1 = 16unit
Let the position of oxygen atom be origin.
⇒ x1 = y1 = 0
Mass of H atom ,m1 = 1unit
Now, m3 = 1unit
The X coordinate of the center of mass is given by:
The Y coordinate of the center of mass is given by:
Hence, the distance of centre of mass of the molecule from the centre of the oxygen atom is (= 6.4 x 10--12m).
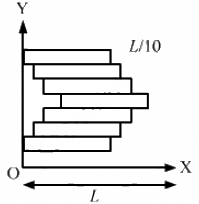
Q.3. Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate of the centre of mass relative to the origin shown.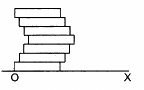
Let OX be the X-axis and point O (0, 0) be the origin of the system.
The mass of each brick is M.
The length of each brick is L.
Each brick is displaced with respect to another in contact by a distance L/10.
∴ The X-coordinate of the centre of mass is given as,
The X-coordinate of the centre of mass relative to the origin is (22L/35).
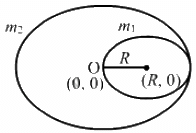
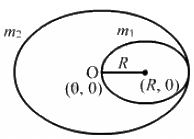
Q.4. A uniform disc of radius R is put over another uniform disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
Let the centre O (0, 0) of the bigger disc be the origin.
Radius of bigger disc = 2R
Radius of smaller disc = R
Now,
m1 = μR × T × ρ
m2 = μ (2R)2 × T × ρ
where T is the thickness of the two discs, and ρ is the density of the two discs.
Position of the centre of mass is calculated as:
⇒ The centre of mass lies at distance (R/5) from the centre of bigger disc, towards the centre of smaller disc.
Hence, the centre of mass of the system is (R/5, 0).
Q.5. A disc of radius R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
Let O be the origin of the system (smaller disc plus bigger disc).
The density of the rods is ρ.
The thickness of rods is T.
Let m1 be the mass and R be the radius of the smaller disc, and m2 be the mass and 2R be the radius of the bigger disc.
According to the question, the smaller disc is cut out from the bigger disc.
From the figure given below, we can write:
Position of centre of mass of smaller disc,
Position of centre of mass of bigger disc,
Therefore, the position of center of mass of the system,
Since the smaller disc is removed from the bigger disc, the mass of the smaller disc is taken as negative (-m1).
Hence, the centre of mass of the system lies at distance (R/3) from the centre of bigger disc, away from centre of the hole.
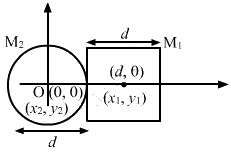
Q.6. A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.
Let m be the mass per unit area of the square plate and the circular disc .
⇒ Mass of the square plate, M1 = d2m
Mass of the circular disc,
Let the centre of the circular disc be the origin of the system.
⇒ x1 = d, y1 = 0
x2 = 0, y2 = 0
⇒ Position of the centre of mass of circular disc and square plate:
Hence, the new centre of mass of the system (circular disc plus square plate) lies at distancefrom the centre of circular disc, towards right.
Q.7. Calculate the velocity of the centre of mass of the system of particles shown in figure.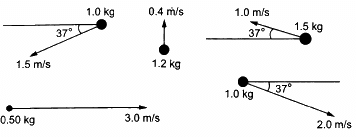
From the figure, the velocities of different masses can be written as:
For m1 = 1.0 kg,
Velocity,
On solving the above equation, we get:
Vcm is 0.20 m/s , at 45° below the direction, towards right.
Q.8. Two blocks of masses 10 kg and 20 kg are placed on the X-axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of the centre of mass unchanged?
Let the two masses m1 and m2 be placed on the X-axis.
It is given that:
m1 = 10 kg
m2 = 20 kg
The first mass is displaced by a distance of 2 cm.
As the position of the centre of mass remains unchanged,
Xcm = 0
Therefore, to keep the position of centre of mass unchanged, the block of mass 20 kg should be moved by a distance of 1 cm, towards left.
Q.9. Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
Let the two masses m1 and m2 are kept along a vertical line.
It is given that:
m1 = 10 kg
m2 = 30 kg
First block is raised through a height of 7 cm.
Thus, to raise the centre of mass by 1 cm:
Therefore, the 30 kg block (m2) should be moved by 1 cm downwards in order to raise the centre of mass by 1 cm.
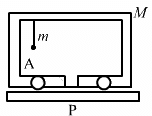
Q.10. Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend? 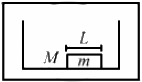
As there is no gravity or other external forces acting on the system, the melting ice tends to acquire a spherical shape. Therefore, the centre of mass of the system does not move.
Q.11. Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.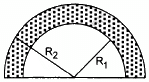
Let the mass of the plate be M.
Consider a small semicircular portion of mass dm and radius r, as shown in fig.
The centre of mass is given as:
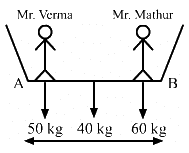
Q.12. Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
It is given that:
Mass of Mr. Verma, m1 = 50 kg
Mass of Mr. Mathur, m2 = 60 kg
Mass of boat, m3 = 40 kg
Let A be the origin of the system (boat plus two men).
Initially, Mr. Verma and Mr. Mathur were at two extremes of the boat.
∴ Distance of the centre of mass:
As no external force is experienced in longitudinal direction, the centre of mass would not shift.
Initially, the centre of mass lies at a distance of 2 m from A.
When the men move towards the middle of the boat, the centre of mass shifts and lies at 1.87 m from A.
Therefore, the shift in centre of mass = 2 − 1.87 = 0.13 m, towards right
Hence, the boat moves 13 cm or 0.13 m towards right.
Q.13. A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.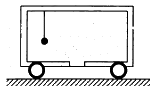
The mass of the bob is m.
The mass of the cart is M.
Considering the bob falls at point A.
Initial distance of centre of mass of the system from P is given as
When the bob falls in the slot, the distance of centre of mass of the system from P becomes zero.
∴ Shift in centre of mass =
Therefore, the cart moves a distance oftowards right.
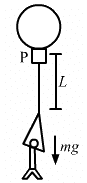
Q.14. The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.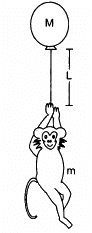
Given:
The mass of monkey is m.
The mass of balloon is M.
Initially, the monkey, balloon and the rope are at rest.
Let the centre of mass is at a point P.
When the monkey descends through a distance L,
The centre of mass shifts.
Therefore, the balloon descends through a distance
Q.15. Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
Let the masses of the two particles be m1 and m2.
Given:
m1 = 1 kg
m2 = 4 kg
Now,
Kinetic energy of the first particle = Kinetic energy of the second particle
The ratio of linear momenta (mv) of the two particles,
Therefore, the ratio of linear momenta is 1:2.
Q.16. A uranium-238 nucleus, initially at rest, emits an alpha particle with a speed of 1.4 × 107m/s. Calculate the recoil speed of the residual nucleus thorium-234. Assume that the mass of a nucleus is proportional to the mass number.
According to the question, uranium 238 nucleus emits an alpha-particle with a speed of 1.4 × 107 m/s.
Let the speed of the residual nucleus thorium 234 be v2.
By the law of conservation of linear momentum, we have:
m1v1 = m2v2
Here, m1 and v1 are the mass and velocity of the alpha-particle repectively, and m2 is the mass of the residual nucleus.
Therefore, the speed of the residual nucleus is 2.4 x 105 m/s.
Q.17. A man of mass 50 kg starts moving on the earth and acquires a speed 1.8 m/s. With what speed does the earth recoil? Mass of earth = 6 × 1024 kg.
By the law of conservation of linear momentum, we have:
m1v1 = m2v2
Here, m1 and v1 are the mass and velocity of the man respectively, and m2 and v2 are the mass and velocity of the Earth respectively.
Hence, the earth recoils with a speed of 1.5 × 10−23 m/s.
Q.18. A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
It is given that:
Mass of proton, mp = 1.67 × 10−27 kg
Momentum of electron = 1.4 × 10−26 kg m/s
Momentum of antineutrino = 6.4 × 10−27 kg m/s
Let the recoil speed of the proton be Vp.
(a) When the electron and the antineutrino are ejected in the same direction, and as the total momentum is conserved the proton should be ejected in opposite direction.
Applying the law of conservation of momentum, we get:m/s, in the opposite direction.
(b) When the electron and the antineutrino are ejected perpendicular to each other,
Total momentum of electron and antineutrino is given as,
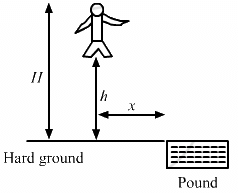
Q.19. A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?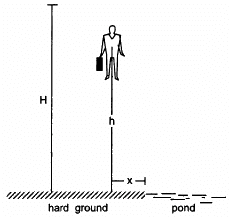
Mass of man = M
Initial velocity of the man = 0
Mass of bag = m
Let the man throws the bag towards left with a velocity v and himself moves towards right with a velocity V.
Using the law of conservation of momentum,
Let the total time he takes to reach ground be t_1 .
Let the total time he takes to reach the height h be t_2 .
∴ The time of flying in covering the remaining height h is,
During this time, the man covers a horizontal distance x and lands in the water.
Thus, the minimum horizontal velocity imparted to the bag, such that the man lands in the water is
Let the bag lands at a distance x' towards left from actual line of fall.
As there is no external force in horizontal direction, the x-coordinate of the centre of mass will remain same.
Therefore, the bag will land at a distance
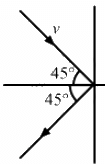
Q.20. A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
It is given that:
Mass of the ball = 50 g = 0.05kg
Speed of the ball, v = 2.0 m/s
Incident angle = 45˚
(b) The change in magnitude of the momentum of the ball,
i.e. There is no change in magnitude of the momentum of the ball.
Q.21. Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
It is given that:
Wavelength of light = λ
Momentum of each photon = h/λ
Angle of incidence = θ
The change in momentum will only be in the direction of x - axis i . e . ,
Q.22. A block at rest explodes into three equal parts. Two parts start moving along X and Y axes respectively with equal speeds of 10 m/s. Find the initial velocity of the third part.
As the block is exploded only because of its internal energy, the net external force on the system is zero.
Thus, the centre of mass of does not change.
Let the body was at the origin of the co-ordinate system during explosion.
Resultant velocity of two bodies of equal mass moving at a speed of 10 m/s in + x-axis and + y-axis direction, is given as:
If the centre of mass is at rest, the third part having equal mass as that of the other two masses will move in the opposite direction (i.e. 135º w.r.t. +x-axis) at the same velocity of 10√2 m/s.
Q.23. Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
According to the question, the spaceship is removed from all other material objects and kept totally isolated from the surroundings. Thus, the mass loss by astronauts couldn't slip away from the spaceship. Therefore, the total mass of the spaceship remains unchanged and so does its velocity.
Hence, the spaceship moves with the speed of 15 km/s.
Q.24. During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
It is given that:
Diameter of hailstone = 1 cm = 0.01 m
⇒ Radius of hailstone, r = 0.005 m
Average speed of hailstone = 20 m/s
Density of hailstone = 900 kg/m3 = 0.9 g/cm3
Volume of the hailstones is given as,
∴ Mass of 2000 hailstone
Rate of change of momentum
∴ The total force exerted on the roof = 19 × 100 = 1900 N
Q.25. A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
It is given that the mass of the ball is m.
Let the ball be dropped from a height h.
The speed of ball before the collision is v1.
The speed of ball after the collision is v2.
Rate of change of velocity = acceleration
Using Newton's laws of motion, we can write:
Substituting this value of time t in equation (1), we get:
F = mg
Q.26. A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
Given:
The mass of the railroad car is M.
The mass of the man is m.
The car recoils with a speed v, backwards on the rails.
Let the man of mass m approaches towards the engine with a velocity v' w.r.t the engine.
∴ The velocity of man w.r.t earth is v' − v, towards right.
Q.27. A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
It is given that:
Mass of the car, the gun, the shells and the operator = 50m
Mass of one shell = m
Muzzle velocity of the shells, v = 200 m/s
Let the speed of car be v.
On applying the law of conservation of linear momentum, we get:
Thus, when another shell is fired, the velocity of the car with respect to the platform is, V = (200/49) m/s, towards left
When one more shell is fired, the velocity of the car with respect to the platform is, V1 = (200/48) m/s, towards left
When one more shell is fired, the velocity of the car with respect to the platform is, V1 = 200/48) m/s, towards left
∴ Velocity of the car w.r.t the earth
Q.28. Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.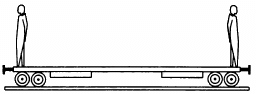
It is given that:
Mass of each persons = m
Mass of railroad car = M
Let the velocity of the railroad w.r.t. earth, when the man on the left jumps off be V.
By the law of conservation of momentum:
When the man on the right jumps, his velocity w.r.t. the car is u.
(V is the change in velocity of the platform when the platform itself is taken as reference, assuming the car to be at rest.)
∴ Net velocity towards left, (i.e. the velocity of the car)
Q.29. Figure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mass M placed on a horizontal floor. The curved part of the surface shown in semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.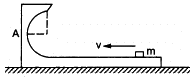
The mass of the small block is m.
Initial speed of this block is v.
The mass of the bigger block is M.
Initial speed of this block is zero.
At point A, as the small block transfers its momentum to the bigger block, both the blocks move with a common velocity V (say) in the same direction as v.
Using the law of conservation of linear momentum, we can write:
Initial momentum = final momentum
MV + M × O = ( m +M)V
Therefore, the speed of the bigger block when the smaller block reaches point A of the surface is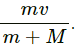
Q.30. In a typical Indian Bugghi (a luxury cart drawn by horses), a wooden plate is fixed on the rear on which one person can sit. A bugghi of mass 200 kg is moving at a speed of 10 km/h. As it overtakes a school boy walking at a speed of 4 km/h, the boy sits on the wooden plate. If the mass of the boy is 25 kg, what will be the plate. If the mass of the boy is 25 kg, what will be the new velocity of the bugghi ?
It is given that:
Mass of the bugghi, mb = 200 kg
Velocity of the bugghi, Vb = 10 km/h
Mass of the boy, mboy = 25 kg
Velocity of the boy, VBoy = 4 km/h
Consider the boy and the bugghi as a system.
The total momentum before the process of sitting remains same after the process of sitting.
Using the law of conservation of momentum, we can write: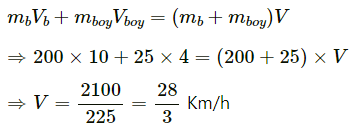
Q.31. A ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mass 1.0 kg. After the collision the balls stick together and remain motionless. What was the velocity of the 1.0 kg block before the collision?
It is given that:
Speed of the ball, v1 = 5.0 m/s
Mass of the ball, m1 = 0.5 kg
Mass of another ball, m2 = 1 kg
Let the velocity of this ball be v2 m/s.
On applying the law of conservation of momentum, we get:
Hence, the velocity of second ball is 2.5 m/s, opposite to the direction of motion of the first ball.
Q.32. A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
It is given that:
Mass of the skater who is skating, m1 = 60 kg
Initial speed of this man, v1 = 10 m/s
Mass of the skater at rest, m2 = 40 kg
Initial speedof this man, v2 = 0
Let the velocity of both men after collision be v.
Using the law of conservation of momentum, we can write:
The loss in kinetic energy during collision is given as,
Q.33. Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as 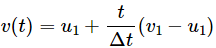
Find the speed of the second particle as a function of time during the collision.
It is given that:
Speed of the first particle during collision,
Let v' be the speed of the second particle, during collision.
On applying the law of conservation of linear momentum on both particles, we get:
m1u1 + m2u2 = m1v(t) + m2v'
On dividing both the sides by m2, we get:
The speed of the second particle during collision can be written as a function of time and is given by the expression,
Q.34. A bullet of mass m moving at a speed v hits a ball of mass M kept at rest. A small part having mass m breaks from the ball and sticks to the bullet. The remaining ball is found to move at a speed v1 in the direction of the bullet. Find the velocity of the bullet after the collision.
Given:
The mass of bullet moving with speed v is m.
The mass of the ball is M and it is at rest.
m' is the fractional mass of the ball that sticks with the bullet.
The remaining mass of the ball moves with the velocity v1.
Let v2 be the final velocity of the bullet plus fractional mass system.
On applying the law of conservation of momentum, we get:
mv + 0 = (m' + m)v2 + (M − m') v1
Therefore, the velocity of the bullet after the collision is
Q.35. A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
Given:
The mass of the both balls is m.
Initial speed of first ball = v
Initial speed of second ball = 0
Let the final of balls be v1 and v2 respectively.
On applying the law of conservation of linear momentum, we get:
According to the given condition,
Hence, the coefficient of restitution is found to be.
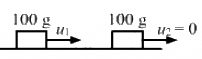
Q.36. A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
It is given that:
Mass of first block, m1 = 2 kg
Initial speed, v1 = 2.0 m/s
Mass of second block, m2 = 2 kg
Initial speed of this block = 0
For maximum possible loss in kinetic energy, we assume that the collision is elastic and both the blocks move with same final velocity v (say).
On applying the law of conservation of linear momentum, we get:
m1v1 + m2 ×0 = (m1+m2)v
2 × 2 = (2 + 2)v
⇒ v = 1 m/s
Loss in K.E. in elastic collision is give by,
(b) The actual loss in K . E . =
Let the final velocities of the blocks be v1 and v2 respectively. The coefficient of restitution is e.
∴ The loss in K.E. is given by,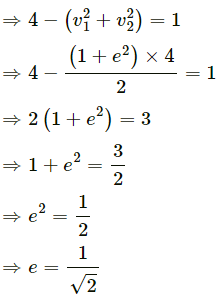
Q.37. A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
It is given that:
Mass of particles = 100 g
Initial speed of the first particle = u
Final K.E. of the system after collision = 0.2J
Initial K.E. of the system, before collision =
i.e. Initial K.E. =
Let v1 and v2 be the final velocities of the first and second block respectively.
Let v1 and v2 be the final velocities of the first and second block respectively.
By law of conservation of momentum, we know:
Adding the equations (1) and (2), we get:
According to given condition,
For maximum value of u, denominator should be minimum in the above equation.
i.e. e = 0
⇒ u2 = 8
For minimum value of u, denominator should have maximum value.
i.e. e = 1
⇒ u2 = 4
⇒ u = 2 m/s .
Q.38. Two friends A and B (each weighing 40 kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4 kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5 m/s on the platform. (a) Find the speed of A after he catches the ball for the first time. (c) Find the speeds of A and B after the all has made 5 round trips and is held by A. (d) How many times can A roll the ball? (e) Where is the centre of mass of the system "A + B + ball" at the end of the nth trip?
It is given that:
Weight of A = Weight of B = 40 kg
Velocity of ball = 5 m/s
(a) Case-1: Total momentum of the man A and ball remains constant.
∴ 0 = 4 × 5 − 40 × v
⇒ v = 0.5 m/s, towards left
(b) Case-2: When B catches the ball, the momentum between B and the ball remains constant.
⇒ 4 × 5 = 44 v
Case-3: When B throws the ball,
On applying the law of conservation of linear momentum, we get:
⇒ v = 1 m/s , towards right)
Case-4: When A catches the ball,
Applying the law of conservation of liner momentum, we get:
(c) Case-5: When A throws the ball,
Applying the law of conservation of linear momentum, we get:
Case-6: When B receives the ball,
Applying the law of conservation of linear momentum, we get:
Case-7: When B throws the ball,
On applying the law of conservation of linear momentum, we get:
Case-8: When A catches the ball,
On applying the law of conservation of linear momentum, we get:
Similarly, after 5 round trips,
The velocity of A will be (50/11) m/s and the velocity of B will be 5 m/s.
(d) As after 6 round trips, the velocity of A becomes (60/11)>5 m/s, it cannot catch the ball. Thus, A can only roll the ball six times.
(e) Let the ball and the body A be at origin, in the initial position.
= (10/21)d
Q.39. A ball falls on the ground from a height of 2.0 m and rebounds up to a height of 1.5 m. Find the coefficient of restitution.
Let the velocity of the ball falling from height h1 be u (when it approaches the ground).
Velocity on the ground,
Let the velocity of ball when it separates from the ground be v. (Assuming it goes up to height h2)
Let the coefficient of restitution be e.
We know, v = eu
Hence, the coefficient of restitution is
Q.40. In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
Let the nucleus recoils with a velocity v.
Applying the law of conservation of linear momentum, we get:
Linear momentum of recoiled nucleus = Linear momentum of gamma photon
Kinetic energy of the recoiled nucleus =
Decrease in the internal energy = photon energy + the kinetic energy of the recoiled nucleus
⇒ Decrease in the internal energy =
Q.41. A block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s (In the following figure) towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.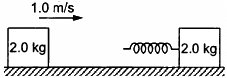
Given,
Mass of each block, MA = MB = 2 kg
Initial velocities of block A, Va = 1 m/s
Initial velocity of block B, Vb = 0
Spring constant of the spring = 100 N/m
Block A strikes the spring with a velocity of 1 m/s.
After the collision, it's velocity decreases continuously. At an instant the whole system (Block A + the compound spring + Block B) moves together with a common velocity V (say).
Using the law of conservation of energy, we get:
(where x is the maximum compression of the spring)
⇒ 1 − 2v2 = 50x2 ...(1)
As there is no external force acting in the horizontal direction, the momentum is conserved.
Susbstituting this value of V in equation (1), we get:
Q.42. A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
It is given that:
Mass of bullet, m = 20 g =0.02 kg
The initial speed, v1 = 500 m/s
Mass of block, M = 10 kg
The initial speed of block = 0
Final velocity of bullet, v2= 100 m/s
Let the final velocity of block when the bullet emerges out = v'
Applying conservation of linear momentum,
mv1 + M × 0 = mv2 + Mv'
⇒ 0.02 × 500 = 0.02 × 100 + 10 × v'
⇒ v' = 0.8 m/s
Distance covered by the block, d = 20 cm = 0.02 m .
Let friction coefficient between the block and the surface = μ
Thus, the value of friction force, F = μmg
Change in K.E. of block = Work done by the friction force
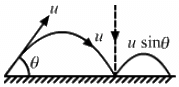
Q.43. A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
Given:
Initial velocity of the projectile = u
Angle of projection of the projectile with respect to ground = θ
When the projectile hits the ground for the first time, the velocity remains same i.e. u.
The component of velocity parallel to ground, u cos θ should remain constant.
However, the vertical component of the projectile undergoes a change after the collision.
If the coefficient of restitution of collision between the projectile and the field is e,
The velocity of separation is given by,
⇒ v = eu sin θ
Therefore, for the second projectile motion,
Velocity of projection (u') will be,
Angle of projection,
Here, y = 0
Putting the above calculated values in equation (3), we get:
Thus, from the starting point the projectile makes its second collision with the field at a distance,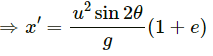
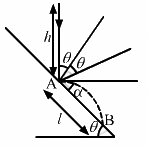
Q.44. A ball falls on an inclined plane of inclination θ from a height h above the point of impact and makes a perfectly elastic collision. Where will it hit the plane again?
Given:
The angle of inclination of the inclined plane is θ.
A ball falls on the inclined plane from height h.
The coefficient of restitution is e.
Let the ball strikes the inclined plane at origin with velocity
As the ball elastically rebounds, it recalls with the same velocity v0 at the same angle θ from the normal or y-axis.
Let the ball strikes the incline second time at any point P, which is at a distance l from the origin along the incline.
From the equation,
we may write:
where t is time of motion of the ball in air, as the ball moves from origin to point P.
Now from the equation,
we can write,
Substituting the value of v0 in the above equation, we get:
l = 8h sin θ
Therefore, the ball again hits the plain at a distance, l = 8h sin θ.
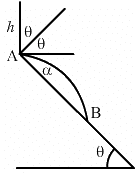
Q.45. Solve the previous problem if the coefficient of restitution is e. Use θ = 45° e = 3/4 and h = 5 m.
Given:
The angle of inclination of the plane, θ = 45°
A ball falls on the inclined plane from a height (h) of 5 m.
The coefficient of restitution, e = (3/4)
The velocity with which ball strikes the inclined plane is given as,
The ball makes an angle β with the horizontal, after the collision.
The horizontal component of velocity, 10cos45° remains unchanged.
However, the velocity in perpendicular direction to the plane after the collision will now be:
Now,
Angle of reflection from the wall is given as,
Angle of projection α = 90 − (θ + β)
⇒ α = 90° − (45° + 37°) = 8°
Let the distance where the ball falls after the collision be L.
⇒ x = L cos θ
Angle of projection (α) = −8°
Now,
⇒ −L sin θ = L cos θ × tan 8° -
On solving the above equation, we get:
L = 18.5 m
Q.46. A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
It is given that:
Mass of block, M = 200 g = 0.20 kg
Mass of the particle, m = 120 gm = 0.12 kg
Height of the particle, h = 45 cm = 0.45 m
According to question, as the block attains equilibrium, the spring is stretched by a distance, x = 1.00 cm = 0.01 m.
i.e. M × g = K × x
⇒ 0.2 × g = K × x
⇒ 2 = K × 0.01
⇒ K = 200 N/m
The velocity with which the particle m strikes M is given by,
After the collision, let the velocity of the particle and the block be V.
According to law of conservation of momentum, we can write:
mu = (m + M)V
Solving for V , we get:
Let the spring be stretched through an extra deflection of δ.
On applying the law of conservation of energy, we can write:
Initial energy of the system before collision = Final energy of the system
Substituting appropriate values in the above equation, we get:
On solving the above equation, we get:
δ = 0.061
m = 6.1 cm
Q.47. A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.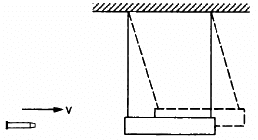
Given:
Mass of bullet, m = 25 g = 0.025 kg
Mass of ballistic pendulum, M = 5 kg
Vertical displacement, h = 10 cm = 0.1 m
Let the bullet strikes the pendulum with a velocity u.
Let the final velocity be v.
Using the law of conservation of linear momentum, we can write:
Applying the law of conservation of energy, we get:
The bullet strikes the pendulum with a velocity of 280 m/s.
Q.48. A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
Given:
Mass of bullet, m = 20 gm = 0.02 kg
Horizontal speed of the bullet, u = 300 m/s
Mass of wooden block, M = 500 gm = 0.5 kg
Let the bullet emerges out with velocity v.
Let the velocity of the block be v'.
Using the law of conservation of momentum, we get:
mu = Mv' + mv ...(1)
Now, applying the work-energy principle for the block after the collision, we get:
On substituting the value of v' in equation (1), we get:
Hence, the speed of the bullet as it emerges out from the block is 250 m/s.
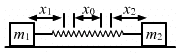
Q.49. Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
It is given that two blocks of masses m1 and m2 are connected with a spring having spring constant k.
Initially the spring is stretched by a distance x0.
For the block to come to rest again,
Let the distance travelled by m1 be x1 (towards right), and that travelled by m2 be x2 towards left.
As no external force acts in horizontal direction, we can write:
m1x1 = m2x2 ...(1)
As the energy is conserved in the spring, we get:
Putting this value in equation (1), we get:
Q.50. Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.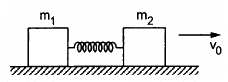
Given,
Velocity of mass, m2 = v0
Velocity of mass, m1 = 0
(a) Velocity of centre of mass is given by,
(b) Let the maximum elongation in spring be x.
The spring attains maximum elongation when velocities of both the blocks become equal to the velocity of centre of mass.
i.e. v1 = v2 = vcm
On applying the law of conservation of energy, we can write:
Change in kinetic energy = Potential energy stored in spring
Q.51. Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
It is given that the force on both the blocks is F.
Let x1 and x2 be the extensions of blocks m1 and m2 respectively.
Total work done by the forces on the blocks = Fx1 + Fx2 ...(1)
∴ Increase in the potential energy of spring =
Equating the equations (1) and (2), we get:
As the net external force on the system is zero, the centre of mass does not shift.
Using the equations (3) and (4), we get:
Q.52. Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
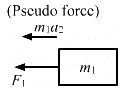
Given:
Force on block of mass, m1 = F1
Force on block of mass, m2 = F2
Let the acceleration produced in mass m1 be a1.
Let the acceleration of mass m2 be a2.
Due to the force F2, the mass m1 experiences a pseudo force.
Similarly, mass m2 experiences a pseudo force due to force F1.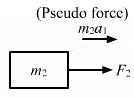
Let m1 be displaced by a distance x1 and m2 be displaced by a distance x2.
Therefore, the maximum elongation of the spring = x1 + x2
Work done by the blocks = Energy stored in the spring
Q.53. Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
Given,
Mass of the man, Mm = 50 kg
Mass of the pillow, MP = 5 kg
Velocity of pillow w.r.t. man,
Let the velocity of man be
As no external force acts on the system, the acceleration of centre of mass is zero and the velocity of centre of mass remains constant.
Using the law of conservation of linear momentum:
Mm × Vm = Mp × Vp ...(1)
∴ Velocity of pillow,
The time taken to reach the floor is given by,
As the mass of wall is much greater than the mass of the pillow, velocity of block before the collision = velocity after the collision
⇒ time of ascent = 1.11 s
Hence, total time taken = 1.11 + 1.11 = 2.22 s
Q.54. The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between A and B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened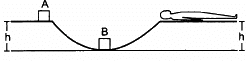
Given:
Mass of the block, A = m
Mass of the block, B = 2m
Let the initial velocity of block A be u1 and the final velocity of block A,when it reaches the block B be v1.
Using the work-energy theorem for block A, we can write:
Gain in kinetic energy = Loss in potential energy
Let the block B just manages to reach the man's head.
i.e. the velocity of block B is zero at that point.
Again, applying the work-energy theorem for block B, we get:
Therefore, before the collision:
After the collision:
As the collision is elastic, K.E. and momentum are conserved.
Dividing equation (3) by equation (2), we get:
Adding the equations (4) and (2), we get:
Now using equation (1) to substitue the value of v1, we get:
Block a should be started with a minimum velocity ofto get the sleeping man awakened.
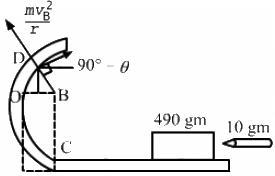
Q.55. A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?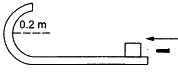
Given:
Mass of block = 490 gm
Initial speed of the block = 0
Mass of bullet = 10 gm
Initial speed of the bullet, v1 =
As the bullet gets embedded inside the block, this is an example of a perfectly inelastic collision.
Let the final velocity of the system (block and bullet) be VA.
Using the law of conservation of linear momentum, we get:
m1 + m2 × 0 = ( m1 + m2 ) VA
⇒ 10 × 10 - 3 × 507 + 490 × 10 - 3 × 0 = (490 + 10) × 10 - 3 × vA
When the block loses contact at D, the component mg acts on it. Let the velocity at D be vB.
Using work energy theorem
∴ Angle of projection = 90° − 30° = 60°
Time of reaching the ground,
Distance travelled in the horizontal direction is given by,
S = v cos θ × t
S = gr sin θ cos θ×t
S = 9.8 × 2 × 1232 × 0.247
S = 0.196 m
Total distance = (0.2 − 0.2 cos 30° + 0.196)
= 0.22 m
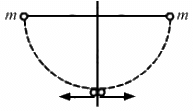
Q.56. Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?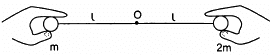
Given:
Mass of the 1st ball = m
Mass of the 2nd ball = 2m
When the balls reach the lower end,
Let the velocity of m be v; and the velocity of 2m be v'.
Using the work-energy theorem, we can write:
Similarly, velocity of block having mass 2m will be,
Let the velocities of m and 2m after the collision be v1 and v2 respectively.
Using the law of conservation of momentum, we can write:
On applying collision formula, we get:
Substracting equation (1) from (2), we get:
Substituting this value in equation (1), we get:
(b) Let the heights reached by balls 2m and m be h1 and h respectively.
Using the work energy principle, we get:
Similarly,
As h2 is more than 2l, the velocity at the highest point will not be zero.
Also, the mass m will rise by a distance 2l.
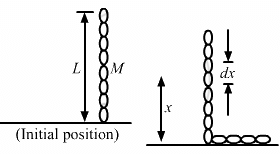
Q.57. A uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to test. Assuming that the chain does not form a heap on the floor calculate the force exerted by it on the floor when a length x has reached the floor.
Given is a uniform chain of mass M and length L.
Let us consider a small element of chain at a distance x from the floor having length 'dx'.
Therefore, mass of element,
The velocity with which the element strikes the floor is,
∴ The momentum transferred to the floor is,
According to the given condition, the element comes to rest.
Thus, the force (say F1) exerted on the floor = Change in momentum(for the chain element)
Again, the force exerted due to length x of the chain on the floor due to its own weight is given by,
Thus, the total force exerted is given by.
F = F1 + W
where W is the weight of chain below the element dx up to the floor.
Q.58. The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
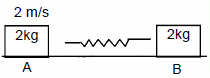
Given,
Speed of the block A = 10 m/s
The block B is kept at rest.
Coefficient of friction between floor and block B, μ = 0.10
Lets v1 and v2 be the velocities of A and B after collision respectively.
(a) If the collision is perfectly elastic, linear momentum is conserved.
Using the law of conservation of linear momentum, we can write:
We know,
Velocity of separation (after collision)= Velocity of approach (before collision)
Substracting equation (2) from (1), we get:
The deceleration of block B is calculated as follows:
Applying the work energy principle, we get:
(b) If the collision is perfectly inelastic, we can write:
The two blocks move together, sticking to each other.
∴ Applying the work-energy principle again, we get:
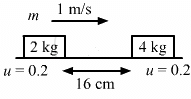
Q.59. The friction coefficient between the horizontal surface and each of the block shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g = 10 m/s2.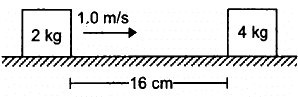
Given:
Initial velocity of 2 kg block, v1 = 1.0 m/s
Initial velocity of the 4 kg block, v2 = 0
Let the velocity of 2 kg block, just before the collision be u1.
Using the work-energy theorem on the block of 2 kg mass:
The separation between two blocks, s = 16 cm = 0.16 m
As the collision is perfectly elastic, linear momentum is conserved.
Let v1, v2 be the velocities of 2 kg and 4 kg blocks, just after collision.
Using the law of conservation of linear momentum, we can write:
For elastic collision,
Velocity of separation (after collision) = Velocity of approach (before collision)
Substracting equation (2) from (1), we get:
Let the 2 kg block covers a distance of S1.
∴ Applying work-energy theorem for this block, when it comes to rest:
Let the 4 kg block covers a distance of S2.
Applying work energy principle for this block:
Therefore, the distance between the 2 kg and 4 kg block is given as,
S1 + S2 = 1 + 4 = 5 cm
Q.60. A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.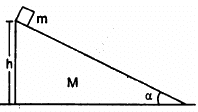
According to the question, the surface is frictionless. Thus, the block m will slide down the inclined plane of mass M.
Acceleration, a1 = g sin α (Relative to the inclined plane)
The horizontal component of acceleration a1 is given by ax = g sin α cos α, for which the block M accelerates towards left.
Let the left acceleration be a2.
By the concept of centre of mass, we can say that the external force is zero in the horizontal direction.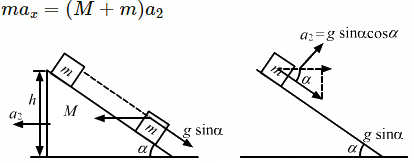
Absolute (resultant) acceleration of m on the plane M, along the direction of the incline will be = a = g sinα - α2 cos α
Let the time taken by the block m to reach the bottom end be t.
Now,
Thus, the velocity of the bigger block after time t will be,
Q.61. Figure shows a small body of mass m placed over a larger mass M whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed v and the system is left to itself. Assume that all the surface are frictionless. (a) Find the speed of the larger block when the smaller block is sliding on the vertical part. (b) Find the speed of the smaller mass when it breaks off the larger mass at height h. (c) Find the maximum height (from the ground) that the smaller mass ascends. (d) Show that the smaller mass will again land on the bigger one. Find the distance traversed by the bigger block during the time when the smaller block was in its flight under gravity.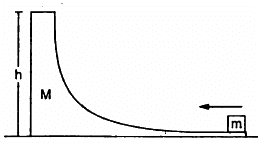
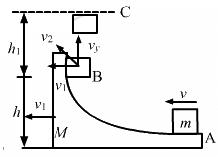
According to the question, mass m is given with a speed v over the larger mass M.
(a) When the smaller block travels on the vertical part, let the velocity of the bigger block be v1, towards left.
From the law of conservation of momentum (in the horizontal direction), we get:
(b) When the smaller block breaks off, let its resultant velocity be v2.
Using the law a of conservation of energy, we get:
(c) Vertical component of the velocity v2 of mass m is given by,
To determine the maximum height (from the ground),
Let us assume that the body rises to a height h1 over and above h.
∴ Total height, H = h + h1
(d) Because the smaller mass also has a horizontal component of velocity V1 at the time it breaks off from M (that has a velocity v1), the block m will again land on the block M.
The time of flight of block m after it breaks off is calculated as:
During the upward motion (BC),
Thus, the time for which the smaller block is in flight is given by,
The distance travelled by the bigger block during this time is, S = v1T
Q.62. A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
It is given that h is much lesser than the radius of the earth.
Mass of the earth, Me = 6 × 1024 kg
Mass of the block, Mb = 3 × 1024 kg
Let Ve be the velocity of earth and Vb be the velocity of the block.
Let the earth and the block be attracted by gravitational force.
Thus, according to the conservation law of energy, the change in the gravitational potential energy will be the K.E. of block.
As only the internal force acts in this system, the momentum is conserved.
MeVe = MbVb
Q.63. A body of mass m makes an elastic collision with another identical body at rest. Show that if the collision is not head-on the bodies go at right angle to each other after the collision.
According to the question, the collision of the two bodies of mass m is not head-on. Thus, the two bodies move in different directions.
Let the velocity vectors of the two bodies after collision be v1 and v2.
As the collision in the question is elastic, momentum is conserved.
On applying the law of conservation of momentum in X-direction, we get:
On applying the law of conservation of momentum in Y-direction, we get:
On squaring equation (i), we get:
Equating the equations (i) and (iii), we get
Q.64. A small particle travelling with a velocity v collides elastically with a spherical body of equal mass and of radius r initially kept at rest. The centre of this spherical body is located a distance ρ(< r) away from the direction of motion of the particle (see figure below). Find the final velocities of the two particles.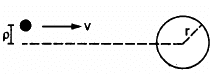
[Hint : The force acts along the normal to the sphere through the contact. Treat the collision as one dimensional for this direction. In the tangential direction no force acts and the velocities do not change].
It is given that the mass of both the bodies (small particle and spherical body) is same.
Let the velocity of the particle be v.
We break the particle velocity into two components: v cosα (normal to the sphere) and v sinα (tangential to the sphere).
From figure,
Here, the collision occurs due to the component v cosα.
After an elastic collision, bodies of same mass exchange their respective velocities.
Thus, the spherical body will have a velocity v cosα, while the particle will not have any component of velocity in this direction.
However, the tangential velocity of the particle v sinα will remain unaffected.
Thus, we have:
Velocity of the sphere = v cosα
And,
Velocity of the particle = v sinα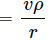
|
134 docs
|