Class 7 Maths Chapter 6 HOTS Questions - The Triangle and Its Properties
Q1: In the following figure, find the unknown angles a and b, if l || m.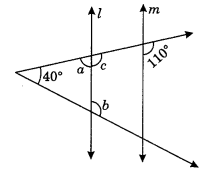
Sol:
Here, l || m
∠c = 110° (Corresponding angles)
∠c + ∠a = 180° (Linear pair)
⇒ 110° + ∠a = 180°
⇒ ∠a = 180° – 110° = 70°
Now ∠b = 40° + ∠a (Exterior angle of a triangle)
⇒ ∠b = 40° + 70° = 110°
Hence, the values of unknown angles are a = 70° and b = 110°
Q2: In figure (i) and (ii), Find the values of a, b and c.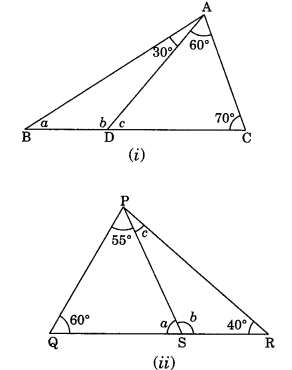
Sol:
(i) In ∆ADC, we have
∠c + 60° + 70° = 180° (Angle sum property)
⇒ ∠c + 130° = 180°
⇒ ∠c = 180° – 130° = 50°
∠c + ∠b = 180° (Linear pair)
⇒ 50° + ∠b = 180°
⇒ ∠ b = 180° – 50° = 130°
In ∆ABD, we have
∠a + ∠b + 30° = 180° (Angle sum property)
⇒ ∠a + ∠130° + 30° = 180°
⇒ ∠a + 160° = 180°
⇒ ∠a = 180° – 160° = 20°
Hence, the required values are a = 20°, b = 130° and c = 50°
(ii) In ∆PQS, we have
∠a + 60° + 55° = 180°(Angle sum property)
⇒ ∠a + 115° = 180°
⇒ ∠a = 180° – 115°
⇒ ∠a = 65°
∠a + ∠b = 180° (Linear pair)
⇒ 65° + ∠b = 180°
⇒ ∠b = 180° – 65° = 115°
In ∆PSR, we have
∠b + ∠c + 40° = 180° (Angle sum property)
⇒ 115° + ∠c + 40° = 180°
⇒ ∠c + 155° = 180°
⇒ ∠c = 180° – 155° = 25°
Hence, the required angles are a = 65°, b = 115° and c = 25°
Q3: I have three sides. One of my angle measure 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
Sol:
Since I have three sides.
It is a triangle i.e. three-sided polygon.
Two angles are 15° and 60°.
Third angle = 180° – (15° + 60°)
= 180° – 75° (Angle sum property)
= 105°
which is greater than 90°.
Hence, it is an obtuse triangle.
Q4: An iron rod 5m long is placed against the wall in such a way that the foot of the rod is 3m away from the wall. Find how high the top of the iron rod reaches in the wall ?
Sol: 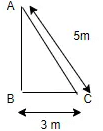
AC2 = BC2 + AB2
25 = AB2 + 9
AB2 = 16
AB = 4 m
Q5: Here in the given figure ∠BAC = 90º , ∠ABC = 65º, AD⊥BC. Find p and q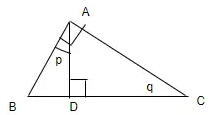
Sol:
In ΔABC
∠ABC + q + 90 = 180
q = 90 − 65 = 25º
In ΔABD
∠ABD + p + 90 = 180
p = 25º
Q6: Find the value of a,b and c in the below figures
(i) (ii)
(ii)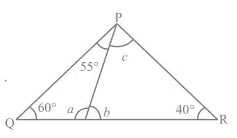 Sol:
Sol:
(i) In Δ ABC
a + ( 60+30 ) + 70 = 180
a + 90 + 70 = 180
a = 20°
Also
a + 30 + b = 180
b = 130°
Also
60 + c + 70 = 180
c = 50°
(ii) In ΔABC
55 + c + 60 + 40 = 180
c = 25°
Now
25 + b + 40 = 180
b = 115°
Now
a + 60 + 55 = 180
a = 65°
Q7: One of the exterior angles of a triangle is 120° and the interior opposite angles of it are in the ratio 4 : 2. Find the angles of the triangle.
Sol:
Let the angles be 4x and 2x
Then
4x + 2 x =120
x= 20
So angles are 80°,40°,60°
Q8: From the adjoining figure, find the value of x and also the measures of ∠P , ∠Q and ∠R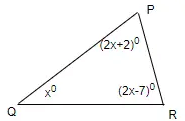 Sol:
Sol:
2x + 2 + x + 2x − 7 = 180
5x = 185
x = 37º
So angles are 76°, 37°,67°
Q9: Find the measures of ∠x and ∠y.
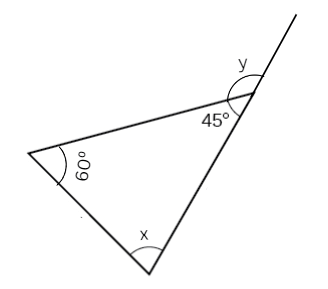 Sol:
Sol:
First
60 + 45 + x = 180
x = 75°
Now
y = x+ 60
= 75 + 60 = 135°
|
77 videos|386 docs|39 tests
|
FAQs on Class 7 Maths Chapter 6 HOTS Questions - The Triangle and Its Properties
| 1. What are the properties of triangles? |  |
| 2. What are the types of triangles based on their angles? |  |
| 3. What are the types of triangles based on their sides? |  |
| 4. How can we find the area of a triangle? |  |
| 5. How can we determine if three given side lengths form a triangle? |  |






















