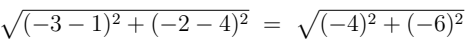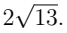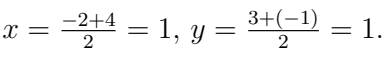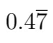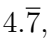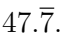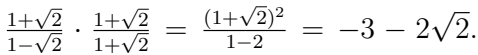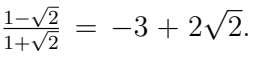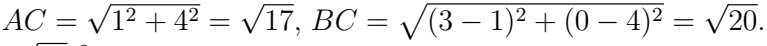Half Yearly Class 9 Mathematics Set 1 (Solutions) | Mathematics (Maths) Class 9 PDF Download
Time: 3 Hours
Maximum Marks: 80
General Instructions:
(i) The question paper comprises four sections: A, B, C, and D.
(ii) All questions are compulsory. However, internal choices are provided in some questions.
(iii) Section A has 10 Questions carrying 1 mark each.
(iv) Section B has 5 Questions carrying 2 marks each.
(v) Section C has 10 Questions carrying 3 marks each.
(vi) Section D has 5 Questions carrying 6 marks each.
(vii) Use of calculators is not permitted.
Section A
Q1. Express  as a fraction. (1 Mark)
as a fraction. (1 Mark)
Ans: Let
Then, 10x =
Subtract: 10x − x =
⇒ 9x = 6
⇒ x = 6/9 = 2/3.
Q2. Find the degree of the polynomial 3x4 − 5x2 + 2. (1 Mark)
Ans: Degree of 3x4 − 5x2 + 2 is 4.
Q3. Write the coordinates of the point where the x-axis and y-axis intersect. (1 Mark)
Ans: The x-axis and y-axis intersect at the origin, (0, 0).
Q4. In ax + by + c = 0, what is b if the line is parallel to the x-axis? (1 Mark)
Ans: For a line parallel to the x-axis, y = k, so in ax + by + c = 0, b ≠ 0, a = 0.
Q5. State Euclid’s second postulate. (1 Mark)
Ans: Euclid’s second postulate: Any straight line segment can be extended indefinitely in a straight line.
Q6. If one angle of a triangle is 80and the other two are equal, find each equal angle. (1 Mark)
Ans: Let each equal angle be x. Then, x + x + 80° = 180°
⇒ 2 = 100°
⇒ x = 50°
Q7. Simplify: √18. (1 Mark)
Ans:
Q8. If (x − 3) is a factor of x2 − 5x + k, find k. (1 Mark)
Ans: If (x − 3) is a factor, p(3) = 0.
So, 32 − 5 · 3 + k = 0
⇒ 9 − 15 + k = 0
⇒ k = 6.
Q9. In which quadrant does the point (2, −5) lie? (1 Mark)
Ans: Point (2, −5) has x > 0, y < 0, so it lies in the fourth quadrant.
Q10. If two lines intersect, what is the measure of a pair of vertically opposite angles? (1 Mark)
Ans: Vertically opposite angles are equal.
Section B
Q1. Rationalize the denominator: 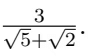 (2 Marks)
(2 Marks)
Ans:
Q2. Find the remainder when p(x) = x3 − 4x2 + 6x − 1 is divided by x − 2. (2 Marks)
Ans: For p(x) = x3 − 4x2 + 6x − 1, remainder is p(2) = 23 − 4·22 + 6·2−1 = 8 − 16 + 12 − 1 = 3.
Q3. Find the distance between points P (1, 4) and Q(−3, −2). (2 Marks)
Ans: Distance:
Q4. Solve 3x + 2y = 10 for y when x = 2. (2 Marks)
Ans: For 3x + 2y = 10, when x = 2: 3 · 2 + 2y = 10
⇒ 6 + 2y = 10
⇒ 2y = 4
⇒ y = 2.
Q5. If two angles on a straight line are (2x + 10)° and (x − 10)°, find x. (2 Marks)
Ans: (2x + 10)° + (x − 10)° = 180°
⇒ 3x = 180
⇒ x = 60.
Section C
Q1. Prove that √3 is irrational. (3 Marks)
Ans: Assume √3 = a/b, a, b coprime, b ≠ 0.
Then, 3 = a2/b2 ⇒ a2 = 3b2
So, 3 divides a2, hence a.
Let a = 3k. Then, 9k2 = 3b2
⇒ b2 = 3k2, so 3 divides b. Contradiction.
Q2. Using factor theorem, show that (x + 1) is a factor of x3 + x2 − 2x − 2. (3 Marks)
Ans: For p(x) = x3 + x2 − 2x − 2, p(−1) = (−1)3 + (−1)2 − 2(−1) − 2 = −1 + 1 + 2 − 2 = 0.
So, (x + 1) is a factor.
Q3. Find the coordinates of the midpoint of the line segment joining A(−2, 3) and B(4, −1). (3 Marks)
Ans: Midpoint of A(−2, 3), B(4, −1):
Q4. Solve: x + y = 5 and 2x − y = 4 using substitution method. (3 Marks)
Ans: From x + y = 5, y = 5 − x.
Substitute in 2x − y = 4: 2x − (5 − x) = 4
⇒ 3x − 5 = 4
⇒ 3x = 9
⇒ x = 3, y = 5 − 3 = 2.
Q5. Using Euclid’s postulates, prove that a line segment can be drawn joining any two points. (3 Marks)
Ans: Euclid’s first postulate: A straight line can be drawn joining any two points. Proof follows directly.
Q6. In △PQR, ∠P = 50°, ∠Q = 70°. Find ∠R. If ST ∥ QR, find ∠P ST. (3 Marks)
Ans: ∠R = 180° - (50° + 70°) = 60°
Since ST ∥ QR, ∠PST = ∠PQR = 70° (corresponding angles).
Q7. Find k such that x2 + kx + 4 has equal roots. (3 Marks)
Ans: Discriminant: k2 − 4 · 1 · 4 = 0
⇒ k2 = 16
⇒ k = ±4.
Q8. Express 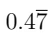 as a fraction. (3 Marks)
as a fraction. (3 Marks)
Ans: Let x =
Then, 10x =
100x =Subtract: 100x−10x =
⇒ 90x = 43
⇒ x = 43/90.
Q9. Simplify: 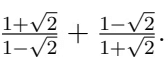 (3 Marks)
(3 Marks)
Ans:
Similarly,
Sum:
Q10. Solve: 4x − y = 8 and 2x + y = 7 using substitution method. (3 Marks)
Ans: From 4x − y = 8, y = 4x − 8.
Substitute in 2x + y = 7: 2x + (4x − 8) = 7
⇒ 6x = 15
⇒ x = 5/2, y = 4· 5/2 - 8 = 2.
Section D
Q1. Factorize x3 − 7x + 14x − 8 completely. (6 Marks)
Ans: For p(x) = x3 −7x2 + 14x − 8, p(1) = 1−7+14−8 = 0, so (x−1) is a factor.
Synthetic division: 1, −7, 14, −8 with root 1: 1, 1 − 6, −6 + 8, 2 − 8
⇒ x2 − 6x + 8. Factorize: (x − 2)(x − 4).
Thus, p(x) = (x − 1)(x − 2)(x − 4).
Q2. In the coordinate plane, find the area of △ABC with vertices A(0, 0), B(3, 0), C (1, 4). Is it a right-angled triangle? (6 Marks)
Ans: Area: 1/2 |0(0 − 4) + 3(4 − 0) + 1(0 − 0)| = 1/2|12| = 6 sq.
units. Sides: AB = 3,
Check: 32 + (√17)2 ≠ (√20)2 not right-angled.
Q3. Prove that vertically opposite angles are equal when two lines intersect. Use this to show that the sum of angles in a triangle is 180°. (6 Marks)
Ans: Let lines AB and C D intersect at O.
∠AOC = ∠BOD (same arcs).
For triangle, extend BC to D, draw C E ∥ AB.
∠BAC = ∠ACE, ∠ABC = ∠BCE (corresponding).
∠ACE + ∠ACB, ∠BCE = 180°, so ∠BAC + ∠ABC + ∠ACB = 180°
Q4. Solve graphically: x + y = 6 and 2x − y = 3. Find the area of the triangle formed by these lines and the y-axis. (6 Marks)
Ans: For x + y = 6: (6, 0), (0, 6).
For 2x − y = 3: (3, 3), (0, −3).
Intersection: x = 3, y = 3
Triangle vertices: (0, −3), (0, 6), (3, 3).
Area: 1/2 · 3 · 9 = 13.5 sq. units.
Q5. Solve: 2x + 3y = 11 and x − 2y = −2 using elimination method. Verify the solution. (6 Marks)
Ans: Multiply second equation by 2: 2x − 4y = −4.
Add to first: 2x + 3y + 2x − 4y = 11 − 4
⇒ 4x−y = 7.
Solve with x−2y = −2: x = 3, y = 5/2
Verify: 2·3 + 3· 5/2 = 11, 3−2·5/2 = - 2.
|
40 videos|471 docs|57 tests
|
FAQs on Half Yearly Class 9 Mathematics Set 1 (Solutions) - Mathematics (Maths) Class 9
| 1. What topics are commonly covered in a Class 9 Half-Yearly Math exam? |  |
| 2. How can I prepare effectively for the Half-Yearly Math exam? |  |
| 3. What is the format of the Half-Yearly Math Question Paper? |  |
| 4. How important is time management during the Half-Yearly Math exam? |  |
| 5. What resources can help students excel in their Class 9 Math exam? |  |