Handshaking Lemma | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
Handshaking Theorem is also known as Handshaking Lemma or Sum of Degree Theorem.
In Graph Theory,
Handshaking Theorem states in any given graph,
Sum of degree of all the vertices is twice the number of edges contained in it.
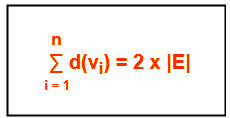
Handshaking Theorem
The following conclusions may be drawn from the Handshaking Theorem.
In any graph,
- The sum of degree of all the vertices is always even.
- The sum of degree of all the vertices with odd degree is always even.
- The number of vertices with odd degree are always even.
Practice Problems Based on Handshaking Theorem in Graph Theory
Problem 1: A simple graph G has 24 edges and degree of each vertex is 4. Find the number of vertices.
Given
- Number of edges = 24
- Degree of each vertex = 4
Let number of vertices in the graph = n.
Using Handshaking Theorem, we have
Sum of degree of all vertices = 2 x Number of edges
Substituting the values, we get
n x 4 = 2 x 24
n = 2 x 6
∴ n = 12
Thus, Number of vertices in the graph = 12.
Problem 2: A graph contains 21 edges, 3 vertices of degree 4 and all other vertices of degree 2. Find total number of vertices.
Given
- Number of edges = 21
- Number of degree 4 vertices = 3
- All other vertices are of degree 2
Let number of vertices in the graph = n.
Using Handshaking Theorem, we have
Sum of degree of all vertices = 2 x Number of edges
Substituting the values, we get-
3 x 4 + (n-3) x 2 = 2 x 21
12 + 2n – 6 = 42
2n = 42 – 6
2n = 36
∴ n = 18
Thus, Total number of vertices in the graph = 18.
Problem 3: A simple graph contains 35 edges, four vertices of degree 5, five vertices of degree 4 and four vertices of degree 3. Find the number of vertices with degree 2.
Given
- Number of edges = 35
- Number of degree 5 vertices = 4
- Number of degree 4 vertices = 5
- Number of degree 3 vertices = 4
Let number of degree 2 vertices in the graph = n.
Using Handshaking Theorem, we have
Sum of degree of all vertices = 2 x Number of edges
Substituting the values, we get
4 x 5 + 5 x 4 + 4 x 3 + n x 2 = 2 x 35
20 + 20 + 12 + 2n = 70
52 + 2n = 70
2n = 70 – 52
2n = 18
∴ n = 9
Thus, Number of degree 2 vertices in the graph = 9.
Problem 4: A graph has 24 edges and degree of each vertex is k, then which of the following is possible number of vertices?
(a) 20
(b) 15
(c) 10
(d) 8
Given
- Number of edges = 24
- Degree of each vertex = k
Let number of vertices in the graph = n.
Using Handshaking Theorem, we have
Sum of degree of all vertices = 2 x Number of edges
Substituting the values, we get-
n x k = 2 x 24
k = 48 / n
Now,
- It is obvious that the degree of any vertex must be a whole number.
- So in the above equation, only those values of ‘n’ are permissible which gives the whole value of ‘k’.
Now, let us check all the options one by one
- For n = 20, k = 2.4 which is not allowed.
- For n = 15, k = 3.2 which is not allowed.
- For n = 10, k = 4.8 which is not allowed.
- For n = 8, k = 6 which is allowed.
Thus, Option (D) is correct.
|
65 videos|129 docs|94 tests
|





















