The observables discussed so far have had discrete sets of experimental values. For example, the values of the energy of a bound system are always discrete, and angular momentum components have values that take the form mℏ, where m is either an integer or a half-integer, positive or negative. On the other hand, the position of a particle or the linear momentum of a free particle can take continuous values in both quantum and classical theory. The mathematics of observables with a continuous spectrum of measured values is somewhat more complicated than for the discrete case but presents no problems of principle. An observable with a continuous spectrum of measured values has an infinite number of state functions. The state function Ψ of the system is still regarded as a combination of the state functions of the observable, but the sum in equation (10) must be replaced by an integral.
Measurements can be made of position x of a particle and the x-component of its linear momentum, denoted by px. These two observables are incompatible because they have different state functions. The phenomenon of diffraction noted above illustrates the impossibility of measuring position and momentum simultaneously and precisely. If a parallel monochromatic light beam passes through a slit (Figure 4A), its intensity varies with direction, as shown in Figure 4B. The light has zero intensity in certain directions. Wave theory shows that the first zero occurs at an angle θ0, given by sin θ0 = λ/b, where λ is the wavelength of the light and b is the width of the slit. If the width of the slit is reduced, θ0 increases—i.e., the diffracted light is more spread out. Thus, θ0 measures the spread of the beam.
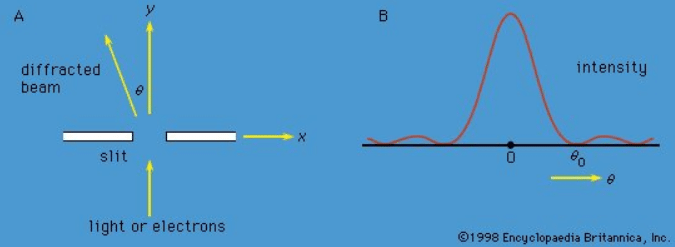 Figure 4: (A) Parallel monochromatic light incident normally on a slit, (B) variation in the intensity of the light with direction after it has passed through the slit. If the experiment is repeated with electrons instead of light, the same diagram would represent the variation in the intensity (i.e., relative number) of the electrons.
Figure 4: (A) Parallel monochromatic light incident normally on a slit, (B) variation in the intensity of the light with direction after it has passed through the slit. If the experiment is repeated with electrons instead of light, the same diagram would represent the variation in the intensity (i.e., relative number) of the electrons.
The experiment can be repeated with a stream of electrons instead of a beam of light. According to de Broglie, electrons have wavelike properties; therefore, the beam of electrons emerging from the slit should widen and spread out like a beam of light waves. This has been observed in experiments. If the electrons have velocity u in the forward direction (i.e., the y-direction in Figure 4A), their (linear) momentum is p = meu. Consider px, the component of momentum in the x-direction. After the electrons have passed through the aperture, the spread in their directions results in an uncertainty in px by an amount
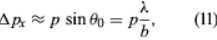
where λ is the wavelength of the electrons and, according to the de Broglie formula, equals h/p. Thus, Δpx ≈ h/b. Exactly where an electron passed through the slit is unknown; it is only certain that an electron went through somewhere. Therefore, immediately after an electron goes through, the uncertainty in its x-position is Δx ≈ b/2. Thus, the product of the uncertainties is of the order of ℏ. More exact analysis shows that the product has a lower limit, given by
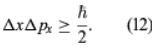
This is the well-known Heisenberg uncertainty principle for position and momentum. It states that there is a limit to the precision with which the position and the momentum of an object can be measured at the same time. Depending on the experimental conditions, either quantity can be measured as precisely as desired (at least in principle), but the more precisely one of the quantities is measured, the less precisely the other is known.
The uncertainty principle is significant only on the atomic scale because of the small value of h in everyday units. If the position of a macroscopic object with a mass of, say, one gram is measured with a precision of 10−6 metre, the uncertainty principle states that its velocity cannot be measured to better than about 10−25 metre per second. Such a limitation is hardly worrisome. However, if an electron is located in an atom about 10−10 metre across, the principle gives a minimum uncertainty in the velocity of about 106 metre per second.
The above reasoning leading to the uncertainty principle is based on the wave-particle duality of the electron. When Heisenberg first propounded the principle in 1927 his reasoning was based, however, on the wave-particle duality of the photon. He considered the process of measuring the position of an electron by observing it in a microscope. Diffraction effects due to the wave nature of light result in a blurring of the image; the resulting uncertainty in the position of the electron is approximately equal to the wavelength of the light. To reduce this uncertainty, it is necessary to use light of shorter wavelength—e.g., gamma rays. However, in producing an image of the electron, the gamma-ray photon bounces off the electron, giving the Compton effect (see above Early developments: Scattering of X-rays). As a result of the collision, the electron recoils in a statistically random way. The resulting uncertainty in the momentum of the electron is proportional to the momentum of the photon, which is inversely proportional to the wavelength of the photon. So it is again the case that increased precision in knowledge of the position of the electron is gained only at the expense of decreased precision in knowledge of its momentum. A detailed calculation of the process yields the same result as before (equation [12]). Heisenberg’s reasoning brings out clearly the fact that the smaller the particle being observed, the more significant is the uncertainty principle. When a large body is observed, photons still bounce off it and change its momentum, but, considered as a fraction of the initial momentum of the body, the change is insignificant.
The Schrödinger and Dirac theories give a precise value for the energy of each stationary state, but in reality the states do not have a precise energy. The only exception is in the ground (lowest energy) state. Instead, the energies of the states are spread over a small range. The spread arises from the fact that, because the electron can make a transition to another state, the initial state has a finite lifetime. The transition is a random process, and so different atoms in the same state have different lifetimes. If the mean lifetime is denoted as τ, the theory shows that the energy of the initial state has a spread of energy ΔE, given by
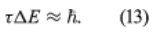 This energy spread is manifested in a spread in the frequencies of emitted radiation. Therefore, the spectral lines are not infinitely sharp. (Some experimental factors can also broaden a line, but their effects can be reduced; however, the present effect, known as natural broadening, is fundamental and cannot be reduced.) Equation (13) is another type of Heisenberg uncertainty relation; generally, if a measurement with duration τ is made of the energy in a system, the measurement disturbs the system, causing the energy to be uncertain by an amount ΔE, the magnitude of which is given by the above equation.
This energy spread is manifested in a spread in the frequencies of emitted radiation. Therefore, the spectral lines are not infinitely sharp. (Some experimental factors can also broaden a line, but their effects can be reduced; however, the present effect, known as natural broadening, is fundamental and cannot be reduced.) Equation (13) is another type of Heisenberg uncertainty relation; generally, if a measurement with duration τ is made of the energy in a system, the measurement disturbs the system, causing the energy to be uncertain by an amount ΔE, the magnitude of which is given by the above equation.
 Figure 4: (A) Parallel monochromatic light incident normally on a slit, (B) variation in the intensity of the light with direction after it has passed through the slit. If the experiment is repeated with electrons instead of light, the same diagram would represent the variation in the intensity (i.e., relative number) of the electrons.
Figure 4: (A) Parallel monochromatic light incident normally on a slit, (B) variation in the intensity of the light with direction after it has passed through the slit. If the experiment is repeated with electrons instead of light, the same diagram would represent the variation in the intensity (i.e., relative number) of the electrons.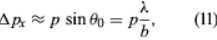
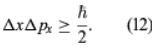
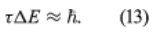 This energy spread is manifested in a spread in the frequencies of emitted radiation. Therefore, the spectral lines are not infinitely sharp. (Some experimental factors can also broaden a line, but their effects can be reduced; however, the present effect, known as natural broadening, is fundamental and cannot be reduced.) Equation (13) is another type of Heisenberg uncertainty relation; generally, if a measurement with duration τ is made of the energy in a system, the measurement disturbs the system, causing the energy to be uncertain by an amount ΔE, the magnitude of which is given by the above equation.
This energy spread is manifested in a spread in the frequencies of emitted radiation. Therefore, the spectral lines are not infinitely sharp. (Some experimental factors can also broaden a line, but their effects can be reduced; however, the present effect, known as natural broadening, is fundamental and cannot be reduced.) Equation (13) is another type of Heisenberg uncertainty relation; generally, if a measurement with duration τ is made of the energy in a system, the measurement disturbs the system, causing the energy to be uncertain by an amount ΔE, the magnitude of which is given by the above equation.


























