Hilbert space:- Normed vector space | Additional Topics for IIT JAM Mathematics PDF Download
Motivating example: Euclidean space:-
One of the most familiar examples of a Hilbert space is the Euclidean space consisting of three-dimensional vectors, denoted by ℝ3, and equipped with the dot product. The dot product takes two vectors x and y, and produces a real number x · y. If x and y are represented in Cartesian coordinates, then the dot product is defined by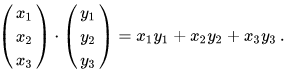
The dot product satisfies the properties:
- It is symmetric in x and y: x · y = y · x.
- It is linear in its first argument: (ax1 + bx2) · y = ax1 · y + bx2 . y for any scalars a, b, and vectors x1, x2, and y.
- It is positive definite: for all vectors x, x · x ≥ 0 , with equality if and only if x = 0.
An operation on pairs of vectors that, like the dot product, satisfies these three properties is known as a (real) inner product. A vector space equipped with such an inner product is known as a (real) inner product space. Every finite-dimensional inner product space is also a Hilbert space. The basic feature of the dot product that connects it with Euclidean geometry is that it is related to both the length (or norm) of a vector, denoted ||x||, and to the angle θ between two vectors x and y by means of the formula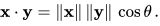
Multivariable calculus in Euclidean space relies on the ability to compute limits, and to have useful criteria for concluding that limits exist. A mathematical series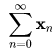
consisting of vectors in ℝ3 is absolutely convergent provided that the sum of the lengths converges as an ordinary series of real numbers:
Just as with a series of scalars, a series of vectors that converges absolutely also converges to some limit vector L in the Euclidean space, in the sense that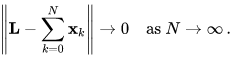

This property expresses the completeness of Euclidean space: that a series that converges absolutely also converges in the ordinary sense.
Hilbert spaces are often taken over the complex numbers. The complex plane denoted by ℂ is equipped with a notion of magnitude, the complex modulus |z| which is defined as the square root of the product of z with its complex conjugate:
If z = x + iy is a decomposition of z into its real and imaginary parts, then the modulus is the usual Euclidean two-dimensional length: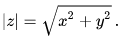
The inner product of a pair of complex numbers z and w is the product of z with the complex conjugate of w: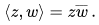
This is complex-valued. The real part of ⟨z, w⟩ gives the usual two-dimensional Euclidean dot product.
A second example is the space ℂ2 whose elements are pairs of complex numbers z = (z1, z2). Then the inner product of z with another such vector w = (w1, w2) is given by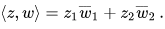
The real part of ⟨z, w⟩ is then the four-dimensional Euclidean dot product. This inner product is Hermitian symmetric, which means that the result of interchanging z and w is the complex conjugate: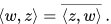
Definition:- A Hilbert space H is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product.
To say that H is a complex inner product space means that H is a complex vector space on which there is an inner product ⟨x, y⟩ associating a complex number to each pair of elements x, y of H that satisfies the following properties:
- The inner product is conjugate symmetric; that is, the inner product of a pair of elements is equal to the complex conjugate of the inner product of the swapped elements:
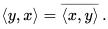
- The inner product is linear in its first[nb 1] argument. For all complex numbers a and b
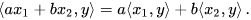
- The inner product of an element with itself is positive definite:
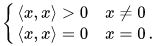
It follows from properties 1 and 2 that a complex inner product is conjugate linear in its second argument, meaning that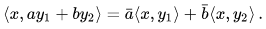
A real inner product space is defined in the same way, except that H is a real vector space and the inner product takes real values. Such an inner product will be bilinear: that is, linear in each argument.
The norm is the real-valued function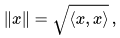
and the distance d between two points x, y in H is defined in terms of the norm by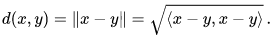
That this function is a distance function means firstly that it is symmetric in x and y, secondly that the distance between x and itself is zero, and otherwise the distance between x and y must be positive, and lastly that the triangle inequality holds, meaning that the length of one leg of a triangle xyz cannot exceed the sum of the lengths of the other two legs: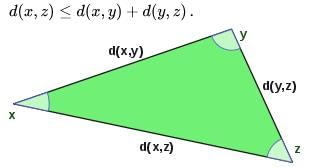
This last property is ultimately a consequence of the more fundamental Cauchy–Schwarz inequality, which asserts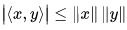
with equality if and only if x and y are linearly dependent.
With a distance function defined in this way, any inner product space is a metric space, and sometimes is known as a pre-Hilbert space. Any pre-Hilbert space that is additionally also a complete space is a Hilbert space.
The completeness of H is expressed using a form of the Cauchy criterion for sequences in H: a pre-Hilbert space H is complete if every Cauchy sequence converges with respect to this norm to an element in the space. Completeness can be characterized by the following equivalent condition: if a series of vectors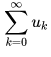
converges absolutely in the sense that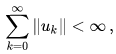
then the series converges in H, in the sense that the partial sums converge to an element of H.
As a complete normed space, Hilbert spaces are by definition also Banach spaces. As such they are topological vector spaces, in which topological notions like the openness and closedness of subsets are well defined. Of special importance is the notion of a closed linear subspace of a Hilbert space that, with the inner product induced by restriction, is also complete (being a closed set in a complete metric space) and therefore a Hilbert space in its own right.
Second example: sequence spaces:-
The sequence space l2 consists of all infinite sequences z = (z1, z2, …) of complex numbers such that the series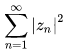
converges. The inner product on l2 is defined by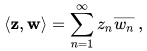
with the latter series converging as a consequence of the Cauchy–Schwarz inequality.
Completeness of the space holds provided that whenever a series of elements from l2 converges absolutely (in norm), then it converges to an element of l2. The proof is basic in mathematical analysis, and permits mathematical series of elements of the space to be manipulated with the same ease as series of complex numbers (or vectors in a finite-dimensional Euclidean space).
Examples:-
Lebesgue spaces:
Main article: Lp space
Lebesgue spaces are function spaces associated to measure spaces (X, M, μ), where X is a set, M is a σ-algebra of subsets of X, and μ is a countably additive measure on M. Let L2(X, μ) be the space of those complex-valued measurable functions on X for which the Lebesgue integral of the square of the absolute value of the function is finite, i.e., for a function f in L2(X, μ),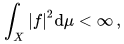
and where functions are identified if and only if they differ only on a set of measure zero.
The inner product of functions f and g in L2(X, μ) is then defined as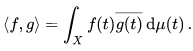
For f and g in L2, this integral exists because of the Cauchy–Schwarz inequality, and defines an inner product on the space. Equipped with this inner product, L2 is in fact complete. The Lebesgue integral is essential to ensure completeness: on domains of real numbers, for instance, not enough functions are Riemann integrable.
The Lebesgue spaces appear in many natural settings. The spaces L2(ℝ) and L2([0,1]) of square-integrable functions with respect to the Lebesgue measure on the real line and unit interval, respectively, are natural domains on which to define the Fourier transform and Fourier series. In other situations, the measure may be something other than the ordinary Lebesgue measure on the real line. For instance, if w is any positive measurable function, the space of all measurable functions f on the interval [0, 1] satisfying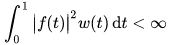
is called the weighted L2 space L2w([0, 1]), and w is called the weight function. The inner product is defined by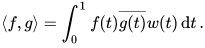
The weighted space L2w([0, 1]) is identical with the Hilbert space L2([0, 1], μ) where the measure μ of a Lebesgue-measurable set A is defined by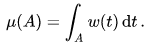
Weighted L2 spaces like this are frequently used to study orthogonal polynomials, because different families of orthogonal polynomials are orthogonal with respect to different weighting functions.
Spectral theory:- There is a well-developed spectral theory for self-adjoint operators in a Hilbert space, that is roughly analogous to the study of symmetric matrices over the reals or self-adjoint matrices over the complex numbers. In the same sense, one can obtain a "diagonalization" of a self-adjoint operator as a suitable sum (actually an integral) of orthogonal projection operators.
The spectrum of an operator T, denoted σ(T), is the set of complex numbers λ such that T − λ lacks a continuous inverse. If T is bounded, then the spectrum is always a compact set in the complex plane, and lies inside the disc |z| ≤ ||T||. If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m, M] where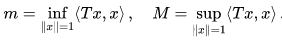
Moreover, m and M are both actually contained within the spectrum.
The eigenspaces of an operator T are given by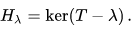
Unlike with finite matrices, not every element of the spectrum of T must be an eigenvalue: the linear operator T − λ may only lack an inverse because it is not surjective. Elements of the spectrum of an operator in the general sense are known as spectral values. Since spectral values need not be eigenvalues, the spectral decomposition is often more subtle than in finite dimensions.
However, the spectral theorem of a self-adjoint operator T takes a particularly simple form if, in addition, T is assumed to be a compact operator. The spectral theorem for compact self-adjoint operators states:
- A compact self-adjoint operator T has only countably (or finitely) many spectral values. The spectrum of T has no limit point in the complex plane except possibly zero. The eigenspaces of T decompose H into an orthogonal direct sum:
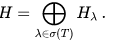
Moreover, if Eλ denotes the orthogonal projection onto the eigenspace Hλ, then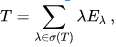
where the sum converges with respect to the norm on B(H). - This theorem plays a fundamental role in the theory of integral equations, as many integral operators are compact, in particular those that arise from Hilbert–Schmidt operators.
The general spectral theorem for self-adjoint operators involves a kind of operator-valued Riemann–Stieltjes integral, rather than an infinite summation. The spectral family associated to T associates to each real number λ an operator Eλ, which is the projection onto the nullspace of the operator (T − λ)+, where the positive part of a self-adjoint operator is defined by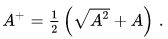
The operators Eλ are monotone increasing relative to the partial order defined on self-adjoint operators; the eigenvalues correspond precisely to the jump discontinuities. One has the spectral theorem, which asserts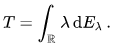
The integral is understood as a Riemann–Stieltjes integral, convergent with respect to the norm on B(H). In particular, one has the ordinary scalar-valued integral representation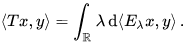
A somewhat similar spectral decomposition holds for normal operators, although because the spectrum may now contain non-real complex numbers, the operator-valued Stieltjes measure dEλ must instead be replaced by a resolution of the identity.
A major application of spectral methods is the spectral mapping theorem, which allows one to apply to a self-adjoint operator T any continuous complex function f defined on the spectrum of T by forming the integral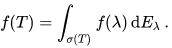
The resulting continuous functional calculus has applications in particular to pseudodifferential operators.
The spectral theory of unbounded self-adjoint operators is only marginally more difficult than for bounded operators. The spectrum of an unbounded operator is defined in precisely the same way as for bounded operators: λ is a spectral value if the resolvent operator fails to be a well-defined continuous operator. The self-adjointness of T still guarantees that the spectrum is real. Thus the essential idea of working with unbounded operators is to look instead at the resolvent Rλ where λ is nonreal. This is a bounded normal operator, which admits a spectral representation that can then be transferred to a spectral representation of T itself. A similar strategy is used, for instance, to study the spectrum of the Laplace operator: rather than address the operator directly, one instead looks as an associated resolvent such as a Riesz potential or Bessel potential.
fails to be a well-defined continuous operator. The self-adjointness of T still guarantees that the spectrum is real. Thus the essential idea of working with unbounded operators is to look instead at the resolvent Rλ where λ is nonreal. This is a bounded normal operator, which admits a spectral representation that can then be transferred to a spectral representation of T itself. A similar strategy is used, for instance, to study the spectrum of the Laplace operator: rather than address the operator directly, one instead looks as an associated resolvent such as a Riesz potential or Bessel potential.
A precise version of the spectral theorem in this case is:
Given a densely defined self-adjoint operator T on a Hilbert space H, there corresponds a unique resolution of the identity E on the Borel sets of ℝ, such that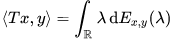
for all x ∈ D(T) and y ∈ H. The spectral measure E is concentrated on the spectrum of T.
There is also a version of the spectral theorem that applies to unbounded normal operators.
|
2 videos|45 docs|4 tests
|
















