How to Solve Exponential Equations using Logarithms | General Aptitude for GATE - Mechanical Engineering PDF Download
Steps to Solve Exponential Equations using Logarithms
- Keep the exponential expression by itself on one side of the equation.
- Get the logarithms of both sides of the equation. You can use any bases for logs.
- Solve for the variable. Keep the answer exact or give decimal approximations. In addition to the steps above, make sure that you review the Basic Logarithm Rules because you will use them in one way or another.

Examples of How to Solve Exponential Equations using Logarithms
Example 1: Solve the exponential equation 52x = 21.
Sol:
The good thing about this equation is that the exponential expression is already isolated on the left side. We can now take the logarithms of both sides of the equation. It doesn’t matter what base of the logarithm to use. The final answer should come out the same. The best choice for the base of log operation is 5 since it is the base of the exponential expression itself. However, we will also use in the calculation the common base of 10, and the natural base of e (denoted by ln) just to show that in the end, they all have the same answers.
Log Base of 5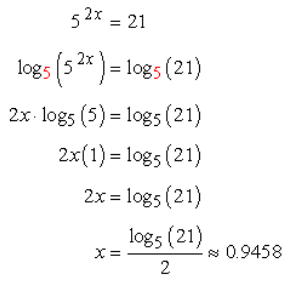
Log Base of 10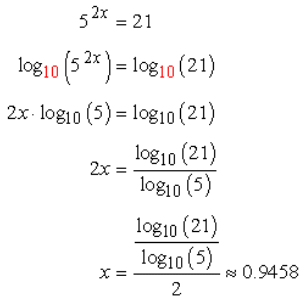
Log Base of e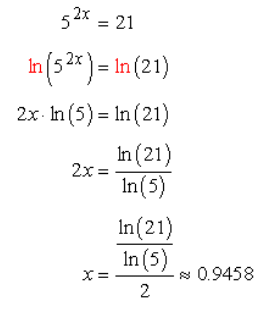
Example 2: Solve the exponential equation 2 (3x–5)=12.
Sol: As you can see, the exponential expression on the left is not by itself. We must eliminate the number 2 that is multiplying the exponential expression. To do that, divide both sides by 2. That would leave us just the exponential expression on the left, and 6 on the right after simplification.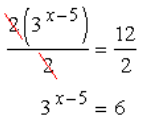
It’s time to take the log of both sides. Since the exponential expression has base 3, that’s the convenient base to use for log operation. In addition, we will also solve this using the natural base e just to compare if our final results agree.
Log Base of 3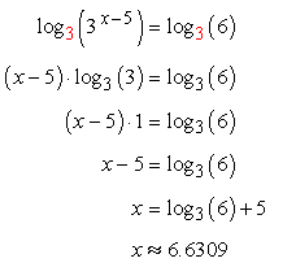
Log Base of e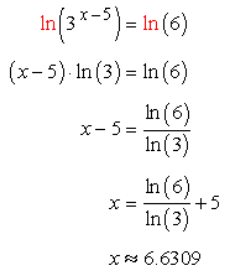
Example 3: Solve the exponential equation 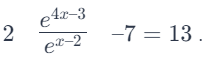
Sol:
This looks like a mess at first. However, if you know how to start this out, the solution to this problem becomes a breeze. What we should do first is to simplify the expression inside the parenthesis. Use the Division Rule of Exponent by copying the common base of e and subtracting the top by the bottom exponent.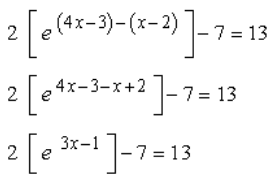
Now isolate the exponential expression by adding both sides by 7, followed by dividing the entire equation by 2.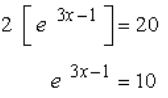
Take the logarithm of both sides. Use ln because we have a base of e. Then solve for the variable x.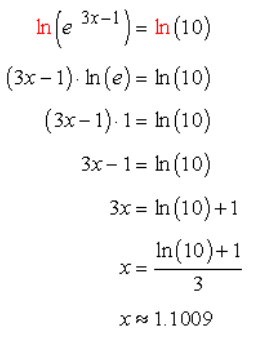
Example 4: Solve the exponential equation 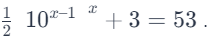
Sol:
Observe that the exponential expression is being raised to x. Simplify this by applying the Power to a Power Rule. Do that by copying the base 10 and multiplying its exponent to the outer exponent. It should look like this after doing so.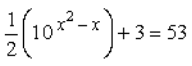
We can now isolate the exponential expression by subtracting both sides by 3 and then multiplying both sides by 2.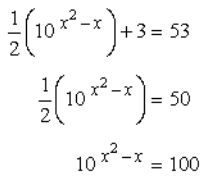
Take the logarithm of both sides with base 10. If you just see a log without any specific base, it is understood to have 10 as its base.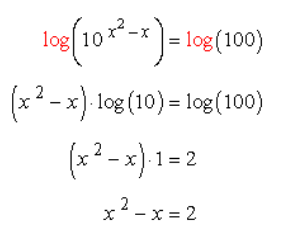
We are going to solve this quadratic equation by factoring method. Let’s move everything to the left side, therefore making the right side equal to zero. Factor out the trinomial into two binomials. Set each binomial factor equal zero then solve for x.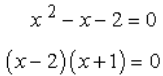
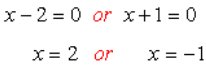
Example 5: Solve the exponential equation e2x –7ex +10 = 0.
Sol:
We will need a different strategy to solve this exponential equation. Observe that we can actually convert this into a factorable trinomial. First, we let m = ex. Rewrite the exponential expression using this substitution.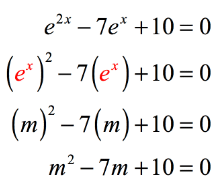
Factor out the trinomial as a product of two binomials. Then replace m m by ex again.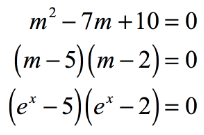
Finally, set each factor equal to zero and solve for x, as usual, using logarithms.
|
193 videos|169 docs|152 tests
|
















