Hydrostatic Force on Surfaces | Fluid Mechanics for Civil Engineering - Civil Engineering (CE) PDF Download
Fluid Statics
- Fluid Statics deals with fluids at rest while Fluid Dynamics studies fluids in motion.
- Any force developed is only due to normal stresses i.e, pressure. Such a condition is termed the hydrostatic condition.
- Fluid Statics is also known as Hydrostatics.
- A static fluid can have no shearing force acting on it, and that any force between the fluid and the boundary must be acting at right angles to the boundary.
- For an element of fluid at rest, the element will be in equilibrium. The sum of the components of forces in any direction will be zero. The sum of the moments of forces on the element about any point must also be zero.
- Within a fluid, the pressure is the same at all points in all directions.
- Pressure at the wall of any vessel is perpendicular to the wall.
- Pressure due to depth is P = ρgh and is the same at any horizontal level of connected fluid.
Fluid Pressure at a Point
- If a fluid is Stationary, then force acting on any surface or area is perpendicular to that surface.
- If the force exerted on each unit area of a boundary is the same, the pressure is said to be uniform
Pascal’s Law for Pressure At A Point
- It states that pressure or intensity of pressure at a point in a static fluid (fluid is in rest) is equal in all directions. If the fluid is not in motion then according to Pascal’s law,
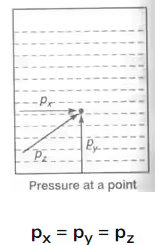
where, px, py and pz are the pressure at point x, y, z respectively.
General Equation For Variation Of Pressure in a Static Fluid
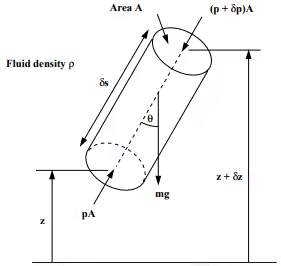
(A cylindrical element of fluid at an arbitrary orientation)
dp/ds = -ρgcosθ
Vertical Variation Of Pressure in a Fluid Under Gravity
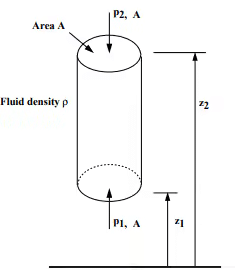
Taking upward as positive, we have
Vertical cylindrical element of fluid cross-sectional area = A
mass density = ρ
The forces involved are:
- Force due to p1 on A (upward) = p1. A
- Force due to p2 on A (downward) = p2. A
- Force due to weight of element (downward) = mg
= mass density x volume x g
= ρ.g.A.(z2 - z1)
Thus in a fluid under gravity, pressure decreases linearly with an increase in height
p2 - p1 = ρgA(z2 - z1) ⇧
This is the hydrostatic pressure change.
Equality Of Pressure At The Same Level In A Static Fluid
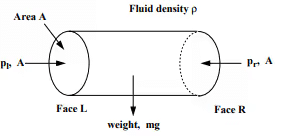 Horizontal cylindrical element cross-sectional area = A
Horizontal cylindrical element cross-sectional area = A
mass density =ρ
left end pressure = pl
right end pressure = or
For equilibrium, the sum of the forces in the x-direction is zero= pl. A = pr. A
pl = or
So, Pressure in the horizontal direction is constant.
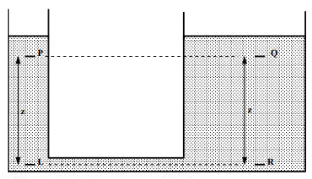
As we know, pl = pr
For a vertical pressure change we have
Pl = Pp + Pgz
and Pr = Pq + Pgz
so, Pp + Pgz = Pq + Pgz
Pp = Pq
Thus, pressure at the two equal levels is the same.
Total Hydrostatic Force on Plane Surfaces
- For horizontal plane, surface submerged in liquid, or plane surface inside a gas chamber, or any plane surface under the action of uniform hydrostatic pressure, the total hydrostatic force is given by
F = p . A
where p is the uniform pressure and A is the area. - In general, the total hydrostatic pressure on any plane surface is equal to the product of the area of the surface and the unit pressure at its center of gravity.
F = pcg . A
where pcg is the pressure at the center of gravity. - For homogeneous free liquid at rest, the equation can be expressed in terms of unit weight γ of the liquid.
F = γh'A
where h' is the depth of liquid above the centroid of the submerged area.
Derivation of Formulas
The figure shown below is an inclined plane surface submerged in a liquid. The total area of the plane surface is given by A, cg is the center of gravity, and cp is the center of pressure.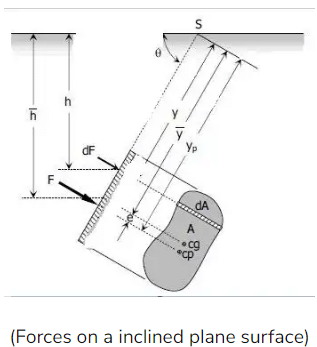
The differential force dF acting on the element dA is
dF = p . dA
dF = γ . h . dA
From the figure h = ysinθ,
dF = γ . (ysinθ) . dA
Integrate both sides and note that γ and θ are constants,
F = γ . sinθ . ∫y . dA
So, F = γ . sinθ . ∫y . dA
Recall from Calculus that
∫y . dA = A . y¯
Hence, F = (γ . sinθ)A . y¯
F = γ . (y¯sinθ) . A
From the figure, y¯sinθ = h¯, thus,
F = γh¯A
The product γh¯¯ is a unit pressure at the centroid at the plane area, thus, the formula can be expressed in a more general term below:
F = pcg . A
Location of Total Hydrostatic Force (Eccentricity)
From the figure above, S is the intersection of the prolongation of the submerged area to the free liquid surface. Taking moment about point S.
Fyp = ∫y. dF
Where dF = γ(ysinθ)dA
F = γ(y¯sinθ)A
[γ(y¯sinθ)A]yp = ∫y[γ(ysinθ)dA][γ(y¯sinθ)A]yp
= ∫y[γ(ysinθ)dA]
(γsinθ)Ay¯yp = (γsinθ)∫y2dA(γsinθ)Ay¯yp
= (γsinθ)∫y2dA
Ay¯yp = ∫y2dA
Again from Calculus, ∫y2dA is called the moment of inertia denoted by I Since our reference point is S,
Ay¯yp = IS
Thus, yp = IS/Ay¯
By transfer formula for the moment of inertia IS=Ig+Ay-2, the formula for yp will become
yp = (Ig+Ay-2)/Ay¯ or
yp = y¯+Ig/Ay¯
From the figure above, yp = y¯+e, thus, the distance between cg and cp is
Eccentricity, e = Ig/Ay¯
Example 1: An opening in a dam is covered with a plate of 1 m square and is hinged on the top and inclined at 60 0 to the horizontal. If the top edge of the gate is 2 m below the water level what is the force required to open the gate by pulling a chain set at 45 0 angle with the plate and set to the lower end of the plate. The plate weighs 2200 N.
Solution:
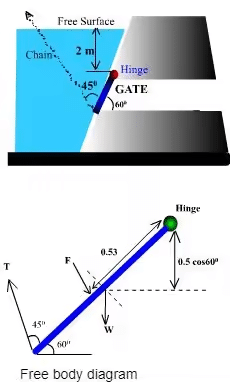
Given data: Area of the gate = 1m2
Total force on the gate = F = wAx̅
where x̅ = 2 + 1/2sin 60°
Depth of the center of pressure ħ = x̅ + lGsin2 60°/Ax̅
Distance of the application point of the force from the hinge = (ħ - 2) 1/sin60° = 0.53m
Taking moments about the hinge, T 1sin45° = F x 0.53 + 2200 x 1/2cos60°
Then, T = 18.66 kN
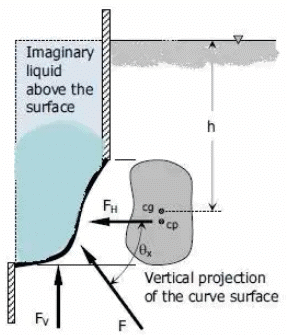
Total Hydrostatic Force on Curved Surfaces
- In the case of a curved surface submerged in liquid at rest, it is more convenient to deal with the horizontal and vertical components of the total force acting on the surface.
Note: The discussion here is also applicable to plane surfaces. - Horizontal Component: The horizontal component of the total hydrostatic force on any surface is equal to the pressure on the vertical projection of that surface.
FH = pcg . A - Vertical Component: The vertical component of the total hydrostatic force on any surface is equal to the weight of either real or imaginary liquid above it.
FV = γ . V - Total Hydrostatic Force:
F = √(FH2 + FV2) - Direction of F:
tanθx = FV / FH
Case 1: Liquid is above the curve surface
The vertical component of the hydrostatic force is downward and equal to the volume of the l

Case 2: Liquid is below the curve surface
The vertical component of the hydrostatic force is going upward and equal to the volume of the imaginary liquid above the surface.
Example 2: The length of a tainter gate is 1 m perpendicular to the plane of the paper. Find out the total horizontal force on the gate and the total hydrostatic force on the gate.
Solution:
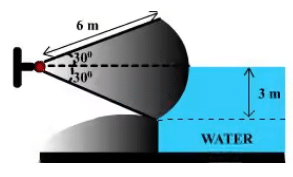
Horizontal hydrostatic force on the tainter gate
Fh = wAx̅ = 44.145 KN.
where projected area A = 3 x 1 = 3m2.
The vertical force is equal to the weight of water displaced by the shaded area.
The area of the shaded portion = π/12 x 62 - 1/2 x 3√3 x 3 = 1.63m2
The vertical force, Fv = 9810 x 1.63 x 1 = 15 99 KN.
The resultant force, 
and tanθ = Fv/Fh.
Answer: 46.95 KN and q = 19.9° With horizontal
Example 3: A quarter-circle (10 m diameter) gate which is 10 m wide perpendicular to the paper holds water as shown in the figure. Find the force required to hold the gate. The weight of the gate can be neglected.
Solution:
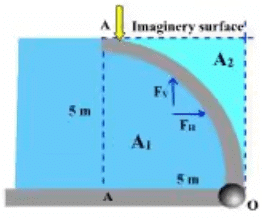
Horizontal force
FH = wAx̅
= 9810 x 5 x 10 x 5/2
=1226 MN
And it acts at a distance of 5/3 m from the bottom end.
And the upward vertical force is the weight of the Imaginary water body held over the plate.
Fv = 9810 x 10 x[52 - 1/4π52] = 5.26 x 105 N
And it will act through its C.G. which is Determined as follow -
C.G. of area A1 = 4R/3π = 20/3πm away from AA.
C.G. of the total area about AA is 2.5m away from AA.
C.G. of A2 => A1 x 20/3π + A2 x X = A x 2.5
x = 3.88m
Distance from ‘O' = (5 - 3.88) = 1.12m.
Taking moments about O => Fh x 5/3 + Fv x 1.12 = F x 5
Answer: 5.26 x105N
|
54 videos|127 docs|110 tests
|
FAQs on Hydrostatic Force on Surfaces - Fluid Mechanics for Civil Engineering - Civil Engineering (CE)
| 1. What is hydrostatic force on surfaces in civil engineering? |  |
| 2. How is hydrostatic force calculated on a submerged surface? |  |
| 3. What factors affect the magnitude of hydrostatic force on a surface in civil engineering? |  |
| 4. How does the hydrostatic force on a surface change with increasing depth of the fluid? |  |
| 5. Can hydrostatic force cause structural failure in civil engineering? |  |





















