Important Definitions & Formulas: Pair of Linear Equations in Two Variables | Mathematics (Maths) Class 10 PDF Download
The chapter on "Pair of Linear Equations in Two Variables" is very important because it teaches you how to deal with two equations that have variables in them. 
In this document, you'll find Class 10 Maths Formulas for Pair of Linear Equations in Two Variables, and these formulas can really help you do well in your board exams and future competitive exams.
Important Definitions
1. Equation: An equation is a statement that two mathematical expressions having one or more variables are equal.
2. Algebraic Equation: In algebra, an equation can be defined as a mathematical statement consisting of an equal symbol between two algebraic expressions that have the same value.
3. Linear Equation in Two Variables: The word 'Linear' means single degree equation i.e. the maximum powers of all the variables involved are one. The word 'Two Variables' means that the mathematical statement will be having two variables i.e. two mathematically unknown quantities.
The general form of a linear equation in two variables is ax+by+c=0, where a and b cannot be zero simultaneously.
Example: 2x+4y-8=0
Important Methods and Formulas
1. Algebraic Methods to solve Pair of Linear Equations in Two Variables
We have three algebraic methods of solution for a pair of linear equations in two variables:
(a) Substitution Method
Let’s solve the system of equations:
Step 1: Express y in terms of x from one of the equations.
From the first equation , solve for y:
y=5−2x
Step 2: Substitute this expression for y into the second equation.
3x Substitute y=5−2x into the second equation 3x−y=4:3x−(5−2x)=4
Simplify the equation:
3x−5+2x=4
5x−5=4
5x=9
x = 9/5
Step 3: Substitute the value of x back into the expression for y.
Substitute x = 9/5 into y = 5 - 2x
y = 5 - 2(9/5) = 5 - 18/5
= 25/5 - 18/5
= 7/5
Thus, the solution to the system of equation is:
x = 9/5, y = 7/5
(b) Elimination Method or Method of Elimination by Equating the Coefficients
Let’s solve the system of equations:
- 3x+2y=11
- 2x+3y=4
Step 1: Make the coefficients of one variable equal.
We will eliminate x by making the coefficients of x equal in both equations. Multiply the first equation by 2 and the second equation by 3, so that the coefficients of x become equal:
(Equation 1’)
(Equation 2’)
Step 2: Subtract one equation from the other to eliminate x.
Now subtract Equation 1' from Equation 2':
Step 3: Solve for y.
From , solve for y: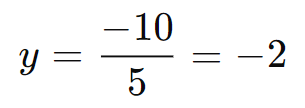
Step 4: Substitute the value of y into one of the original equations to find x.
Substitute into the first equation 3x+2y=11:
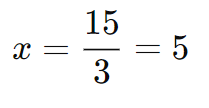
Solution:
Thus, the solution to the system of equations is:
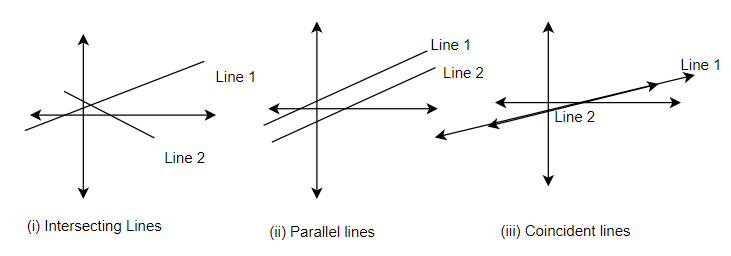
2. Conditions for Consistency/Inconsistency
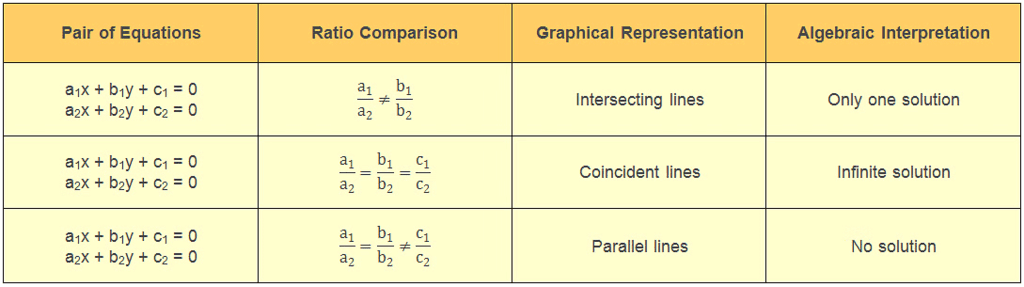 A pair of linear equations in two variables, which has a solution, is called consistent and a pair of linear equations in two variables, which has no solution is called inconsistent.
A pair of linear equations in two variables, which has a solution, is called consistent and a pair of linear equations in two variables, which has no solution is called inconsistent.
3. Steps to solve Word Problems
- Step 1: Read the statement carefully and identify the unknown quantities.
- Step 2: Represent the unknown quantity by x, y, z, a, b, c, etc.
- Step 3: Formulate the equations in terms of the variables to be determined and solve the equations to get the values of the required variables.
- Step 4: Finally, verify with the conditions of the original problem. The problems are stated in words, for this reason, often refers to word problems.
|
127 videos|584 docs|79 tests
|
FAQs on Important Definitions & Formulas: Pair of Linear Equations in Two Variables - Mathematics (Maths) Class 10
| 1. What is a pair of linear equations in two variables? |  |
| 2. How many solutions can a pair of linear equations in two variables have? |  |
| 3. What is the method to solve a pair of linear equations in two variables graphically? |  |
| 4. What is the substitution method for solving a pair of linear equations in two variables? |  |
| 5. How can we determine the consistency of a pair of linear equations in two variables? |  |

















