Important Formulae: Set Theory | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| What is a Set? |

|
| Types of Sets |

|
| Representation of Sets |

|
| Operations on Sets |

|
| Laws of Sets |

|
What is a Set?
A set refers to a group of clearly defined individual objects that come together to form a collection. This can include various items like numbers, days of the week, or types of vehicles. Each item within the set is known as an element. Sets are typically represented using curly braces.
For instance, a simple example of a set could be Set A = {1, 2, 3, 4, 5}. There are different ways to express the elements within a set.
Types of Sets
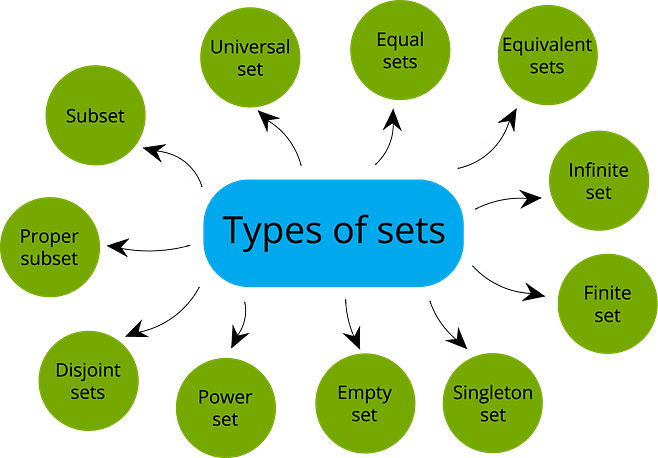
- Finite set: A finite set contains a limited number of elements. For example, a set of natural numbers up to 10, such as A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
- Infinite set: An infinite set includes an unlimited number of elements. For instance, a set of all natural numbers, represented as A = {1, 2, 3, ...}.
- Empty set: An empty set has no elements. For example, a set of apples in a basket of grapes is an empty set because there are no apples in a basket of grapes.
- Singleton set: A singleton set contains just one element. For instance, the set of only even prime numbers is {2}.
- Equal set: Two sets are considered equal if they contain the same elements. For example, A = {1, 2, 3, 4} and B = {4, 3, 2, 1}. In this case, A is equal to B.
- Equivalent set: Sets are equivalent when they have the same number of elements. For instance, A = {1, 2, 3, 4} and B = {Red, Blue, Green, Black} both have four elements, making them equivalent.
- Power set: A power set is the collection of all possible subsets of a set.
- Universal set: A universal set includes all sets being considered within a particular context. For example, if A = {1, 2, 3} and B = {2, 3, 4, 5}, the universal set would be U = {1, 2, 3, 4, 5}.
- Subset: Set A is considered a subset of Set B if every element of Set A is also present in Set B. If Set B contains at least one element not found in Set A, then Set A is a proper subset of Set B.
For example: A = {1,2,3}.
Thus, {1,2} is a subset of A.
Additional subsets of set A include: {1},{2},{3},{1,2},{2,3},{1,3},{1,2,3},{}.
A set with ‘n’ elements will have 2n subsets (2n – 1 proper subsets)
Did You Know?
The cardinal number of a set, denoted as n(A), represents the number of elements in the set. A set with a cardinal number of 0 is called a null set, while a set with a cardinal number of infinity (∞) is known as an infinite set.
Representation of Sets
1. Statement Form
- In this form, the members of the set are described in clear terms and placed within curly brackets.
- Example: If asked to write the set of even numbers less than 15, it would be expressed as {even numbers less than 15}.
2. Roster or Tabular Form
- In Roster form, every element of a set is listed explicitly.
- Example: To write the set of natural numbers less than 5, we first list the natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, ...
- The natural numbers less than 5 are 1, 2, 3, and 4.
- Therefore, the set can be shown as N = {1, 2, 3, 4}.

3. Set Builder Form
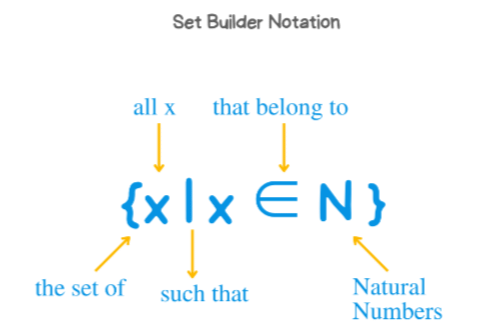
- This form uses a general structure where a set is defined by a property that its members satisfy.
- Example: For the set A = {2, 4, 6, 8}, we can express this in set builder form by noting that each number is 2 times a natural number.
- Thus, A can be written as A = {x: x=2n, n ∈ N and 1 ≤ n ≤ 4}, where n is a natural number between 1 and 4.
Operations on Sets
(I) Union
The union of sets A and B, denoted as A ∪ B, refers to the set of unique elements that are present in either set A, set B, or in both sets.
n(A U B) = n(A) + n(B) – n(A ∩ B) |
Here,
- n(A ∪ B) represents the total number of elements in the union of sets A and B, which is known as the cardinality of the set A ∪ B.
- n(A) denotes the number of elements in set A, referred to as the cardinality of set A.
- n(B) indicates the number of elements in set B, known as the cardinality of set B.
- n(C) signifies the number of elements in set C, termed as the cardinality of set C.
For three finite sets A, B, and C within a universal set U, the formula for the union is:
n(A∪B∪C)= n(A) +n(B) + n(C) - n(B⋂C) - n (A⋂ B)- n (A⋂C) + n(A⋂B⋂C) |
Example: Let U be a universal set consisting of all the natural numbers until 20 and set A and B be a subset of U defined as A = {2, 5, 9, 15, 19} and B = {8, 9, 10, 13, 15, 17}. Find A ∪ B.
Solution : We know, n(A U B) = n(A) + n(B) – n(A ∩ B)
Given, U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
A = {2, 5, 9, 15, 19}
B = {8, 9, 10, 13, 15, 17}
A ∪ B = {2, 5, 8, 9, 10, 13, 15, 17, 19}
(II) Intersection
The intersection of the sets A and B, denoted by A ∩ B, is the set of elements that belong to both A and B, i.e., the set of common elements in A and B.Example: If A = { 3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, and C = {11, 13, 15}, then find B ∩ C and A ∩ B ∩ C.
Ans: Given,
A = { 3, 5, 7, 9, 11} , B = {7, 9, 11, 13} , C = {11, 13, 15}
B ∩ C = {11, 13}
A ∩ B ∩ C = {11}
(III) Set Difference
The difference between sets is denoted as 'A - B'. This signifies the elements present in A that are not in B, encompassing all elements of A that exclude those in B.

Some properties related to the difference of sets are listed below:
- When two sets A and B are identical, then A – B = A – A = Ø (empty set) and B – A = B – B = Ø.
- The difference between any set and an empty set is the set itself, i.e., A – Ø = A.
- The difference of an empty set from any set results in an empty set, i.e., Ø – A = Ø.
- The difference of a set, say A, from the universal set U equals the empty set, i.e., A – U = Ø.
- If a superset is subtracted from a subset, the outcome is an empty set; that is, A – B = Ø if A ⊂ B.
- If A and B are disjoint sets (with no common elements), then A – B = A and B – A = B.
Example : If X = {11, 12, 13, 14, 15}, Y = {10, 12, 14, 16, 18} and Z = {7, 9, 11, 14, 18, 20}, then find the following:
(i) X – Y – Z
(ii) Y – X – Z
(iii) Z – X – Y
Ans: Given,
X = {11, 12, 13, 14, 15}
Y = {10, 12, 14, 16, 18}
Z = {7, 9, 11, 14, 18, 20}
(i) X – Y – Z = {11, 12, 13, 14, 15} – {10, 12, 14, 16, 18} – {7, 9, 11, 14, 18, 20}
= {13, 15}
(ii) Y – X – Z = {10, 12, 14, 16, 18} – {11, 12, 13, 14, 15} – {7, 9, 11, 14, 18, 20}
= {10, 16}
(iii) Z – X – Y = {7, 9, 11, 14, 18, 20} – {11, 12, 13, 14, 15} – {10, 12, 14, 16, 18}
= {7, 9, 20}
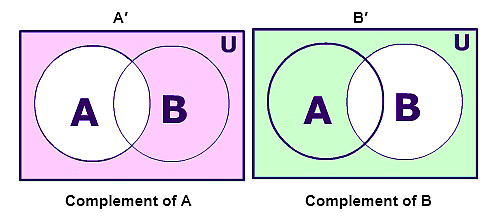
(IV) Complement of a Set
The complement of a set A, denoted as A C , consists of all the elements that are not present in A. It is calculated by subtracting A from the universal set U, i.e., A C = U – A.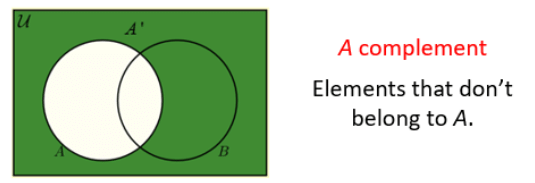
Example: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {2, 4, 6, 8}. Find AC
Ans: AC = U - A = {1, 3, 5, 7, 9, 10}
(V) Cartesian Product of Sets
The Cartesian product of two sets A and B, denoted as A × B, is the set of all ordered pairs (a, b) where a is an element of set A and b is an element of set B. This can be expressed in set-builder notation as:
A × B = {(a, b) : a ∈ A and b ∈ B}
Example: Set A = {1,2,3} and set B = {Bat, Ball}, then;
A × B = {(1,Bat),(1,Ball),(2,Bat),(2,Ball),(3,Bat),(3,Ball)}

Laws of Sets
(1) De Morgan's Laws: De Morgan's Laws describe the relationship between the union and intersection of sets and their complements. These laws can be stated as:
- (A U B)' = A' ∩ B'
- (A ∩ B)' = A' U B'
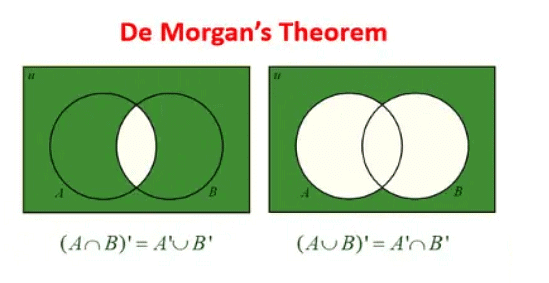
De Morgan's Laws can also be expressed in terms of set differences as:
- A - (B U C) = (A - B) ∩ (A - C)
- A - (B ∩ C) = (A - B) U (A - C)
(2) Complement Laws: The union of a set A and its complement A’ gives the universal set U of which, A and A’ are a subset.
A ∪ A’ = U
Also, the intersection of a set A and its complement A’ gives the empty set ∅.
A ∩ A’ = ∅
For Example: If U = {1 , 2 , 3 , 4 , 5 } and A = {1 , 2 , 3 } then A’ = {4 , 5}. From this it can be seen that
A ∪ A’ = U = { 1 , 2 , 3 , 4 , 5}
Also
A ∩ A’ = ∅
(3) Law of Double Complementation: According to this law if we take the complement of the complemented set A’ then, we get the set A itself.
(A’)’ = A
In the previous example we can see that, if U = {1 , 2 , 3 , 4 , 5} and A = {1 , 2 ,3} then A’ ={4 , 5}. Now if we take the complement of set ‘A’ we get,
(A’)’ = {1 , 2 , 3} = A
This gives back the set A itself.
(4) Law of empty set and universal set: The law of the empty set and universal set states that the complement of the universal set is the empty set, and vice versa. This can be expressed as: ∅' = U and U' = ∅
Example: If U = {a, b, c, d, e, f}, A = {a, b, c}, B = {c, d, e, f}, C = {c, d, e}, find (A ∩ B) ∪ (A ∩ C).
Ans: A ∩ B = {a, b, c} ∩ {c, d, e, f}
A ∩ B = { c }
A ∩ C = { a, b, c } ∩ { c, d, e }
A ∩ C = { c }
Then (A ∩ B) ∪ (A ∩ C) = { c }
Example: Give examples of finite sets.
Ans: The examples of finite sets are: Set of months in a year
- Set of days in a week
- The Set of natural numbers less than 20
- Set of integers greater than -2 and less than 3
Example: If U = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11}, A = {3, 5, 7, 9, 11} and B = {7, 8, 9, 10, 11}, Then find (A – B)′.
Ans: A – B is a set of member which belong to A but do not belong to B
∴ A – B = {3, 5, 7, 9, 11} – {7, 8, 9, 10, 11}
A – B = {3, 5}
According to formula, (A − B)′ = U – (A – B)
∴ (A − B)′ = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11} – {3, 5}
So, (A − B)′ = {2, 4, 6, 7, 8, 9, 10, 11}.
EduRev Tip: Any set is a subset of itself, but not a proper subset. The empty set, denoted by ∅ , is also a subset of any given set X. The empty set is always a proper subset, except of itself. Every other set is then a subset of the universal set.
|
205 videos|264 docs|136 tests
|
FAQs on Important Formulae: Set Theory - CSAT Preparation - UPSC
| 1. What are the different types of sets in set theory? |  |
| 2. How are sets represented in set theory? |  |
| 3. What are some common operations performed on sets in set theory? |  |
| 4. What are the laws of sets in set theory? |  |
| 5. What are some important formulae in set theory for CAT exam preparation? |  |
















