CAT Exam > CAT Notes > Quantitative Aptitude (Quant) > Important Formulas: HCF & LCM
Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |
|
| Meaning and Basics |
|
| Prime Factorisation Method |
|
| Short-cut Method |
|
| Relationship Between HCF and LCM |
|
| Important Results and Formulas |
|
| Shortcut Tricks |
|
| Solved Examples |
|
| Summary Table |
|
Meaning and Basics
- HCF (Highest Common Factor): The greatest number that divides two or more numbers exactly.
- Also called GCD (Greatest Common Divisor).
- LCM (Least Common Multiple): The smallest number that is exactly divisible by two or more numbers.
Prime Factorisation Method
Let two numbers be expressed as:
a = p₁ˣ¹ × p₂ˣ² × p₃ˣ³ × …
b = p₁ʸ¹ × p₂ʸ² × p₃ʸ³ × …
Then,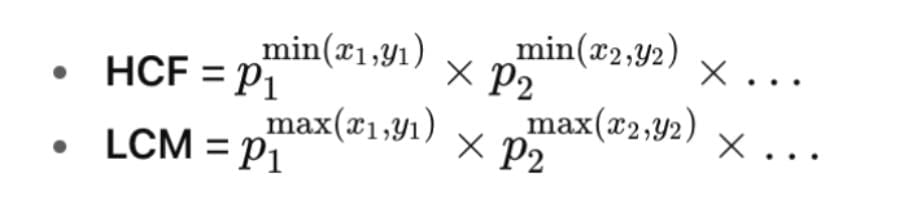
For finding HCF → take lowest powers of common primes.
For finding LCM → take highest powers of all primes.
Short-cut Method
(i) Using Division Method for HCF:
- Divide the larger number by the smaller one.
- Replace the larger number with the remainder.
- Continue dividing until the remainder = 0.
- The last non-zero remainder is the HCF.
(ii) Using Product Formula for LCM:
Once HCF is known, use: LCM = (Product of numbers) ÷ HCF.
Relationship Between HCF and LCM
- For two numbers a and b:
HCF × LCM = a × b - For three numbers a, b, and c:
HCF × LCM = (a × b × c) ÷ (HCF of pairwise combinations) - LCM of fractions = LCM of Numerators / HCF of Denominators
- HCF of fractions = HCF of Numerators / LCM of Denominators
Important Results and Formulas
| Concept | Formula / Explanation |
|---|---|
| Relation between two numbers | HCF × LCM = Product of the numbers |
| Relation between three numbers (co-prime) | HCF × LCM = Product of the numbers |
| When HCF and one number are given | LCM = (Product of numbers) ÷ HCF |
| When LCM and one number are given | HCF = (Product of numbers) ÷ LCM |
| HCF of fractions | HCF = HCF of Numerators ÷ LCM of Denominators |
| LCM of fractions | LCM = LCM of Numerators ÷ HCF of Denominators |
| If two numbers are co-prime | HCF = 1, hence LCM = Product of numbers |
| Ratio of two numbers | Ratio = a : b = HCF × (p : q), where p, q are co-prime |
| HCF of perfect squares/cubes | Always a perfect square/cube, respectively |
| Product of HCF and LCM of fractions | = Product of the given fractions |
Shortcut Tricks
1. When numbers are small:
- List their multiples/divisors manually.
- Pick the smallest common multiple → LCM.
- Pick the greatest common divisor → HCF.
2. When numbers are large:
Use Prime Factorisation or the Division Method.
3. If LCM and one number are known:
Other number = (HCF × LCM) ÷ Given number
Solved Examples
Example 1: Find the HCF and LCM of 12 and 18.
Sol:
Prime factors:
12 = 2² × 3¹
18 = 2¹ × 3²HCF = 2¹ × 3¹ = 6
LCM = 2² × 3² = 36Verification:
HCF × LCM = 6 × 36 = 216 = 12 × 18
Example 2: Find the LCM and HCF of fractions 3/4, 5/8, 7/12.
Sol:
HCF = (HCF of 3, 5, 7) ÷ (LCM of 4, 8, 12) = 1 ÷ 24 = 1/24
LCM = (LCM of 3, 5, 7) ÷ (HCF of 4, 8, 12) = 105 ÷ 4 = 105/4
Summary Table
| Topic | Formula / Concept |
|---|---|
| HCF × LCM = Product of two numbers | Always true |
| For three co-prime numbers | The same formula holds |
| HCF of fractions | HCF of numerators ÷ LCM of denominators |
| LCM of fractions | LCM of numerators ÷ HCF of denominators |
| HCF of decimals | Convert to integers and proceed normally |
| LCM of decimals | Convert to integers, find LCM, then divide by the appropriate power of 10 |
EduRev Tip: Always check divisibility and verify using the HCF–LCM product rule.
The document Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT is a part of the CAT Course Quantitative Aptitude (Quant).
All you need of CAT at this link: CAT
|
167 videos|238 docs|95 tests
|
FAQs on Important Formulas: HCF & LCM - Quantitative Aptitude (Quant) - CAT
| 1. What is the Prime Factorisation Method and how is it used to find HCF and LCM? |  |
Ans. The Prime Factorisation Method involves breaking down numbers into their prime factors. To find the HCF (Highest Common Factor), you identify the common prime factors and multiply them together. For LCM (Lowest Common Multiple), you take all the prime factors, each raised to the highest power that appears in the factorization of any of the numbers. This method provides a systematic way to determine both HCF and LCM.
| 2. Can you explain the relationship between HCF and LCM? | |
Ans. The relationship between HCF and LCM of two numbers can be expressed with the formula: HCF × LCM = Product of the two numbers. This means that if you know the HCF and one of the numbers, you can easily find the LCM by rearranging the formula. This relationship helps in simplifying many problems related to HCF and LCM.
| 3. What are some important results and formulas related to HCF and LCM? | |
Ans. Some important results and formulas include:
- HCF of a and b = Product of the common prime factors
- LCM of a and b = Product of all prime factors, each raised to the highest power
- For three numbers a, b, and c: HCF(a, b, c) = HCF(HCF(a, b), c) and LCM(a, b, c) = LCM(LCM(a, b), c). These results are crucial for solving problems involving multiple numbers.
| 4. What are some shortcut tricks for calculating HCF and LCM? | |
Ans. Some shortcut tricks include:
- For two numbers, if one is a multiple of the other, the HCF is the smaller number and the LCM is the larger number.
- For small numbers, you can often use the listing method to quickly find the HCF and LCM by listing the factors or multiples.
- Using the prime factorization method can also be expedited by memorizing the prime numbers and their products for common small numbers.
| 5. Can you provide an example of how to solve HCF and LCM problems? | |
Ans. For example, to find the HCF and LCM of 12 and 18:
- Prime factorization: 12 = 2² × 3¹; 18 = 2¹ × 3².
- HCF = 2¹ × 3¹ = 6.
- LCM = 2² × 3² = 36.
Therefore, the HCF of 12 and 18 is 6, and the LCM is 36.
About this Document
Oct 19, 2025
Last updated
Document Description: Important Formulas: HCF & LCM for CAT 2025 is part of Quantitative Aptitude (Quant) preparation.
The notes and questions for Important Formulas: HCF & LCM have been prepared according to the CAT exam syllabus. Information about Important Formulas: HCF & LCM covers topics
like Meaning and Basics, Prime Factorisation Method, Short-cut Method, Relationship Between HCF and LCM, Important Results and Formulas, Shortcut Tricks, Solved Examples, Summary Table and Important Formulas: HCF & LCM Example, for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulas: HCF & LCM.
Introduction of Important Formulas: HCF & LCM in English is available as part of our Quantitative Aptitude (Quant)
for CAT & Important Formulas: HCF & LCM in Hindi for Quantitative Aptitude (Quant) course.
Download more important topics related with notes, lectures and mock test series for CAT
Exam by signing up for free. CAT: Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT
Description
Full syllabus notes, lecture & questions for Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT - CAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude (Quant) | Best notes, free PDF download
Information about Important Formulas: HCF & LCM
In this doc you can find the meaning of Important Formulas: HCF & LCM defined & explained in the simplest way possible. Besides explaining types of
Important Formulas: HCF & LCM theory, EduRev gives you an ample number of questions to practice Important Formulas: HCF & LCM tests, examples and also practice CAT
tests
Related Searches
ppt
,practice quizzes
,Free
,Exam
,MCQs
,Objective type Questions
,study material
,mock tests for examination
,Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT
,Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT
,Important Formulas: HCF & LCM | Quantitative Aptitude (Quant) - CAT
,Extra Questions
,Sample Paper
,Important questions
,video lectures
,shortcuts and tricks
,Summary
,Viva Questions
,Semester Notes
,past year papers
,Previous Year Questions with Solutions
;
Additional Information about Important Formulas: HCF & LCM for CAT Preparation
Important Formulas: HCF & LCM Free PDF Download
The Important Formulas: HCF & LCM is an invaluable resource that delves deep into the core of the CAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulas: HCF & LCM now and kickstart your journey towards success in the CAT exam.
Importance of Important Formulas: HCF & LCM
The importance of Important Formulas: HCF & LCM cannot be overstated, especially for CAT aspirants.
This document holds the key to success in the CAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulas: HCF & LCM Notes
Important Formulas: HCF & LCM Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulas: HCF & LCM.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulas: HCF & LCM Notes on EduRev are your ultimate resource for success.
Important Formulas: HCF & LCM CAT Questions
The "Important Formulas: HCF & LCM CAT Questions" guide is a valuable resource for all aspiring students preparing for the
CAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulas: HCF & LCM on the App
Students of CAT can study Important Formulas: HCF & LCM alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulas: HCF & LCM,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulas: HCF & LCM is prepared as per the latest CAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily