Important Formulas: HCF & LCM | General Test Preparation for CUET - CUET Commerce PDF Download

The HCF and LCM of a given set of numbers can be calculated using different methods like the division method and the prime factorization method. HCF refers to the Highest Common Factor (HCF) of two or more given numbers and it is the largest number that divides each of the given numbers without leaving any remainder. The Least Common Multiple (LCM) of two or more numbers is the smallest of the common multiples of those numbers. It is important to learn HCF and LCM in mathematics as it helps us to solve our day-to-day problems related to grouping and sharing. Let us learn about the different methods used to find the HCF and LCM of numbers. 

What is HCF and LCM?

HCF is defined as the highest common factor present in two or more given numbers. It is also termed as the 'Greatest Common Divisor' (GCD). For example, the HCF of 24 and 36 is 12, because 12 is the largest number which can divide both the numbers completely. Similarly, the Least Common Multiple (LCM) of two or more numbers is the smallest number which is a common multiple of the given numbers. For example, let us take two numbers 8 and 16. The multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, and so on. The multiples of 16 are 16, 32, 48, 64, 80, 96, and so on. The first common value among these multiples is the Least Common Multiple (LCM) for 8 and 16, which is 16. Now, let us learn how to find the HCF and LCM of numbers.

How to Find HCF and LCM?

There are various methods that are used to find the Highest Common Factor (HCF) and Least Common Multiple (LCM) of numbers. The most common methods are:

• Prime factorization method
• Division method

Finding HCF and LCM by Prime Factorization

By using the prime factorization method for finding LCM and HCF, we first need to find the prime factors of the given numbers. Then, we can calculate the values of HCF and LCM by following the process explained below.

HCF by Prime Factorization
In order to find the HCF of the given numbers by prime factorization, we find the prime factors of those numbers. After finding the factors, we find the product of the prime factors that are common to each of the given numbers. In some cases, we multiply the common prime factors that have the least or smallest power to obtain the HCF of those numbers. For example, let us find the HCF of 50 and 75 by the prime factorization method.

• The prime factors of 50 = 2 × 5 × 5 or 2 × 5²
• The prime factors of 75 = 3 × 5 × 5 or 3 × 5²

The common factors of 50 and 75 are 5² or 5 × 5. Thus, HCF of (50, 75) = 25.

LCM by Prime Factorization

To calculate the LCM of any given set of numbers using the prime factorization method, we follow the steps given below:

• Step 1: List the prime factors of the given numbers.
• Step 2: After finding the prime factors, we write them in their exponent form, and then find the product of only those prime factors that have the highest power. The product of these factors with the highest powers is the LCM of the given numbers.

Example 1: Let us find the LCM of 160 and 90 using prime factorization.

• Step 1: The prime factors of 160 = 2 × 2 × 2 × 2 × 2 × 5. After writing this in the exponent form, we get 2⁵ × 5 and 90 = 2 × 3 × 3 × 5 or 2 × 3² × 5.
• Step 2: Now, if we pick the factors with the highest power, we get 2⁵, 3², and 5. The product of all these prime factors = 2⁵ × 3² × 5 = 1440.

Therefore, LCM of 160 and 90 = 1440.

Example 2: Find the LCM of 30 and 60 using prime factorization.
Sol: Let us find the LCM of 30 and 60 using the prime factorization method.

• Step 1: The prime factorization of 30 and 60 are: 30 = 2 × 3 × 5; and 60 = 2 × 2 × 3 × 5
• Step 2: If we write these prime factors in their exponent form it will be expressed as, 30 = 2¹ × 3¹ × 5¹ and 60 = 2² × 3¹ × 5¹
• Step 3: Now, we will find the product of only those factors that have the highest powers among these. This will be, 2² × 3¹ × 5¹ = 4 × 3 × 5 = 60

Therefore, the LCM of 30 and 60 is 60.

Finding HCF and LCM by Division Method

There are two different ways to apply the division method to find LCM and HCF. Let us learn it one by one.

HCF by Division Method
To find the HCF by division method, follow the steps given below.

• Step 1: First, we need to divide the larger number by the smaller number and check the remainder.
• Step 2: Make the remainder of the above step as the divisor and the divisor of the above step as the dividend and perform the division again.
• Step 3: Continue the division process till the remainder is not equal to 0.
• Step 4: The last divisor will be the HCF of the given numbers.

Let us understand this method using an example.
Example: Find the HCF of 198 and 360 using the division method.
Sol: Read out the following steps and relate them with the figure given below.

• Step 1: Divide 360 by 198. The obtained remainder is 162.
• Step 2: Make 162 as the divisor and 198 as the dividend and perform the division again. Here the obtained remainder is 36.
• Step 3: Make 36 as the divisor and 162 as the dividend and perform the division again. Here the obtained remainder is 18.
• Step 4: Make 18 as the divisor and 36 as the dividend and perform the division again. Here the obtained remainder is 0.
• Step 5: The last divisor, 18, is the HCF of 360 and 198.

LCM by Division Method

To find the LCM of numbers by the division method, we divide the numbers with prime numbers and stop the division process when we get only 1 in the final row. Observe the steps given below to find the LCM of the given numbers using the division method. Let us understand the method with the help of an example.

Example: Find the LCM of 7, 8, 14, and 21.
Sol:

• Step 1: Divide the numbers by the smallest prime number such that the prime number should at least divide 1 of the given numbers. Here, we will divide the numbers 7, 8, 14, 21 by the smallest prime number, i.e., 2.
• Step 2: Write the quotients of the divisible numbers right below the numbers in the next row and copy the other numbers as it is. So, the next row will be written in this way: 7, 4, 7, and 21.
• Step 3: Now, for the next division step consider the above quotients as the new dividends. Repeat the process and write the quotient below the numbers. Here, on dividing 7, 4, 7, 21 by 2, we get the quotients as 7, 2, 7, 21. [Only 4 was divisible by 2 in this step, so we copy the other three numbers as it is in the next row]
• Step 4: Repeat the steps and divide the new dividends till we get 1.
• Step 5: Multiply all the prime numbers on the left-hand side of the bar to get the LCM of the given numbers. This will be 2 × 2 × 2 × 3 × 7 = 168. Therefore, the LCM of 7, 8, 14 and 21 is 168.

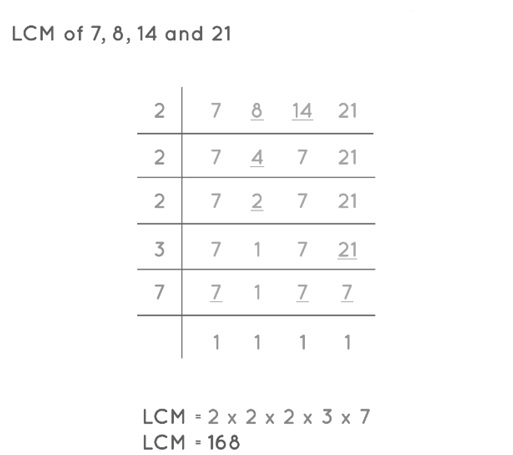
Therefore, the LCM of 7, 8, 14, and 21 is 168.
Let us learn more about the HCF and LCM formula in the following section.

HCF and LCM Formula

The LCM and HCF of two numbers share a relationship with each other. This is expressed in the form of a formula. The HCF and LCM formula of two numbers 'a' and 'b' is expressed as
HCF (a, b) × LCM (a, b) = a × b
In other words, the formula of HCF and LCM states that the product of any two numbers is equal to the product of their HCF and LCM. To know more about LCM and HCF relationship, visit this page which describes the relation between HCF and LCM.
The HCF and LCM formula is used in many ways. For example, if any one of the values of HCF or LCM is not known, we can easily find the other without using any of the methods given in the above sections. Let us understand this using an example.

Example: The HCF and LCM of 2 numbers is 8 and 96 respectively. If one of the two numbers is 24, find the other number.
Sol: HCF of the numbers = 8; LCM of the 2 numbers = 96; One number = 24, Second number = ?
Using the HCF and LCM formula, we can find the unknown value.
HCF (a, b) × LCM (a, b) = a × b
After substituting the values we get, 8 × 96 = 24 × b
So the value of 'b' = 768/24 = 32. Therefore, the other number is 32.

HCF and LCM Tricks

• If 1 is the HCF of 2 numbers, then their LCM will be their product. For example, the HCF of 2 and 3 is 1, now the LCM of 2 and 3 will be 2 × 3 = 6.
• For two coprime numbers, the HCF is always 1. For example, let us take two co-prime numbers 4 and 5, we can see that their HCF is 1 because co-prime numbers do not have any common factor other than 1.