Important Formulas: Hyperbola | Mathematics (Maths) for JEE Main & Advanced PDF Download

Hyperbola

The Hyperbola is a conic whose eccentricity is greater than unity. (e > 1).
1. Standard Equation & Definition(S)
Standard equation of the hyperbola is 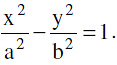Where b²= a² (e² − 1)or a² e² = a² + b² i.e. e2 = 1 +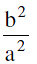 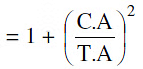FOCI :
S ≡ (ae, 0) & S' º (− ae, 0).
Equations of Directrices :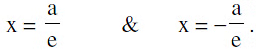

Vertices :
A ≡ (a, 0)& A' º (− a, 0). l (Latus rectum) = 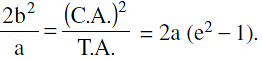Note : l (L.R.) = 2e (distance from focus to the corresponding directrix)
Transverse Axis :
The line segment A'A of length 2a in which the foci S' & S both lie is called the
T.A. of The Hyperbola.
Conjugate Axis :
The line segment B'B between the two points B' ≡ (0, − b) & B ≡ (0, b) is called as the
C.A. of The Hyperbola.
The T.A. & the C.A. of the hyperbola are together called the Principal axes of the hyperbola.

2. Focal Property :
The difference of the focal distances of any point on the hyperbola is constant and equal to transverse axis i.e. PS − PS' = 2a . The distance SS' = focal length.

3. Conjugate Hyperbola :
Two hyperbolas such that transverse & conjugate axes of one hyperbola are respectively the conjugate & the transverse axes of the other are called Conjugate Hyperbolas of each other.
eg. 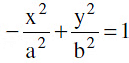are conjugate hyperbolas of each.Note :
(a) If e₁& e₂ are the eccentrcities of the hyperbola & its conjugate then e₁ ⁻² + e₂

⁻² = 1.
(b) The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.
(c) Two hyperbolas are said to be similiar if they have the same eccentricity.

4. Rectangular Or Equilateral Hyperbola :
The particular kind of hyperbola in which the lengths of the transverse & conjugate axis are equal is called an Equilateral Hyperbola. Note that the eccentricity of the rectangular hyperbola is 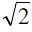and the length of its latus rectum is equal to its transverse or conjugate axis.

5. Auxiliary Circle :
A circle drawn with centre C & T.A. as a diameter is called the AUXILIARY CIRCLE of the hyperbola. Equation of the auxiliary circle is x² + y² = a².
Note from the figure that P & Q are called the "Corresponding Points " on the hyperbola & the auxiliary circle. 'θ' is called the eccentric angle of the point 'P' on the hyperbola. (0 ≤ θ < 2π).
Note : The equations x = a sec θ & y = b tan θ together represents the hyperbola where θ is a parameter. The parametric equations : x = a cos Ф,y = b sin h Ф also represents the same hyperbola.General Note :
Since the fundamental equation to the hyperbola only differs from that to the ellipse in having – b² instead of b² it will be found that many propositions for the hyperbola are derived from those for the ellipse by simply changing the sign of b².

6. Position Of A Point 'P' W.R.T. A Hyperbola :
The quantity 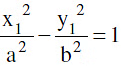is positive, zero or negative according as the point (x₁, y₁) lies within, upon or without the curve.
7. Line And A Hyperbola :
The straight line y = mx + c is a secant, a tangent or passes outside the hyperbola 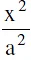+ 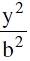= according as: c² > = < a² m² − b².

8. Tangents And Normals :
Tangents :
(a) Equation of the tangent to the hyperbola 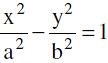at the point (x₁, y₁) is 

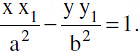Note: In general two tangents can be drawn from an external point (x₁ y₁) to the hyperbola and they are y − y₁ = m₁(x − x1) & y − y₁ = m₂(x − x₂), where m₁ & m₂ are roots of the equation (x₁² − a²)m² − 2 x₁y₁m + y₁² + b² = 0. If D < 0, then no tangent can be drawn from (x₁ y₁) to the hyperbola.
(b) Equation of the tangent to the hyperbola 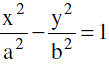at the point (a sec θ, b tan θ) is 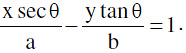Note : Point of intersection of the tangents at θ₁ & θ₂ is x = a 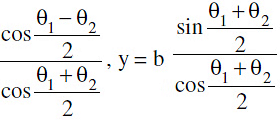(c) y = mx 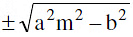can be taken as the tangent to the hyperbola 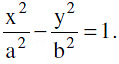Note that there are two parallel tangents having the same slope m.(d) Equation of a chord joining α & β is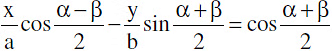 

Normals:
(a) The equation of the normal to the hyperbola 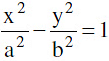at the point P(x₁, y₁) on it is 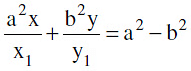= a² e².
(b) The equation of the normal at the point P (a secθ, b tanθ) on the hyperbola 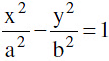is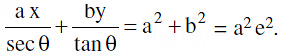(c) Equation to the chord of contact, polar, chord with a given middle point, pair of tangents from an external point is to be interpreted as in ellipse.

9. Director Circle :
The locus of the intersection of tangents which are at right angles is known as the Director Circle of the hyperbola. The equation to the director circle is : x² + y² = a² − b².
If b² < a² this circle is real; if b² = a² the radius of the circle is zero & it reduces to a point circle at the origin.
In this case the centre is the only point from which the tangents at right angles can be drawn to the curve. If b² > a², the radius of the circle is imaginary, so that there is no such circle & so no tangents at right angle can be drawn to the curve.

10. Highlights On Tangent And Normal :
H−1 Locus of the feet of the perpendicular drawn from focus of the hyperbola 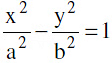upon any tangent is its auxiliary circle i.e. x² + y² = a² & the product of the feet of these perpendiculars is b2 · (semi C ·A)²
H−2 The portion of the tangent between the point of contact & the directrix subtends a right angle at the corresponding focus.
H−3 The tangent & normal at any point of a hyperbola bisect the angle between the focal radii. This spells the reflection property of the hyperbola as "An incoming light ray " aimed towards one focus is reflected from the outer surface of the hyperbola towards the other focus. It follows that if an ellipse and a hyperbola have the same foci, they cut at right angles at any of their common point.
Note that the ellipse 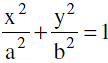and the hyperbola 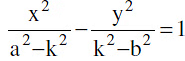(a > k > b > 0) Xare confocal and therefore orthogonal.H−4 The foci of the hyperbola and the points P and Q in which any tangent meets the tangents at the vertices are concyclic with PQ as diameter of the circle.

11. Asymptotes:
Definition :
If the length of the perpendicular let fall from a point on a hyperbola to a straight line tends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called the Asymptote of the Hyperbola.
To find the asymptote of the hyperbola :
Let y = mx + c is the asymptote of the hyperbola 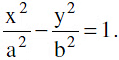Solving these two we get the quadratic as(b²− a²m²) x²− 2a² mcx − a2 (b² + c²) = 0 ....(1)
In order that y = mx + c be an asymptote, both roots of equation (1) must approach infinity, the conditions for which are :
coeff of x² = 0 & coeff of x = 0.
⇒ b² − a²m² = 0 or m = 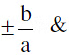a² mc = 0 ⇒ c = 0.
∴ equations of asymptote are 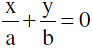and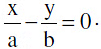combined equation to the asymptotes 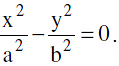Particular Case :
When b = a the asymptotes of the rectangular hyperbola. x² − y² = a² are, y = ± x which are at right angles.
Note :
(i) Equilateral hyperbola ⇔ rectangular hyperbola.
(ii) If a hyperbola is equilateral then the conjugate hyperbola is also equilateral.
(iii) A hyperbola and its conjugate have the same asymptote.
(iv) The equation of the pair of asymptotes differ the hyperbola & the conjugate hyperbola by the same constant only.
(v) The asymptotes pass through the centre of the hyperbola & the bisectors of the angles between the asymptotes are the axes of the hyperbola.
(vi) The asymptotes of a hyperbola are the diagonals of the rectangle formed by the lines drawn through the extremities of each axis parallel to the other axis.
(vii) Asymptotes are the tangent to the hyperbola from the centre.
(viii) A simple method to find the coordinates of the centre of the hyperbola expressed as
a general equation of degree 2 should be remembered as:
Let f (x, y) = 0 represents a hyperbola.
Find 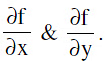Then the point of intersection of  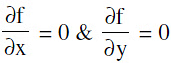gives the centre of the hyperbola.

12. Highlights On Asymptotes:
H−1 If from any point on the asymptote a straight line be drawn perpendicular to the transverse axis, the product of the segments of this line, intercepted between the point & the curve is always equal to the square of the semi conjugate axis.
H−2 Perpendicular from the foci on either asymptote meet it in the same points as the corresponding directrix & the common points of intersection lie on the auxiliary circle.
H−3 The tangent at any point P on a hyperbola 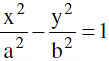with centre C, meets the asymptotes in Q and R and cuts off a Δ CQR of constant area equal to ab from the asymptotes & the portion of the tangent intercepted between the asymptote is bisected at the point of contact. This implies that locus of the centre of the circle circumscribing the Δ CQR in case of a rectangular hyperbola is the hyperbola itself & for a standard hyperbola the locus would be the curve, 4(a²x² − b²y²) = (a² + b²)².
H−4 If the angle between the asymptote of a hyperbola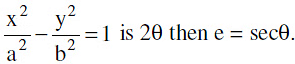

13. Rectangular Hyperbola : Rectangular hyperbola referred to its asymptotesas axis of coordinates.
(a) Eq. is xy = c² with parametric representation x = ct, y = c/t, t ∈ R – {0}.
(b) Eq.of a chord joining the points (t₁) & (t₂) is x + t₁t₂y = c(t₁ + t₂) with slope m =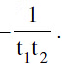 

(c) Equation of the tangent at P (x₁, y₁) is 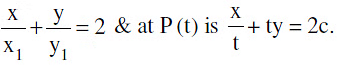(d) Equation of normal : 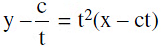(e) Chord with a given middle point as (h, k) is kx + hy = 2hk.