Important Formulas: Linear Equations in One Variable | Mathematics (Maths) Class 8 PDF Download
Algebraic Equation
An algebraic equation is an equality involving variables. It says that the value of the expression on one side of the equality sign is equal to the value of the expression on the other side.
Examples:
- Expressions: 5x, 2x - 3, x2 + 1, y + y2, etc.
- Equations: 5x = 25, 2x - 3 = 9, 6z + 10 = -2, etc.
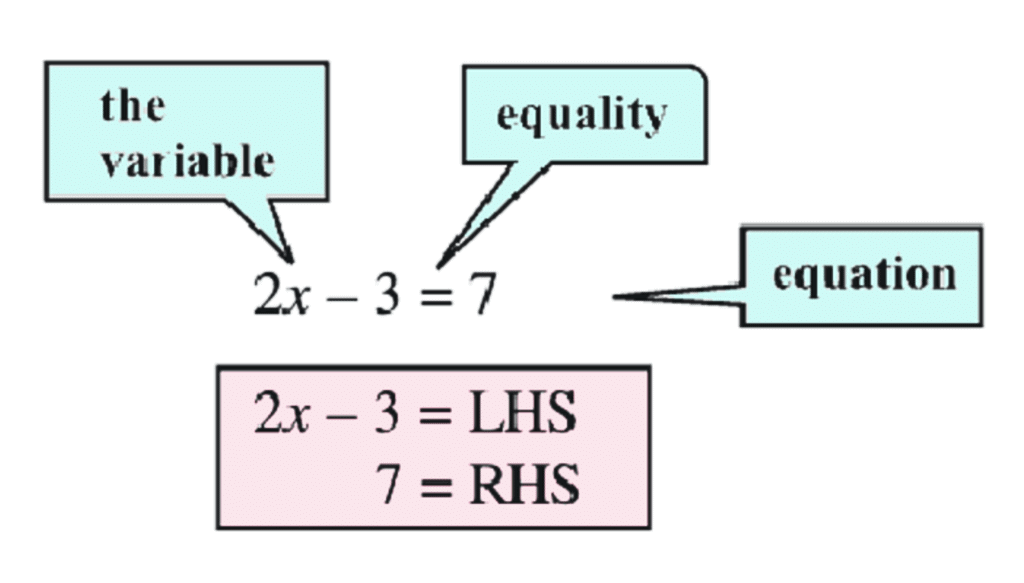
What is Linear equation in one Variable
- A linear equation is where the highest power of the variable is 1.
- These equations typically have one variable and are straightforward to solve.
- Examples: 2x, 3y - 7, 12 - 5z.
Non-Linear Expressions:
- Expressions with higher powers of variables (e.g., x2 + 1, y3 + y ) are not linear equations.

Important points to Note
- These all equation contains the equality (=) sign.
- The expression on the left of the equality sign is the Left Hand Side (LHS). The expression on the right of the equality sign is the Right Hand Side (RHS).
- In an equation the values of the expressions on the LHS and RHS are equal. This happens to be true only for certain values of the variable. These values are the solutions of the equation.
- We assume that the two sides of the equation are balanced. We perform the same mathematical operations on both sides of the equation, so that the balance is not disturbed. We get the solution after generally performing few steps.
- A linear equation in one variable has only one solution.
How to solve Linear equation in one variable
Type of method
1. Solving Equations which have Linear Expressions on one Side and Numbers on the other Side
Working of method
- Transpose (changing the side of the number) the Numbers to the side where all number are present. We know the sign of the number changes when we transpose it to other side.
- Now you will have an equation have variable on one side and number on other side. Add/subtract on both the side to get single term.
- Now divide or multiply on both the side to get the value of the variable.
Example : Solve 2x - 3 = 7
Sol: Add 3 to both sides:
2x = 7 + 3
2x = 10
Now, transpose 2 to RHS and solve for x:
x = 102
x = 5
2. Solving Equations having the Variable on both Sides
Working of method
- Here we Transpose (changing the side of the number) both the variable and Numbers to the side so that one side contains only the number and other side contains only the variable. We know the sign of the number changes when we transpose it to other side. Same is the case with Variable.
- Now you will have an equation have variable on one side and number on other side. Add/subtract on both the side to get single term.
- Now divide or multiply on both the side to get the value of the variable.
Example: Solve 3x - 4 = 2x + 6
Sol: We have
3x - 4 = 2x + 6. _____[ transposing 2x to LHS and -4 to RHS]
we get ,
3x - 2x = 6 + 4
solving the algebric equation we get,
x = 10
3. Solving Complex Equations (having number in denominator) having the Variable on both Sides
Working of method
- Take the LCM of the denominator of both the LHS and RHS.
- Multiple the LCM on both the sides, this will reduce the number without denominator and we can solve using the method described above.
Example : Solve
4x + 52 + 2 = x - 24
Sol: Multiply both sides by 4:
4 × 4x + 52 + 4 × 2 = 4 × x - 24
On simplifying equation we get ,
2(4x + 5) + 8 = x - 2
8x + 10 + 8 = x - 2
8x + 18 = x - 2
transposing x to LHS and 18 to RHS, we get,
8x - x = -2 - 18
7x = -20
transposing 7 to RHS, we get
x = -207
Thus, the required solution is x = -207.
4. Equations Reducible to the Linear Form
Working of method
- Here the equation is of the form
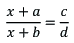
- We can cross multiply the numerator and denominator to reduce it to linear for (x+a)d=c(x+b) Now it can be solved by above method.
Example : Solve:
2x - 47 = x + 64
Sol: Cross-multiply:
4(2x - 4) = 7(x + 6)
Expand both sides:
8x - 16 = 7x + 42
Move terms involving x to one side and constants to the other:
8x - 7x = 42 + 16
x = 58
|
81 videos|423 docs|31 tests
|
FAQs on Important Formulas: Linear Equations in One Variable - Mathematics (Maths) Class 8
| 1. What is a linear equation in one variable? |  |
| 2. How can we solve a linear equation in one variable? |  |
| 3. What are some examples of linear equations in one variable? |  |
| 4. What is the importance of the solution to a linear equation in one variable? |  |
| 5. How do we check if our solution to a linear equation is correct? |  |






















