SAT Exam > SAT Notes > Mathematics for Digital SAT > Important Formulas: Linear Equations in One Variable
Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT PDF Download
| Table of contents |
|
| Algebraic Equation |
|
| What is Linear Equation in One Variable |
|
| Important Formulas |
|
| Important Points to Note |
|
| How to Solve Linear Equation in One Variable |
|
Algebraic Equation
- An algebraic equation is an equality involving variables.
- It says that the value of the expression on one side of the equality sign is equal to the value of the expression on the other side.
What is Linear Equation in One Variable
- Linear equations in one variable is an algebraic equation of equality that involves only one variable, the greatest exponent of which is 1.
- There is a single root or solution for every linear equation in one variable.
- This root or solution is a value that when replaced with the variable makes the equation true.
Example: Consider the linear equation in one variable: 4x+6=14
Can you tell what is the number that should replace ‘x’ so that the given equation results in a true statement?
The linear equation will result in a true statement when the value of ‘x’ is 2.
4∗2+6=8+6=14
The linear equation will not result in a true statement if the value of ‘x’ is taken other than 2. Thus, the given equation 4x + 6 = 14 results in a true statement only when ‘x’ is replaced by 2. In this case, we call the number 2, the root or the solution of equation 4x + 6 = 14.
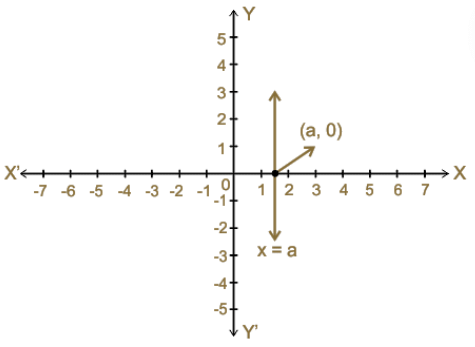Graph: Linear Equation in One Variable
Standard form of linear equations in one variable is written as ax+b=0, (a is not equal to zero) where x is the one variable while a and b are any real numbers.
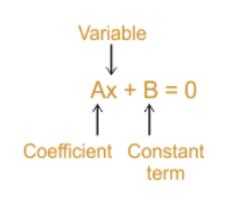
Important Formulas
Important Points to Note
- All equations contain the equality (=) sign.
- The expression on the left of the equality sign is the Left Hand Side (LHS). The expression on the right of the equality sign is the Right Hand Side (RHS).
- In an equation, the values of the expressions on the LHS and RHS are equal. This happens to be true only for certain values of the variable. These values are the solutions of the equation.
- We assume that the two sides of the equation are balanced. We perform the same mathematical operations on both sides of the equation, so that the balance is not disturbed. We get the solution after generally performing few steps.
- A linear equation in one variable has only one solution.
How to Solve Linear Equation in One Variable
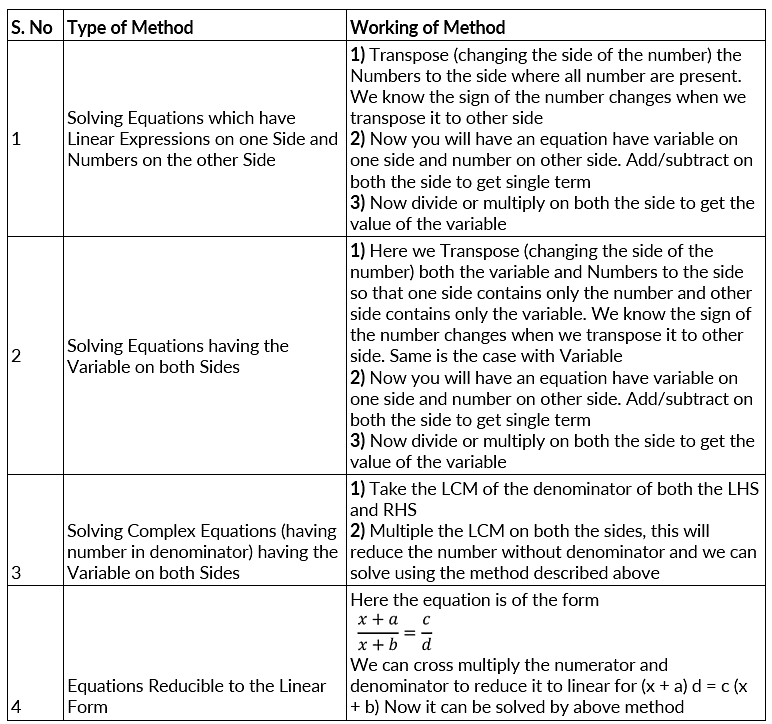
Rules to Solve
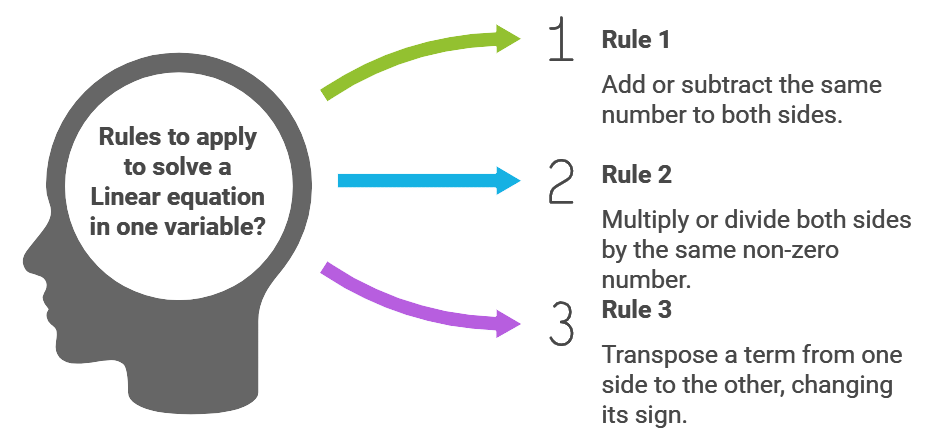
Rule 1: Adding the same number (positive or negative) to both sides of an equation, then the resulting equation will be equivalent to the original equation.
Rule 2: Multiplying or dividing both sides of an equation by the same non-zero number, then the resulting equation will be equivalent to the original equation.
Rule 3: Transposing a term from one side to the other side of the equation, then the resulting equation will be equivalent to the original equation, but remember that the sign of the transposed term changes.
The document Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT is a part of the SAT Course Mathematics for Digital SAT.
All you need of SAT at this link: SAT
|
185 videos|124 docs|75 tests
|
FAQs on Important Formulas: Linear Equations in One Variable - Mathematics for Digital SAT
| 1. What is a linear equation in one variable? |  |
Ans. A linear equation in one variable is an algebraic expression that can be written in the form \( ax + b = 0 \), where \( a \) and \( b \) are constants, and \( x \) is the variable. The equation represents a straight line when graphed, hence the term "linear."
| 2. How do you solve a linear equation in one variable? | |
Ans. To solve a linear equation in one variable, follow these steps:
1. Simplify both sides of the equation, if necessary.
2. Isolate the variable \( x \) on one side by performing inverse operations (addition, subtraction, multiplication, or division) on both sides of the equation.
3. Solve for \( x \) to find its value.
| 3. What are some important formulas related to linear equations in one variable? | |
Ans. Important formulas include:
- Standard form: \( ax + b = 0 \)
- Slope-intercept form: \( y = mx + c \) (not applicable directly to one variable but useful in understanding linear relationships)
- Solution formula: If \( ax + b = 0 \), then \( x = -\frac{b}{a} \).
| 4. What are the important points to note when solving linear equations in one variable? | |
Ans. Important points to note include:
- Ensure the equation is simplified correctly.
- Remember to perform the same operation on both sides to maintain equality.
- Be cautious of operations that can change the sign of a variable, such as multiplying or dividing by a negative number.
| 5. Can a linear equation in one variable have more than one solution? | |
Ans. No, a linear equation in one variable has exactly one solution unless it is an identity (true for all values of the variable) or a contradiction (no possible solutions). For example, \( 2x + 4 = 0 \) has one solution, while \( 2x + 4 = 2x + 4 \) is an identity and has infinitely many solutions.
About this Document
|
4.70/5 Rating |
|
Nov 22, 2024 Last updated |
Document Description: Important Formulas: Linear Equations in One Variable for SAT 2024 is part of Mathematics for Digital SAT preparation.
The notes and questions for Important Formulas: Linear Equations in One Variable have been prepared according to the SAT exam syllabus. Information about Important Formulas: Linear Equations in One Variable covers topics
like Algebraic Equation, What is Linear Equation in One Variable, Important Formulas, Important Points to Note, How to Solve Linear Equation in One Variable and Important Formulas: Linear Equations in One Variable Example, for SAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulas: Linear Equations in One Variable.
Introduction of Important Formulas: Linear Equations in One Variable in English is available as part of our Mathematics for Digital SAT
for SAT & Important Formulas: Linear Equations in One Variable in Hindi for Mathematics for Digital SAT course.
Download more important topics related with notes, lectures and mock test series for SAT
Exam by signing up for free. SAT: Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT
Description
Full syllabus notes, lecture & questions for Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT - SAT | Plus excerises question with solution to help you revise complete syllabus for Mathematics for Digital SAT | Best notes, free PDF download
Information about Important Formulas: Linear Equations in One Variable
In this doc you can find the meaning of Important Formulas: Linear Equations in One Variable defined & explained in the simplest way possible. Besides explaining types of
Important Formulas: Linear Equations in One Variable theory, EduRev gives you an ample number of questions to practice Important Formulas: Linear Equations in One Variable tests, examples and also practice SAT
tests
|
Explore Courses for SAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT
,Previous Year Questions with Solutions
,Exam
,practice quizzes
,mock tests for examination
,video lectures
,Sample Paper
,Objective type Questions
,ppt
,Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT
,MCQs
,Viva Questions
,past year papers
,Important Formulas: Linear Equations in One Variable | Mathematics for Digital SAT
,Semester Notes
,Extra Questions
,Free
,Important questions
,Summary
,shortcuts and tricks
,study material
;
Additional Information about Important Formulas: Linear Equations in One Variable for SAT Preparation
Important Formulas: Linear Equations in One Variable Free PDF Download
The Important Formulas: Linear Equations in One Variable is an invaluable resource that delves deep into the core of the SAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulas: Linear Equations in One Variable now and kickstart your journey towards success in the SAT exam.
Importance of Important Formulas: Linear Equations in One Variable
The importance of Important Formulas: Linear Equations in One Variable cannot be overstated, especially for SAT aspirants.
This document holds the key to success in the SAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulas: Linear Equations in One Variable Notes
Important Formulas: Linear Equations in One Variable Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulas: Linear Equations in One Variable.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulas: Linear Equations in One Variable Notes on EduRev are your ultimate resource for success.
Important Formulas: Linear Equations in One Variable SAT Questions
The "Important Formulas: Linear Equations in One Variable SAT Questions" guide is a valuable resource for all aspiring students preparing for the
SAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulas: Linear Equations in One Variable on the App
Students of SAT can study Important Formulas: Linear Equations in One Variable alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulas: Linear Equations in One Variable,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulas: Linear Equations in One Variable is prepared as per the latest SAT syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup