Important Formulas: Power Play | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| 1. Exponential Notation |

|
| 2. Laws of Exponents |

|
| 3. Scientific Notation |

|
| 4. Prime Factorization in Exponential Form |

|
| 5. Combinations |

|
| 6. Linear vs. Exponential Growth |

|
1. Exponential Notation
Formula: A number n multiplied by itself a times is expressed as: nᵃ
Example:
2 × 2 × 2 × 2 = 2⁴ = 16
2. Laws of Exponents
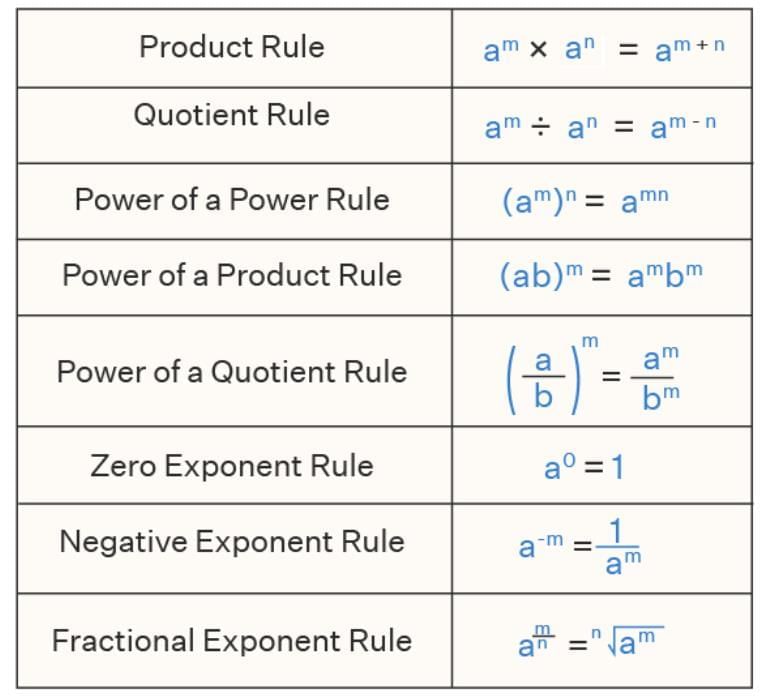 Here are the laws of exponents when a and b are non-zero integers and m, n are any integers.
Here are the laws of exponents when a and b are non-zero integers and m, n are any integers.
a. Product Rule
Formula:
nᵃ × nᵇ = nᵃ⁺ᵇ
Example:
2³ × 2⁴ = 2³⁺⁴ = 2⁷ = 128
b. Power of a Power Rule
Formula:
(nᵃ)ᵇ = nᵃ×ᵇ = (nᵇ)ᵃ
Example:
(2³)² = 2³×² = 2⁶ = 64
c. Quotient Rule
Formula:
nᵃ ÷ nᵇ = nᵃ⁻ᵇ
Example:
2⁵ ÷ 2² = 2⁵⁻² = 2³ = 8
d. Product of Different Bases
Formula:
nᵃ × mᵃ = (n × m)ᵃ
Example:
2³ × 3³ = (2 × 3)³ = 6³ = 216
e. Zero Exponent Rule
Formula:
n⁰ = 1 (n ≠ 0)
Example:
5⁰ = 1
f. Negative Exponent Rule
Formula:
n⁻ᵃ = 1/nᵃ
Example:
2⁻³ = 1/2³ = 1/8

3. Scientific Notation
Formula: A number is written as:
x × 10ᵃ where 1 ≤ x < 10, a is an integer
Example:
Number: 59,853
Scientific notation:
59,853 = 5.9853 × 10⁴
4. Prime Factorization in Exponential Form
Formula: Express a number as a product of prime factors in exponential form.
Example:
Number: 32,400
Prime factorization:
32,400 = 2⁴ × 3⁴ × 5²
5. Combinations
Formula: For k items, each with n choices, the total number of combinations is: nᵏ
Example:
A 5-digit password using digits 0–9:
10⁵ = 100,000 combinations
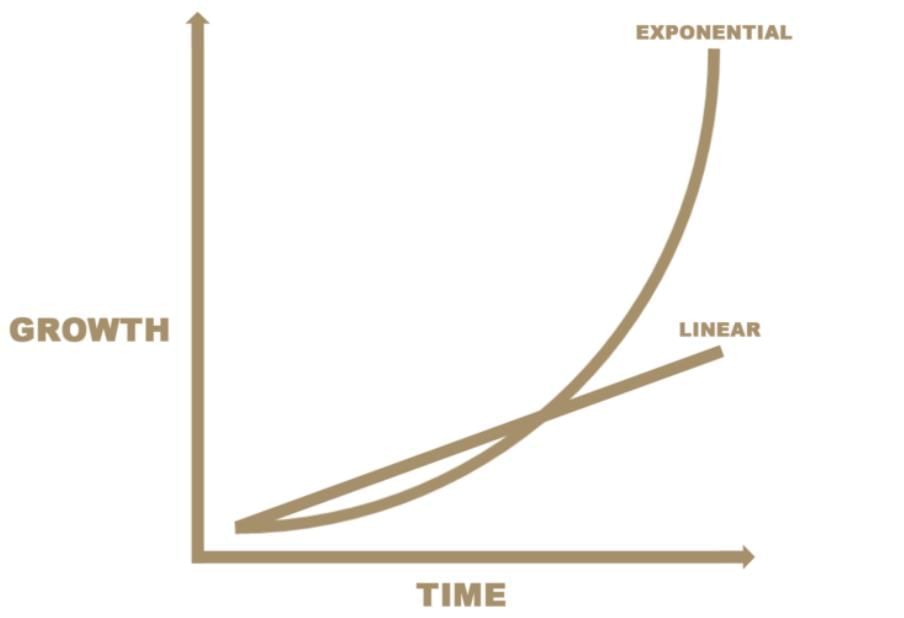
6. Linear vs. Exponential Growth
a. Linear Growth
Description: Adds a fixed amount per step.
Example:
Distance to the Moon: 384,400 km = 384,400,000 m
Step size: 20 cm = 0.2 m
Number of steps:
384,400,000 / 0.2 = 1,922,000,000 steps = 1.922 × 10⁹
b. Exponential Growth
Description: Multiplies by a fixed factor per step.
Example: Paper folding to the Moon:
Initial thickness: 0.001 cm
Number of folds: 46
Thickness:
T = 0.001 × 2⁴⁶ ≈ 7,036,874,841,600 cm ≈ 703,687.48 km
|
26 videos|133 docs|11 tests
|
FAQs on Important Formulas: Power Play - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the significance of the Power Play concept in Class 8 mathematics? |  |
| 2. How do you calculate the value of a number raised to a power? |  |
| 3. Can you provide examples of real-life applications of exponents? |  |
| 4. What are some common mistakes students make when dealing with powers and exponents? |  |
| 5. How can students practice and improve their understanding of powers and exponents? |  |
















