Important Formulas: Quadratic Equations | Quantitative Aptitude for SSC CGL PDF Download

Definition of Quadratic Equation

A quadratic equation is a form of polynomial equation in a single variable, typically denoted as "x," and can be presented in the standard form: ax² + bx + c = 0. In this representation, "a," "b," and "c" are constants, with the condition that "a" must not equal 0.

Clear all your SSC CGL doubts with EduRev Join for Free

Join for Free

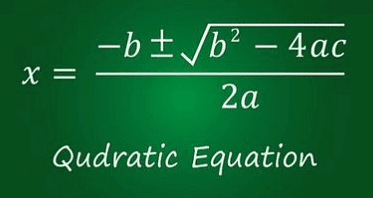
Formula for Quadratic Equation & Definitions

• An equation where the highest exponent of the variable is a square. Standard form of quadratic equation is ax²+bx+c = 0
• Where,  x is the unknown variable and a, b, c are the numerical coefficients.

Quadratic Equations Formulas

• If ax²+bx+c = 0 is a quadratic equation, then the value of x is given by the following formula
• 

MCQ: Quadratic Equations - 1

Start Test

Start Test

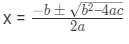
Formula of Quadratic Equation & Method of Quadratic Questions

1. Factorization 

It is very simple method to to solve quadratic equations. Factorization give 2 linear equations

For example:  x² + 3x – 4 = 0
Here, a = 1, b = 3 and c = -4
Now, find two numbers whose product is – 4 and sum is 3.
So, the numbers are 4 and -1.
Therefore, two factors will be 4 and -1

2. Completing the Square Method

Every Quadratic question has always a square term. If we could get two square terms of quality sign we can get a linear equations. Middle term is called as ‘b’ and splited by (b/2)² 
For exampl : – x²+ 4x +4
Here x² =1, b= 4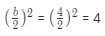

(x+2)² = 3
Take the square of both side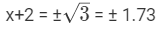

Therefore, x = -0.27 or -3.73

Formulas of Quadratic Equations & Key points to Remember

Other basic concepts to remember while solving quadratic equations are:

1.Nature of roots

• Nature of roots determine whether the given roots of the equation are real, imaginary, rational or irrational. The basic formula is b² – 4ac.
• This formula is also called discriminant or D. The nature of the roots depends on the value of D. Conditions to determine the nature of the roots are:
• If D < 0, than the given roots are imaginary.
• If D = 0, then roots given are real and equal.
• If D > 0, then roots are real and unequal.
• Also, in case of D > 0, if the equation is a perfect square than the given roots are rational, or else they are irrational.

2. Sum and product of the roots

• For any given equation the sum of the roots will always be 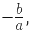 and the product of the roots will be  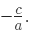 Thus, the standard quadratic equation can also be written as x² – (Α + Β)x + Α*Β = 0

3. Forming a quadratic equation

• The equation can be formed when the roots of the equation are given or the product and sum of the roots are given.

Questions on Quadratic Equations

Q1: Which of the following is the general form of a quadratic equation?
(a) x² + 3x – 2 = 0
(b) 3x + 2 = 5
(c) 2x – 4 = 0
(d) 5x² – 7x = 3
Ans: (a)
The general form of a quadratic equation is ax² + bx + c = 0, where “a,” “b,” and “c” are constants. Option A follows this format, representing a quadratic equation.

Q2: Which method is most suitable for solving the quadratic equation x² – 6x + 9 = 0?
(a) Factoring
(b) Quadratic Formula
(c) Completing the Square
(d) Graphical Analysis
Ans: (c)
The quadratic equation x² – 6x + 9 = 0 is a perfect square trinomial, and completing the square is the most efficient method to solve it. This method involves transforming the equation into a squared binomial, which makes it easy to find the solutions.

Q3: Which of the following quadratic equations has complex roots?
(a) 2x² + 4x + 5 = 0
(b) x² + 6x + 9 = 0
(c) 3x² – 6x + 3 = 0
(d) 5x² – 10x + 5 = 0
Ans: (a)
The discriminant (Δ) of a quadratic equation determines the nature of its roots. If Δ < 0, the equation has complex roots. For option A, the discriminant is 4² – 4(2)(5) = 16 – 40 = -24, which is negative. Therefore, the quadratic equation 2x² + 4x + 5 = 0 has complex roots.

Q4: What is the discriminant of the quadratic equation 2x² – 5x + 3 = 0?
(a) 1
(b) -11
(c) -19
(d) 11
Ans: (c)
The discriminant (Δ) of a quadratic equation ax² + bx + c = 0 is given by the expression Δ = b² – 4ac. Substituting the coefficients from the given equation, we have Δ = (-5)² – 4(2)(3) = 25 – 24 = 1. Therefore, the discriminant is 1.

Q5: For the quadratic equation 2x² + 5x – 3 = 0, what are the roots?
(a) x = -3 and x = 1/2
(b) x = 3 and x = -1/2
(c) x = -3 and x = -1/2
(d) x = 3 and x = 1/2
Ans: (a)
The quadratic equation can be factored as (2x – 3)(x + 1) = 0. Setting each factor equal to zero gives 2x – 3 = 0 and x + 1 = 0. Solving for “x” in each equation yields x = 3/2 and x = -1. Therefore, the roots are x = -3 and x = 1/2.