SSC CGL Exam > SSC CGL Notes > Quantitative Aptitude for SSC CGL > Important Formulas: Quadrilateral and Polygons
Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL PDF Download
Quadrilateral Types
Example of Quadrilateral:
Q: If the area of a rectangle is 48 and the length is 8, what is the width?
Sol: Given, area=48, and l=8
To find: width w
Formula: l×w
Area of rectangle=l×w
48 = 8(w)
w=48 / 8 = 6
Polygon
In the realm of Mathematics, a polygon is identified as a two-dimensional closed figure, composed of straight line segments. It's worth noting that a polygon is not a three-dimensional shape and does not contain any curved surfaces. A polygon must have at least three sides, and each line segment should intersect with another line segment only at its endpoint. The shape of a polygon can be easily recognized from the number of sides it possesses. Below is a list of various polygon shapes along with their corresponding number of sides.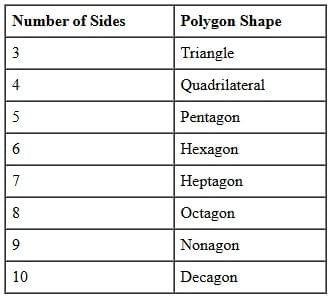
Classification of Polygons:
Polygons can be classified based on their angle measurements and the length of their sides. Here are the main types:
- Regular Polygon – All sides and interior angles are of equal measurement
- Irregular Polygon – The sides and interior angles vary in measurement
- Convex polygon – All the interior angles of a polygon are strictly less than 180 degrees
- Concave Polygon – At least one interior angle of a polygon exceeds 180 degrees
Formulas Related to Polygons:
Here are some important formulas related to polygons:
- The sum of interior angles of a polygon with “n” sides =180°(n-2)
- Number of diagonals in an “n-sided” polygon = [n(n-3)]/2
- The measure of interior angles in a regular n-sided polygon = [(n-2)180°]/n
- The measure of exterior angles in a regular n-sided polygon = 360°/n
Key Properties of Polygons:
Here are some important properties of polygons:
- The sum of all interior angles in a quadrangle equals 360 degrees.
- A polygon is termed as concave if at least one of its interior angles is greater than 180 degrees.
- A polygon is termed as a simple polygon if it does not cross over itself and has only one boundary. If not, it is a complex polygon.
Example of a Polygon
Q: Calculate the sum of the interior angles of a pentagon.
Sol:
We know that a pentagon has five sides.
The formula to calculate the sum of interior angles is:
Sum of interior angles = 180°(n-2)
= 180°(5-2)
= 180° (3)
= 540°
Therefore, the sum of the interior angles of a pentagon equals 540°.
The document Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL is a part of the SSC CGL Course Quantitative Aptitude for SSC CGL.
All you need of SSC CGL at this link: SSC CGL
|
317 videos|290 docs|185 tests
|
FAQs on Important Formulas: Quadrilateral and Polygons - Quantitative Aptitude for SSC CGL
| 1. What are the different types of quadrilaterals based on their properties? |  |
Ans. Quadrilaterals can be classified into several types based on their properties:
1. <b>Parallelogram</b>: Opposite sides are parallel and equal in length.
2. <b>Rectangle</b>: A parallelogram with four right angles.
3. <b>Rhombus</b>: A parallelogram with all sides equal in length.
4. <b>Square</b>: A rectangle with all sides equal.
5. <b>Trapezium (or Trapezoid)</b>: At least one pair of opposite sides is parallel.
6. <b>Kite</b>: Two pairs of adjacent sides are equal in length.
| 2. What are the important formulas related to quadrilaterals? | |
Ans. Some key formulas related to quadrilaterals include:
1. <b>Area of a rectangle</b>: A = length × width.
2. <b>Area of a square</b>: A = side².
3. <b>Area of a parallelogram</b>: A = base × height.
4. <b>Area of a trapezium</b>: A = ½ × (sum of parallel sides) × height.
5. <b>Area of a rhombus</b>: A = (diagonal₁ × diagonal₂) / 2.
| 3. How can one determine if a quadrilateral is a parallelogram? | |
Ans. A quadrilateral can be determined to be a parallelogram if any of the following conditions are met:
1. Opposite sides are equal in length.
2. Opposite angles are equal.
3. The diagonals bisect each other.
4. One pair of opposite sides is both equal and parallel.
| 4. What is the significance of the sum of the interior angles in a quadrilateral? | |
Ans. The sum of the interior angles of a quadrilateral is always 360 degrees. This property is crucial for solving various geometric problems, as it helps in determining unknown angles when some are provided. This rule applies to all types of quadrilaterals.
| 5. How can the area of a quadrilateral be calculated if the lengths of all sides are known? | |
Ans. If the lengths of all sides of a quadrilateral are known, one can use Brahmagupta's formula for cyclic quadrilaterals, which states:
Area = √[s(s-a)(s-b)(s-c)(s-d)], where s = (a+b+c+d)/2 and a, b, c, d are the lengths of the sides. If the quadrilateral is not cyclic, the area can also be found using triangulation or other methods like the coordinate geometry approach.
About this Document
Oct 06, 2025
Last updated
Related Exams
Document Description: Important Formulas: Quadrilateral and Polygons for SSC CGL 2025 is part of Quantitative Aptitude for SSC CGL preparation.
The notes and questions for Important Formulas: Quadrilateral and Polygons have been prepared according to the SSC CGL exam syllabus. Information about Important Formulas: Quadrilateral and Polygons covers topics
like Quadrilateral Types, Polygon and Important Formulas: Quadrilateral and Polygons Example, for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulas: Quadrilateral and Polygons.
Introduction of Important Formulas: Quadrilateral and Polygons in English is available as part of our Quantitative Aptitude for SSC CGL
for SSC CGL & Important Formulas: Quadrilateral and Polygons in Hindi for Quantitative Aptitude for SSC CGL course.
Download more important topics related with notes, lectures and mock test series for SSC CGL
Exam by signing up for free. SSC CGL: Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL
Description
Full syllabus notes, lecture & questions for Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL - SSC CGL | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude for SSC CGL | Best notes, free PDF download
Information about Important Formulas: Quadrilateral and Polygons
In this doc you can find the meaning of Important Formulas: Quadrilateral and Polygons defined & explained in the simplest way possible. Besides explaining types of
Important Formulas: Quadrilateral and Polygons theory, EduRev gives you an ample number of questions to practice Important Formulas: Quadrilateral and Polygons tests, examples and also practice SSC CGL
tests
Related Searches
ppt
,MCQs
,mock tests for examination
,Previous Year Questions with Solutions
,past year papers
,practice quizzes
,Semester Notes
,Sample Paper
,Viva Questions
,study material
,Objective type Questions
,Important questions
,Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL
,Summary
,Exam
,Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL
,Extra Questions
,Free
,video lectures
,Important Formulas: Quadrilateral and Polygons | Quantitative Aptitude for SSC CGL
,shortcuts and tricks
;
Additional Information about Important Formulas: Quadrilateral and Polygons for SSC CGL Preparation
Important Formulas: Quadrilateral and Polygons Free PDF Download
The Important Formulas: Quadrilateral and Polygons is an invaluable resource that delves deep into the core of the SSC CGL exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulas: Quadrilateral and Polygons now and kickstart your journey towards success in the SSC CGL exam.
Importance of Important Formulas: Quadrilateral and Polygons
The importance of Important Formulas: Quadrilateral and Polygons cannot be overstated, especially for SSC CGL aspirants.
This document holds the key to success in the SSC CGL exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulas: Quadrilateral and Polygons Notes
Important Formulas: Quadrilateral and Polygons Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulas: Quadrilateral and Polygons.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulas: Quadrilateral and Polygons Notes on EduRev are your ultimate resource for success.
Important Formulas: Quadrilateral and Polygons SSC CGL Questions
The "Important Formulas: Quadrilateral and Polygons SSC CGL Questions" guide is a valuable resource for all aspiring students preparing for the
SSC CGL exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulas: Quadrilateral and Polygons on the App
Students of SSC CGL can study Important Formulas: Quadrilateral and Polygons alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulas: Quadrilateral and Polygons,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulas: Quadrilateral and Polygons is prepared as per the latest SSC CGL syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup