Important Vector Formulas for JEE and NEET
1. Definitions:
A Vector may be described as a quantity having both magnitude & direction. A vector is generally represented by a directed line segment, say 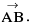 . A is called the initial point & B is called the terminal point. The magnitude of vector
. A is called the initial point & B is called the terminal point. The magnitude of vector 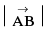 is expressed by
is expressed by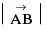 .
.
Zero vector a vector of zero magnitude i.e.which has the same initial & terminal point, is called a Zero vector. It is denoted by O.
Unit vector a vector of unit magnitude in direction of a vector 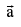 is called unit vector along
is called unit vector along 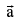 and is denoted by aˆ symbolically
and is denoted by aˆ symbolically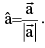
Equal vectors two vectors are said to be equal if they have the same magnitude, direction & represent the same physical quantity.
Collinear vectors two vectors are said to be collinear if their directed line segments are parallel disregards to their direction. Collinear vectors are also called Parallel vectors. If they have the same direction they are named as like vectors otherwise.
unlike vectors. Symbolically, two non zero vectors 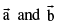 are collinear if and only if,
are collinear if and only if,
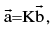 where K ∈ R Coplanar vectors a given number of vectors are called coplanar if their line segments are all parallel to the same plane. Note that “two vectors are always coplanar”. position vector let O be a fixed origin, then the position vector of a point P is the vector →OP . If a & b & position vectors of two point A and B, then , →AB = b a
where K ∈ R Coplanar vectors a given number of vectors are called coplanar if their line segments are all parallel to the same plane. Note that “two vectors are always coplanar”. position vector let O be a fixed origin, then the position vector of a point P is the vector →OP . If a & b & position vectors of two point A and B, then , →AB = b a
− = pv of B − pv of A .
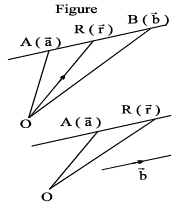
2. Vector addition:
If two vectors 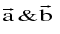 are represented by →
are represented by → 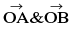 , then their sum
, then their sum 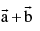 is a vector represented by
is a vector represented by 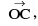 , where OC is the diagonal of the parallelogram OACB.
, where OC is the diagonal of the parallelogram OACB.
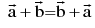 (commutative)
(commutative)
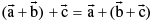 (associativity)
(associativity)
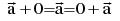
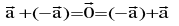
3. Multiplication of vector by scalars :
If 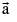 is a vector & m is a scalar, then m
is a vector & m is a scalar, then m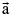 is a vector parallel to
is a vector parallel to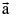 whose modulus is |m| times that of
whose modulus is |m| times that of 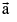 . This multiplication is called Scalar multiplication. If
. This multiplication is called Scalar multiplication. If 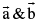 are vectors & m, n are scalars, then:
are vectors & m, n are scalars, then:
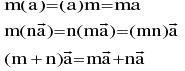
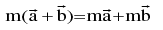
4. Section formula :
If 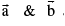 are the position vectors of two points A & B then the p.v. of a point which divides AB in the ratio m : n is given by :
are the position vectors of two points A & B then the p.v. of a point which divides AB in the ratio m : n is given by : 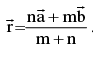
note p.v..of mid point of AB = 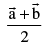
5. Direction Cosines
Let 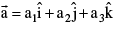 the angles which this vector makes with the +ve directions OX,OY & OZ are called Direction angles & their cosines are called the Direction cosines
the angles which this vector makes with the +ve directions OX,OY & OZ are called Direction angles & their cosines are called the Direction cosines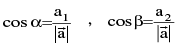
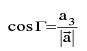 Note that, cos² αααα + cos² ββββ + cos² ΓΓΓΓ = 1.
Note that, cos² αααα + cos² ββββ + cos² ΓΓΓΓ = 1.
6. Vector equation of a line:
Parametric vector equation of a line passing through two point 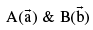
is given by,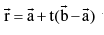 where t is a parameter. If the line passes through the point
where t is a parameter. If the line passes through the point 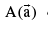 & is parallel to the vector then
& is parallel to the vector then 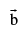 its equation is,
its equation is, 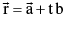
Note that the equations of the bisectors of the angles between the lines 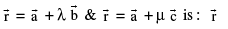

7. Test of collinearity :
Three points A,B,C with position vectors 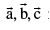
respectively are collinear, if & only if there exist scalars x , y , z not all zero simultaneously such that ; 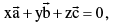 where x + y + z = 0.
where x + y + z = 0.
8. Scalar product of two vectors:
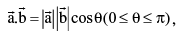 note that if θ is acute then
note that if θ is acute then 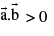 & if θ is obtuse then
& if θ is obtuse then 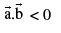
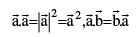 (commutative)
(commutative)
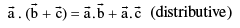
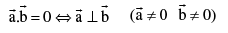
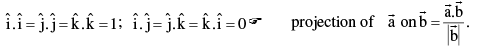
Note: That vector component of  and perpendicular to
and perpendicular to 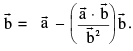 the angle φ between
the angle φ between 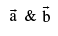 is given by cos φ =
is given by cos φ = 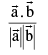 0 ≤ φ ≤ π.
0 ≤ φ ≤ π.
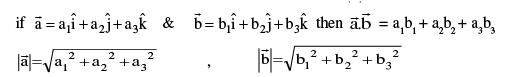
Note : (i) Maximum value of 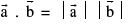
(ii) Minimum values of 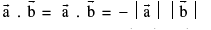
(iii) Any vector  can be written as
can be written as 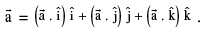
(iv) A vector in the direction of the bisector of the angle between the two vectors 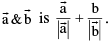 Hence bisector of the angle between the two vector
Hence bisector of the angle between the two vector 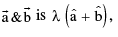 where
where 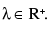 Bisector of the exterior angle between
Bisector of the exterior angle between 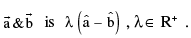
9. Vector product of two vectors :
(i) If 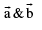 are two vectors & θ is the angle between them then
are two vectors & θ is the angle between them then 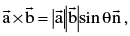 where
where 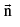 is the unit vector perpendicular to both
is the unit vector perpendicular to both 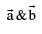 such that
such that  forms a right handed screw system.
forms a right handed screw system.
(ii) Lagranges Identity : for any two vectors 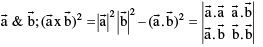
(iii) Formulation of vector product in terms of scalar product:
The vector product 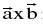 is the vector
is the vector 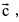 such that.
such that.
(i) 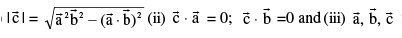 form a right handed system.
form a right handed system.
(iv) 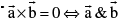 are parallel (collinear)
are parallel (collinear) 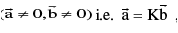 where K is a scalar..
where K is a scalar..

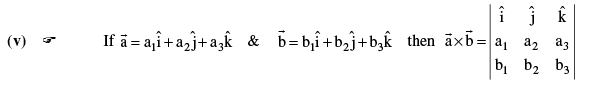
(vi) Geometrically 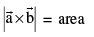 of the parallelogram whose two adjacent sides are represented by
of the parallelogram whose two adjacent sides are represented by 
(vii) Unit vector perpendicular to the plane of 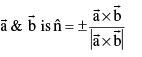
- A vector of magnitude ‘r ’ & perpendicular to the palne of 
If θ is the angle between 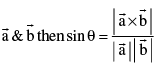
(viii) Vector area If 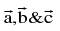 are the pv’s of 3 points A, B & C then the vector area of triangle ABC
are the pv’s of 3 points A, B & C then the vector area of triangle ABC 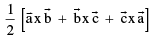 The points A, B & C are collinear if
The points A, B & C are collinear if 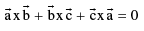
Area of any quadrilateral whose diagonal vectors are 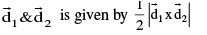
10. Shortest distance between two lines:
If two lines in space intersect at a point, then obviously the shortest distance between them is zero. Lines which do not intersect & are also not parallel are called SKEW LINES. For Skew lines the direction of the shortest distance would be perpendicular to both the lines. The magnitude of the shortest distance vector would be equal to that of the projection of  along the direction of the line of shortest distance,
along the direction of the line of shortest distance,  is parallel to
is parallel to 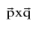 i. e .
i. e . 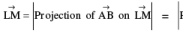
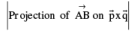
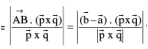
1. The two lines directed along 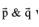 will intersect only if shortest distance = 0 i.e.
will intersect only if shortest distance = 0 i.e.
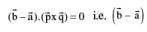 lies in the plane containing
lies in the plane containing 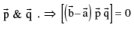
2. If two lines are given by 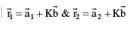 i.e. they are parallel then
i.e. they are parallel then 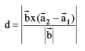
11. Scalar triple product / box product / mixed product :
The scalar triple product of three vectors  is defined as :
is defined as :
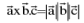 sin θ cos φ where θ is the angle between
sin θ cos φ where θ is the angle between 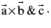 it is also defined as
it is also defined as 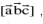 spelled as box product .Scalar triple product geometrically represents the volume of the parallelopiped whose three couterminous edges are represented by
spelled as box product .Scalar triple product geometrically represents the volume of the parallelopiped whose three couterminous edges are represented by 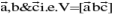
In a scalar triple product the position of dot & cross can be interchanged i.e.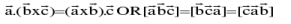
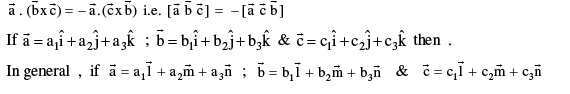
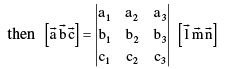 where
where 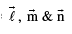 are non coplanar vectors .
are non coplanar vectors .
If 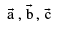 are coplanar
are coplanar 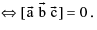
Scalar product of three vectors, two of which are equal or parallel is 0 i.e.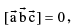
Note : If 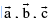 are non − coplanar then
are non − coplanar then 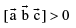 for right handed system &
for right handed system & 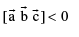 for left handed system .
for left handed system .
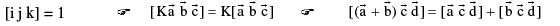
The volume of the tetrahedron OABC with O as origin & the pv’s of A, B and C being 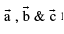 respectively is given by
respectively is given by 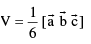
The positon vector of the centroid of a tetrahedron if the pv’s of its angular vertices are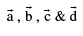 are given by
are given by 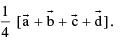
Note that this is also the point of concurrency of the lines joining the vertices to the centroids of the opposite faces and is also called the centre of the tetrahedron. In case the tetrahedron is regular it is equidistant from the vertices and the four faces of the tetrahedron .
12. Vector Triple Product : Let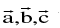 be any three vectors, then the expression
be any three vectors, then the expression  is a vector & is called a vector triple product .
is a vector & is called a vector triple product .
Geometrical interpretation of 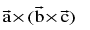
Consider the expression 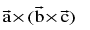 which itself is a vector, since it is a cross product of two vectors
which itself is a vector, since it is a cross product of two vectors 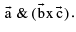 Now
Now  is a vector perpendicular to the plane containing
is a vector perpendicular to the plane containing 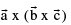 but
but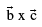 is a vector perpendicular to the plane
is a vector perpendicular to the plane 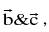 therefore
therefore 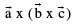 is a vector lies in the plane of
is a vector lies in the plane of 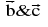 and perpendicular to
and perpendicular to 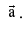 Hence we can express
Hence we can express 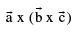 in terms of
in terms of 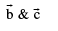 i.e.
i.e. 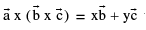 where x & y are scalars .
where x & y are scalars .
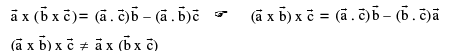
13. Linear combinations / Linearly Independence and Dependence of Vectors :
Given a finite set of vectors 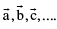 then the vector
then the vector 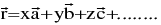
is called a linear combination of 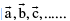 for any x, y, z ...... ∈ R. We have the following results :
for any x, y, z ...... ∈ R. We have the following results :
(a) Fundamental theorem in plane : Let 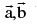 be non zero , non collinear vectors . Then any vector
be non zero , non collinear vectors . Then any vector 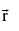 coplanar with
coplanar with 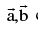 can be expressed uniquely as a linear combination of
can be expressed uniquely as a linear combination of 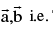 There exist some unique x,y ∈ R such that
There exist some unique x,y ∈ R such that 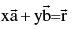
(b) Fundamental theorem in space : Let 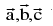 be non−zero, non−coplanar vectors in space. Then any vector
be non−zero, non−coplanar vectors in space. Then any vector 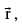 can be uniquily expressed as a linear combination of
can be uniquily expressed as a linear combination of 
There exist some unique x,y ∈ R such that 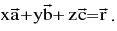
(c) If 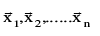 are n non zero vectors, & k1, k2, .....kn are n scalars & if the linear combination
are n non zero vectors, & k1, k2, .....kn are n scalars & if the linear combination 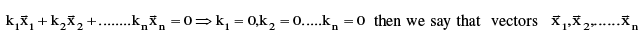
Linearly independent vectors
(d) If 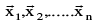 are not Linearly independent then they are said to be Linearly dependent vectors
are not Linearly independent then they are said to be Linearly dependent vectors 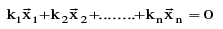 & if there exists at least one kr ≠ 0 then
& if there exists at least one kr ≠ 0 then
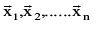 are said to be linearly dependent .
are said to be linearly dependent .
Note:
If 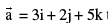 then
then 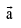 is expressed as a linear combination of vectors
is expressed as a linear combination of vectors  form a linearly dependent set of vectors. In general , every set of four vectors is a linearly dependent system.
form a linearly dependent set of vectors. In general , every set of four vectors is a linearly dependent system. 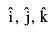 are Linearly independent set of vectors. For
are Linearly independent set of vectors. For 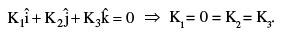
Two vectors 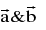 are linearly dependent ⇒
are linearly dependent ⇒ 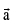 is parallel to
is parallel to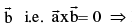 linear dependence of
linear dependence of 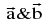 Conversely if
Conversely if 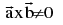 then
then 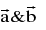 are linearly independent .
are linearly independent .
If three vectors 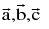 are linearly dependent, then they are coplanar i.e.
are linearly dependent, then they are coplanar i.e. 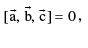
conversely, if 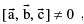 then the vectors are linearly independent.
then the vectors are linearly independent.
14. Coplanarity of vectors:
Four points A, B, C, D with position vectors 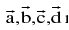 respectively are coplanar if and only if there exist scalars x, y, z, w not all zero simultaneously such that
respectively are coplanar if and only if there exist scalars x, y, z, w not all zero simultaneously such that 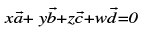 where, x + y + z + w = 0.
where, x + y + z + w = 0.
15. Reciprocal system of vectors:
If 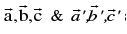 are two sets of non coplanar vectors such that
are two sets of non coplanar vectors such that 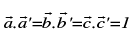
then the two systems are called Reciprocal System of vectors.
Note: 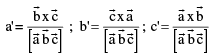
16. Equation of a plane
(a) The equation 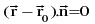 represents a plane containing the point with
represents a plane containing the point with
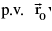 where
where 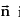 is a vector normal to the plane .
is a vector normal to the plane .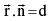 is the general equation of a plane.
is the general equation of a plane.
(b) Angle between the 2 planes is the angle between 2 normals drawn to the planes and the angle between a line and a plane is the compliment of the angle between the line and the normal to the plane.
17. Application of vectors:
(a) Work done against a constant force 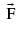 over a displacement
over a displacement 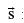 is defined as
is defined as
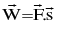
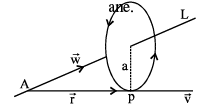
(b) The tangential velocity 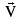 of a body moving in a circle is given by
of a body moving in a circle is given by 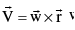 where
where 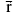 is the pv of the point P.
is the pv of the point P.
(c) The moment of 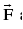 about ’O’ is defined as
about ’O’ is defined as 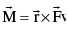 is the pv of P wrt ’O’. The direction of
is the pv of P wrt ’O’. The direction of 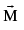 is along the normal to the plane OPN such that
is along the normal to the plane OPN such that 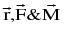
form a right handed system.
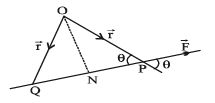
(d) Moment of the couple = 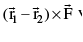 where
where 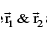 are pv’s of the point of the application of the forces
are pv’s of the point of the application of the forces 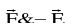 .
.
|
172 videos|503 docs|154 tests
|
















