HCF & LCM Important Notes | Quantitative Aptitude for Competitive Exams - SSC MTS / SSC GD PDF Download
| Table of contents |

|
| Introduction |

|
| What is H.C.F.? |

|
| What is L.C.M.? |

|
| H.C.F. and L.C.M. Formula |

|
| H.C.F. and L.C.M. Relation |

|
| How to Find L.C.M. and H.C.F.? |

|
Introduction
The full forms of H.C.F. and L.C.M. are Highest Common Factor and Least Common Multiple, respectively. H.C.F. refers to the largest factor shared between two or more numbers, while L.C.M. refers to the smallest number that is exactly divisible by two or more numbers. H.C.F. is also known as the Greatest Common Factor (GCF), and L.C.M. is sometimes referred to as the Least Common Divisor.
What is H.C.F.?
According to mathematical rules, the greatest common divisor (GCD) of two or more positive integers is the largest positive integer that divides all the numbers exactly, without leaving a remainder.
For example, consider the numbers 8 and 12.
The GCD (or H.C.F.) of 8 and 12 is 4, as 4 is the largest number that can divide both 8 and 12 evenly.
What is L.C.M.?
In arithmetic, the least common multiple (LCM) of two numbers, say a and b, is represented as LCM(a, b). The LCM is the smallest positive integer that is divisible by both a and b.
For example, consider the numbers 4 and 6.
Multiples of 4 are: 4, 8, 12, 16, 20, 24, and so on.
Multiples of 6 are: 6, 12, 18, 24, and so on.
The common multiples of 4 and 6 are 12, 24, 36, 48, etc., and the least common multiple among them is 12.
Now, let's find the LCM of 24 and 15: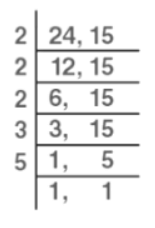 LCM of 24 and 15 = 2 × 2 × 2 × 3 × 5 = 120.
LCM of 24 and 15 = 2 × 2 × 2 × 3 × 5 = 120.
LCM of Two Numbers
Consider two numbers, 8 and 12, for which we need to find the LCM.
Let's list the multiples of these numbers:
Multiples of 8 are: 16, 24, 32, 40, 48, 56, and so on.
Multiples of 12 are: 24, 36, 48, 60, 72, 84, and so on.
As observed, the least common multiple, or the smallest common multiple, of 8 and 12 is 24.
H.C.F. and L.C.M. Formula
 The formula that involves both HCF and LCM is:
The formula that involves both HCF and LCM is:
Product of Two Numbers = (HCF of the two numbers) × (LCM of the two numbers)
For two numbers A and B, the formula can be written as:
A × B = HCF(A, B) × LCM(A, B)
This formula can also be expressed in terms of HCF and LCM as follows:
HCF of Two Numbers = (Product of Two Numbers) / LCM of Two Numbers
LCM of Two Numbers = (Product of Two Numbers) / HCF of Two Numbers.
H.C.F. and L.C.M. Relation
The following outlines the relationship between HCF and LCM. By understanding these relationships, you can solve problems more easily using the appropriate formulas.
(i) The product of the L.C.M. and H.C.F. of two given natural numbers is equal to the product of those numbers.
Based on this property,
LCM × HCF of two numbers = Product of the Numbers.
For two numbers A and B, this can be written as:
LCM(A, B) × HCF(A, B) = A × B.
Example: Show that the LCM (6, 15) × HCF (6, 15) = Product (6, 15)
Solution: LCM and HCF of 6 and 15:
6 = 2 × 3
15 = 3 x 5
LCM of 6 and 15 = 30
HCF of 6 and 15 = 3
LCM (6, 15) × HCF (6, 15) = 30 × 3 = 90
Product of 6 and 15 = 6 × 15 = 90
Hence, LCM (6, 15) × HCF (6, 15)=Product(6, 15) = 90
(ii) The L.C.M. of given co-prime numbers is equal to the product of those numbers, as the H.C.F. of co-prime numbers is 1.
Thus, LCM of co-prime numbers = Product of the numbers.
Example: 17 and 23 are two co-prime numbers. By using the given numbers verify that, LCM of given co-prime Numbers = Product of the given Numbers
Solution: LCM and HCF of 17 and 23:
17 = 1 x 7
23 = 1 x 23
LCM of 17 and 23 = 391
HCF of 17 and 23 = 1
Product of 17 and 23 = 17 × 23 = 391
Hence, LCM of co-prime numbers = Product of the numbers
(iii) H.C.F. and L.C.M. of Fractions.
LCM of fractions = LCM of Numerators / HCF of Denominators
HCF of fractions = HCF of Numerators / LCM of Denominators
Example 1: Find the LCM of the fractions 1/2 , 3/8, 3/4.
Solution: LCM of fractions = LCM of Numerators/HCF of Denominators
LCM of fractions = LCM (1,3,3)/HCF(2,8,4) = 3/2
Example 2: Find the HCF of the fractions 3/5, 6/11, 9/20.
Solution: HCF of fractions HCF of Numerators/LCM of Denominators
HCF of fractions = HCF (3,6,9)/LCM (5,11,20) = 3/220
How to Find L.C.M. and H.C.F.?
We can calculate the HCF and LCM of given natural numbers using two methods: the prime factorization method or the division method. In the prime factorization method, the given numbers are expressed as the product of prime factors. In the division method, the numbers are divided by the least common factor, and the process continues until the remainder is zero.
Note: Prime numbers are those that have only two factors: one and the number itself.
L.C.M. by Prime Factorization Method
In this method, the given natural numbers are expressed as the product of prime factors. The least common multiple (LCM) is then determined by taking the product of all prime factors raised to the highest power (degree).
Example: Find the LCM of 20 and 12 by prime factorization method.
Solution: Step 1: To find LCM of 20 and 12, write each number as a product of prime factors.
20 = 2 × 2 × 5 = 22 × 5
12 = 2 × 2 × 3 = 22 × 3
Step 2: Multiply all the prime factors with the highest degree.
Here we have 2 with highest power 2 and other prime factors 3 and 5. Multiply all these to get LCM.
LCM of 20 and 12 = 2 × 2 × 3 × 5 = 22 × 3 × 5 = 60
L.C.M. by Division Method
In this method, continuously divide the given numbers by a common prime number until the remainder is either a prime number or one. The LCM is then found by multiplying all the divisors and the remaining prime numbers.
Example: Find the LCM of 24 and 15 by the division method.
Solution: Step 1: Divide the given numbers by the least prime number.
Here, 2 is the least number which will divide 24.
Step 2: Write the quotient and the number which is not divisible by the above prime number in the second row.
In the second row, write the quotient we get after the division of 24 by 2. Since 15 is not divisible by 2, write 15 in the second row as it is.
Step 3: Divide the numbers with another least prime number.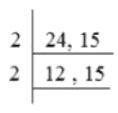 Step 4: Continue division until the remainder is a prime number or 1.
Step 4: Continue division until the remainder is a prime number or 1.
Step 5: Multiply all the divisors and remaining prime number (if any) to obtain the LCM.
LCM of 24 and 15 = 2 × 2 × 2 × 3 × 5 = 23 × 3 × 5 = 120
H.C.F. By Prime Factorization Method
To express given natural numbers as the product of their prime factors, find the highest common factor by multiplying all the common prime factors with the smallest exponent (power).
Example: Find the HCF of 20 and 12 by prime factorization method.
Solution: Step 1: To find HCF of 20 and 12, write each number as a product of prime factors.
20 = 2 × 2 × 5 = 22 × 5
12 = 2 × 2 × 3 = 22 × 3
Step 2: Multiply all the common prime factors with the lowest degree.
Here we have only 2 as a common prime factor with the lowest power of 2.
HCF of 20 and 12 = 22 = 4
H.C.F. by Division Method
In this method, keep dividing the largest number by the smallest number among the given numbers until the remainder becomes zero. The final divisor will be the HCF of the given numbers.
Example: Find the LCM of 24 and 15 by the division method.
Solution: Step 1: Divide the largest number by the smallest number.
Here, the largest number is 24 and the smaller one is 15. Divide 24 by 15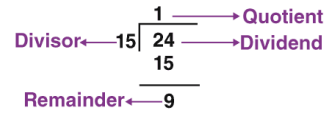
Step 2: Take divisor as new dividend and remainder as the new divisor, i.e. divide the first divisor by the first remainder.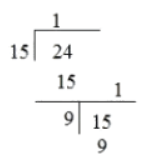 Step 3: Proceed till the remainder is zero and the last divisor will be the HCF of the given numbers.
Step 3: Proceed till the remainder is zero and the last divisor will be the HCF of the given numbers.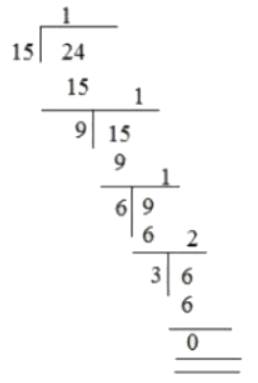
Therefore, HCF of 24 and 15 is 3.
Alternatively, we can divide both the numbers by the least common prime factor, still there is no more common prime factors. Multiply all divisors to get the HCF of given numbers.
Consider the above example, HCF of 24 and 15 can also be calculated using the following steps:
Step 1: Divide the given numbers by the least common prime factor.
Here, 3 is the least common prime factor of 24 and 15.
Step 2: Continue still there is no more common prime factor. Then multiply all the divisors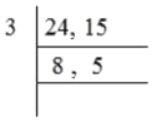 Division of 24 and 15 by 3 will leave 8 and 5 as their remainders respectively. 8 and 5 do not have a common prime factor.
Division of 24 and 15 by 3 will leave 8 and 5 as their remainders respectively. 8 and 5 do not have a common prime factor.
Hence, the HCF of 24 and 15 is 3.
|
203 videos|110 docs|114 tests
|















