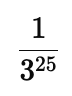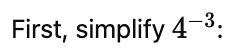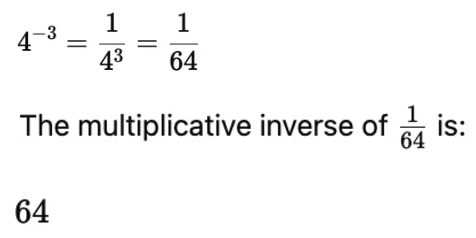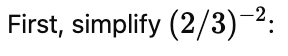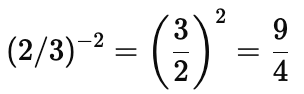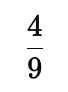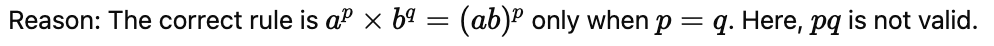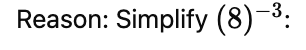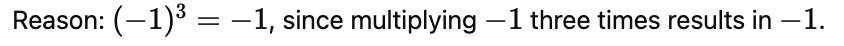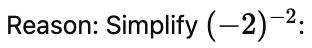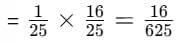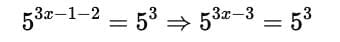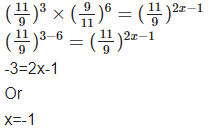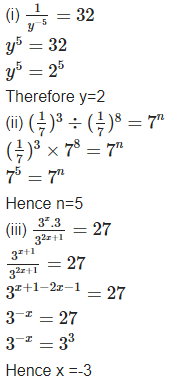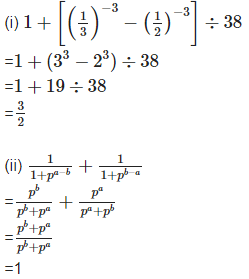Important Questions for Class 8 Maths - Exponents and Powers

Q1: Evaluate
(i) 2-2
(ii) (-2)-2
(iii) (3/2)-5
Sol:
As we know that
b-n= 1/bn
(i) 2-2 = 1/ 22 =1/4
(ii) (-2)-2 = 1/(-2)2 = 1/4
(iii) (3/2)-5 = 3-5/ 2-5 =25/35 = 32/243
Q2: Find the value of.
(i) (40 + 4-1) × 22
(ii) (3-1 × 9-1) ÷ 3-2
(iii)(11-1 + 12-1 + 13-1)0
Sol:
(i) (40 + 4-1) × 22 = (1+1/4) × 4 = 4 + 1 =5
(ii) (3-1 × 9-1) ÷ 3-2 = [(1/3) × (1/9)] ÷ (1/9) =1/3
(iii) (11-1 + 12-1 + 13-1)0 =1 as a0= 1
Q3: Find the value of m for which 2m ÷ 2-4 = 45
Sol:
2m ÷ 2-4 = 45
2m × (1/2-4) = 210
2m+4 =210
So m + 4 = 10
m = 6
Q4: Express the following numbers in usual form.
(i) 34.02 x 10-5
(ii) 9.5 x 105
(iii) 9 x 10-4
(iv) 2.0001 x 108
Sol:
(i) 34.02 x 10-5 = 0.0003402
(ii) 9.5 x 105 = 950000
(iii) 9 x 10-4 = 0.0009
(iv) 2.0001 x 108 =200010000
Q5: Find the Multiplicative inverse of
(i) 325
(ii) 4−3
(iii) (2/3)−2
Sol:
(i) The multiplicative inverse of a number is the number that, when multiplied by the original number, equals 1.
(ii) 4-3
(iii) (2/3)2
Q6: True & False
(i) Very small numbers can be expressed in standard form using negative exponents.
(ii) ap × bq = (ab)pq
(iii) .00567 = 5.67×10−3
(iv) 1/(8)−3 = 29
(v) 40 = 4
(vi) (−1)3 = 1
(vii) The multiplicative inverse of (–2)–2 is (2)2.
Ans:
(i) True
(ii) False
(iii) True
(iv) True
(v) False
(vi) False
(vii) True as (–2)–2 = 1/4
Q7: Match the column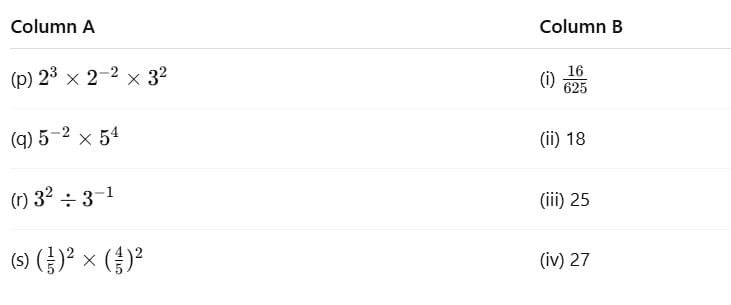
Ans: (p) 23×2−2×32
= 23−2 × 32 = 21 × 9 = 18(q) 5−2 × 54
= 5−2+4 =52 =25(r) 32÷3−1
= 32−(−1) =33 = 27(s)
Therefore correct match is :
(p) → (ii)
(q) → (iii)
(r) → (iv)
(s) → (i)
Q8: The multiplicative inverse of (–7)–2 ÷ (90)–1 is
(a) −(7)2 × (90)–1
(b) −(7)−2 × (90)–1
(c) −(7)2 ÷ (90)–1
(d) −(7)2 × (90)1
Ans: (a)
Sol: (–7)–2 ÷ (90)–1= −(1/7)2 × 901.
So Multiplication inverse is −(7)2 × (90)–1.
Hence correct Option is (a)
Q9: If a be any non-zero integer, then a–1 is equal to
(a) a
(b) -a
(c) 1/a
(d) -1/a
Ans: (c)
Q10: If 53x–1 ÷ 25 = 125, Then the value x is
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol:
Express 25 and 125 as powers of 5
So the equation becomes:
Apply the laws of exponents
Now, equating powers (since bases are same):3x − 3 = 3
⇒ 3x = 6
⇒x=2Hence x = 2
Option(b) is correct.
Q11: Simplify and express the result in power notation with positive exponent.
(i) (-2)5 ÷ (-2)4
(ii) (1/2)2 × (2/5)2
(iii) (-5)2 × (3/5)
Sol:
(i) (-2)5 ÷ (-2)4
= (-2)5 / (-2)4
= (-2)5-4
=(-2)(ii) (1/2)2 × (2/5)2
= (1/4) X (4/25)
= 1/25(iii) (-5)2 × (3/5)
= 25 × (3/5)
= 15
Q12: Find the value of x here
Sol:
Q13: Express the following numbers in standard form.
(i) 0.0000000015
(ii) 0.00000001425
(iii) 102000000000000000
Sol:
(i) 0.0000000015 = 1.5 ×10-9
(ii) 0.00000001425 = 1.425×10-8
(iii) 102000000000000000 = 1.02×1017
Q14: Solve for the variables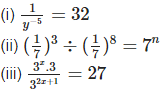
Sol:
Q15: Simplify the following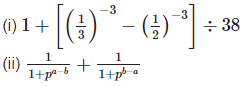
Sol:
|
81 videos|423 docs|31 tests
|
FAQs on Important Questions for Class 8 Maths - Exponents and Powers
| 1. What are exponents and how are they used in mathematical expressions? |  |
| 2. How do you multiply numbers with exponents? |  |
| 3. What is the rule for dividing numbers with exponents? |  |
| 4. How do you evaluate a power of zero, such as \(a^0\)? |  |
| 5. What are some real-life applications of exponents and powers? |  |