Important Questions: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Q1: What is the maximum exterior angle possible for a regular polygon?
Sol: To find:- The maximum exterior angle possible for a regular polygon.
A polygon with minimum sides is an equilateral triangle.
So, the number of sides = 3
The sum of all exterior angles of a polygon is 360°
Exterior angle = 360°/Number of sides
Therefore, the maximum exterior angle possible will be
= 360°/3
= 120°
Q2: Find the measure of angles P and S if SP and RQ are parallel.
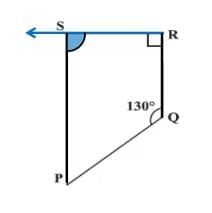
Sol:
∠P + ∠Q = 180° (angles on the same side of transversal)
∠P + 130° = 180°
∠P = 180° – 130° = 50°
also, ∠R + ∠S = 180° (angles on the same side of transversal)
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Thus, ∠P = 50° and ∠S = 90°
Yes, there is more than one method to find m∠P.
PQRS is a quadrilateral. The sum of measures of all angles is 360°.
Since we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310°
= 50°
Q3: Triangle ABC is a right-angled triangle, and O is the midpoint of the side opposite to the right angle. State why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).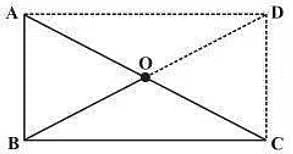
Sol: AD and DC are drawn in such a way that AD is parallel to BC and AB is parallel to DC
AD = BC and AB = DC
ABCD is a rectangle since the opposite sides are equal and parallel to each other, and the measure of all the interior angles is altogether 90°.
In a rectangle, all the diagonals bisect each other and are of equal length.
Therefore, AO = OC = BO = OD
Hence, O is equidistant from A, B and C.
Q4: State whether true or false.
(a) All the rectangles are squares.
(b) All the rhombuses are parallelograms.
(c) All the squares are rhombuses and also rectangles.
(d) All the squares are not parallelograms.
(e) All the kites are rhombuses.
(f) All the rhombuses are kites.
(g) All the parallelograms are trapeziums.
(h) All the squares are trapeziums.
Sol:
(a) This statement is false.
A rectangle has opposite sides equal and all angles equal to 90 degrees, but for it to be a square, all four sides must be equal. Therefore, not all rectangles are squares.
(b) This statement is true.
A rhombus is a type of parallelogram where all four sides are of equal length. Since it has both pairs of opposite sides parallel, it is always a parallelogram.
(c) This statement is true.
A square has all properties of a rhombus (all sides equal) and a rectangle (all angles 90 degrees). Therefore, all squares are both rhombuses and rectangles.
(d) This statement is false.
A square is a specific type of parallelogram where all sides are equal and all angles are right angles. Therefore, all squares are parallelograms.
(e) This statement is false.
A kite has two pairs of adjacent sides equal, but not all four sides need to be equal. For it to be a rhombus, all four sides must be equal. Therefore, not all kites are rhombuses.
(f) This statement is true.
A rhombus has all four sides equal, which satisfies the condition of a kite having two pairs of adjacent sides equal. Therefore, all rhombuses are kites.
(g) This statement is false.
A parallelogram has both pairs of opposite sides parallel, and a trapezium is a quadrilateral with exactly one pair of parallel sides. Since parallelograms have two pairs of parallel sides, they do not meet this criterion and are not considered trapeziums.
(h) This statement is true.
A square has both pairs of opposite sides parallel, which means it satisfies the condition of a trapezium having at least one pair of parallel sides. Therefore, all squares are trapeziums.
Q5: The two adjacent angles of a parallelogram are the same. Find the measure of each and every angle of the parallelogram.
Sol: A parallelogram with two equal adjacent angles.
To find:- the measure of each of the angles of the parallelogram.
The sum of all the adjacent angles of a parallelogram is supplementary.
∠A + ∠B = 180°
2∠A = 180°
∠A = 90°
∠B = ∠A = 90°
In a parallelogram, the opposite sides are the same.
Therefore,
∠C = ∠A = 90°
∠D = ∠B = 90°
Hence, each angle of the parallelogram measures 90°.
Q6: ABCD is a parallelogram in which ∠A = 110°. Find the measure of the angles B, C and D, respectively.
Sol: The measure of angle A = 110°
the sum of all adjacent angles of a parallelogram is 180°
∠A + ∠B = 180
110°+ ∠B = 180°
∠B = 180°- 110°
= 70°.
Also ∠B + ∠C = 180° [Since ∠B and ∠C are adjacent angles]
70° + ∠C = 180°
∠C = 180°- 70°
= 110°.
Now ∠C + ∠D = 180° [Since ∠C and ∠D are adjacent angles]
110° + ∠D = 180°
∠D = 180°- 110°
= 70°
Q7: The measure of the two adjacent angles of the given parallelogram is the ratio of 3:2. Then, find the measure of each angle of the parallelogram.
Sol: A parallelogram with adjacent angles in the ratio of 3:2
To find:- The measure of each of the angles of the parallelogram.
Let the measure of angle A be 3x
Let the measure of angle B be 2x
Since the sum of the measures of adjacent angles is 180° for a parallelogram,
∠A+∠B=180°
3x+2x=180°
5x=180°
x=36°
∠A=∠C =3x=108°
∠B=∠D =2x=72° (Opposite angles of a parallelogram are equal).
Hence, the angles of a parallelogram are 108°, 72°,108°and 72°
Q8: Adjacent sides of a rectangle are in the ratio 5: 12; if the perimeter of the given rectangle is 34 cm, find the length of the diagonal.
Sol: The ratio of the adjacent sides of the rectangle is 5: 12
Let 5x and 12x be adjacent sides.
The perimeter is the sum of all the given sides of a rectangle.
5x + 12x + 5x + 12x = 34 cm ……(since the opposite sides of the rectangle are the same)
34x = 34
x = 34/34
x = 1 cm
Therefore, the adjacent sides of the rectangle are 5 cm and 12 cm, respectively.
That is,
Length =12 cm
Breadth = 5 cm
Length of the diagonal = √( l2 + b2)
= √( 122 + 52)
= √(144 + 25)
= √169
= 13 cm
Hence, the length of the diagonal of a rectangle is 13 cm.
Q9: Find the measure of all the exterior angles of a regular polygon with
(i) 9 sides and
(ii) 15 sides.
Sol: (i) Total measure of all exterior angles = 360°
Each exterior angle =sum of exterior angle = 360° = 40°
number of sides 9
Each exterior angle = 40°
(ii) Total measure of all exterior angles = 360°
Each exterior angle = sum of exterior angle =360° = 24°
number of sides 15
Each exterior angle = 24°
Q10: A quadrilateral has three acute angles, each measuring 80°. What is the measure of the fourth angle of the quadrilateral?
Sol:– Let x be the measure of the fourth angle of a quadrilateral.
The sum of all the angles of a quadrilateral + 360°
80° + 80° + 80° + x = 360° …………(since the measure of all the three acute angles = 80°)
240° + x = 360°
x = 360° – 240°
x = 120°
Hence, the fourth angle made by the quadrilateral is 120°.
Q11: How many sides do regular polygons consist of if each interior angle is 165°?
Sol: A regular polygon with an interior angle of 165°
We need to find the sides of the given regular polygon:-
The sum of all exterior angles of any given polygon is 360°.
Formula Used: Number of sides = 360∘ /Exterior angle
Exterior angle = 180∘−Interior angle
Thus,
Each interior angle = 165°
Hence, the measure of every exterior angle will be
= 180° − 165°
= 15°
Therefore, the number of sides of the given polygon will be
= 360°/15°
= 24 sides
Q12: ABCD is a parallelogram with ∠A = 80°. The internal bisectors of ∠B and ∠C meet each other at O. Find the measure of the three angles of ΔBCO.
Sol: The measure of angle A = 80°.
In a parallelogram, the opposite angles are the same.
Hence,
∠A = ∠C = 80°
And
∠OCB = (1/2) × ∠C
= (1/2) × 80°
= 40°
∠B = 180° – ∠A (the sum of interior angles situated on the same side of the transversal is supplementary)
= 180° – 80°
= 100°
Also,
∠CBO = (1/2) × ∠B
∠CBO= (1/2) × 100°
∠CBO= 50°.
By the property of the sum of the angle BCO, we get,
∠BOC + ∠OBC + ∠CBO = 180°
∠BOC = 180° – (∠OBC + CBO)
= 180° – (40° + 50°)
= 180° – 90°
= 90°
Hence, the measure of all the angles of triangle BCO is 40°, 50° and 90°.
Q13: Is it ever possible to have a regular polygon, each of whose interior angles is 100?
Sol: The sum of all the exterior angles of a regular polygon is 360°
As we also know, the sum of interior and exterior angles are 180°
Exterior angle + interior angle = 180 - 100 = 80°
When we divide the exterior angle, we will get the number of exterior angles since it is a regular polygon means the number of exterior angles equals the number of sides.
Therefore n = 360/ 80 = 4.5
And we know that 4.5 is not an integer, so having a regular polygon is impossible.
Whose exterior angle is 100°
Q14: A diagonal and a side of a rhombus are of equal length. Find the measure of the angles of the rhombus.
Sol: One of the diagonals of a rhombus is equal to one of its sides.
We know that a rhombus has four equal sides. If one side has the same length as a diagonal, the diagonal is part of two equilateral triangles.Since a rhombus has four sides we can say
Rhombus = ABCD where AB = diagonal of AC
Since the triangle ABC is equilateral and so angle ABC = 60. To solve the problem we can make an equation.
60 + x = 180
180 - 60 = x
x = 120
so, angles of rhombus are:
60,120,60,120
Q15: The measures of the two adjacent angles of a parallelogram are in the given ratio 3: 2. Find the measure of every angle of the parallelogram.
Sol: Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x, respectively, in parallelogram ABCD.
∠A + ∠B = 180°
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
The opposite sides of a parallelogram are the same.
∠A = ∠C = 3x = 3 × 36° = 108°
∠B = ∠D = 2x = 2 × 36° = 72°
|
22 videos|133 docs|11 tests
|
FAQs on Important Questions: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the key concepts covered in "A Story of Numbers"? |  |
| 2. How do prime numbers differ from composite numbers? |  |
| 3. Why are numbers important in various fields such as science and technology? |  |
| 4. How can understanding number properties help in solving mathematical problems? |  |
| 5. What role do numbers play in everyday life? |  |
















