Important Questions: Relations & Functions | Mathematics (Maths) Class 11 - Commerce PDF Download
Q1: The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.
Ans: We know that,
If n(A) = p and n(B) = q, then n(A × B) = pq
From the given,
n(A × A) = 9
n(A) × n(A) = 9,
n(A) = 3 ……(i)
The ordered pairs (-1, 0) and (0, 1) are two of the nine elements of A × A.
Therefore, A × A = {(a, a) : a ∈ A}
Hence, -1, 0, 1 are the elemets of A. …..(ii)
From (i) and (ii),
A = {-1, 0, 1}
The remaining elements of set A × A are (-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0) and (1, 1).
Q2: Assume that A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, such that x, y ∈ A}. Determine and write down its range, domain, and codomain.
Ans: It is given that the relation R from A to A is given by R = {(x, y): 3x – y = 0, where x, y ∈ A}.
It means that R = {(x, y) : 3x = y, where x, y ∈ A}
Hence, R = {(1, 3), (2, 6), (3, 9), (4, 12)}
We know that the domain of R is defined as the set of all first elements of the ordered pairs in the given relation.
Hence, the domain of R = {1, 2, 3, 4}
To determine the codomain, we know that the entire set A is the codomain of the relation R.
Therefore, the codomain of R = A = {1, 2, 3,…,14}
As it is known that, the range of R is defined as the set of all second elements in the relation ordered pair.
Hence, the Range of R is given by = {3, 6, 9, 12}
Q3: Redefine the function: f(x) = |x – 1| – |x + 6|. Write its domain also.
Ans: Given function is f(x) = |x – 1| – |x + 6|
Redefine of the function is: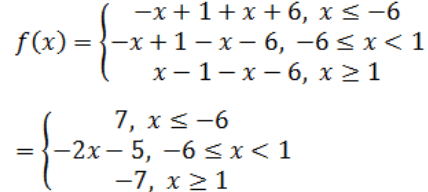
The domain of this function is R.
Q4: Find the domain and range of the real function f(x) = x/1+x2.
Ans: Given real function is f(x) = x/1+x2.
1 + x2 ≠ 0
x2 ≠ -1
Domain : x ∈ R
Let f(x) = y
y = x/1+x2
⇒ x = y(1 + x2)
⇒ yx2 – x + y = 0
This is a quadratic equation with real roots.
(-1)2 – 4(y)(y) ≥ 0
1 – 4y2 ≥ 0
⇒ 4y2 ≤ 1
⇒ y2 ≤1/4
⇒ -½ ≤ y ≤ ½
⇒ -1/2 ≤ f(x) ≤ ½
Range = [-½, ½]
Q5: Write the range of a Signum function.
Ans: The real function f: R → R defined by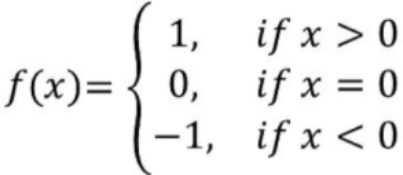
is called the signum function. Domain of f = R, Range of f = {1, 0, – 1}
Q6: Express the function f: A—R. f(x) = x2 – 1. where A = { -4, 0, 1, 4) as a set of ordered pairs.
Ans: Given,
A = {-4, 0, 1, 4}
f(x) = x2 – 1
f(-4) = (-4)2 – 1 = 16 – 1=15
f(0) = (0)2 – 1 = -1
f(1) = (1)2 – 1 = 0
f(4) = (4)2 – 1 = 16 – 1 =15
Therefore, the set of ordered pairs = {(-4, 15), (0, -1), (1, 0), (4, 15)}
Q7: Let f(x) = x2 and g(x) = 2x + 1 be two real functions. Find
(f + g) (x), (f –g) (x), (fg) (x), (f/g ) (x)
Ans: Given,
f(x) = x2 and g(x) = 2x + 1
(f + g) (x) = x2 + 2x + 1
(f – g) (x) = x2 -(2x + 1) = x2 – 2x – 1
(fg) (x) = x2(2x + 1) = 2x3 + x2
(f/g) (x) = x2/(2x + 1), x ≠ -1/2
Q8: The function f is defined by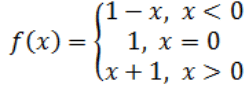
Draw the graph of f(x).
Ans: f(x) = 1 – x, x < 0, this gives
f(– 4) = 1 – (– 4)= 5;
f(– 3) =1 – (– 3) = 4,
f(– 2) = 1 – (– 2)= 3
f(–1) = 1 – (–1) = 2; etc,
Also, f(1) = 2, f (2) = 3, f (3) = 4, f(4) = 5 and so on for f(x) = x + 1, x > 0.
Thus, the graph of f is as shown in the below figure.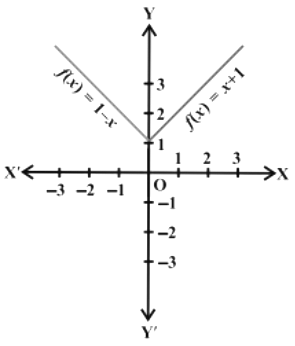
|
80 videos|315 docs|99 tests
|
















