Important Questions: Three Dimensional Geometry | Mathematics (Maths) Class 12 - JEE PDF Download
Q1: Show that the points A (2, 3, – 4), B (1, – 2, 3) and C (3, 8, – 11) are collinear.
Ans: We know that the direction ratios of the line passing through two points P(x1, y1, z1) and Q(x2, y2, z2) are given by:
x2 – x1, y2 – y1, z2 – z1 or x1 – x2, y1 – y2, z1 – z2
Given points are A (2, 3, – 4), B (1, – 2, 3) and C (3, 8, – 11).
Direction ratios of the line joining A and B are:
1 – 2, – 2 – 3, 3 + 4
i.e. – 1, – 5, 7.
The direction ratios of the line joining B and C are:
3 –1, 8 + 2, – 11 – 3
i.e., 2, 10, – 14.
From the above, it is clear that direction ratios of AB and BC are proportional.
That means AB is parallel to BC. But point B is common to both AB and BC.
Hence, A, B, C are collinear points.
Q2: Find the angle between the pair of lines given by
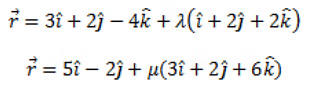
Ans:
From the given,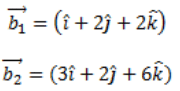
Let θ be the angle between the given pair of lines.
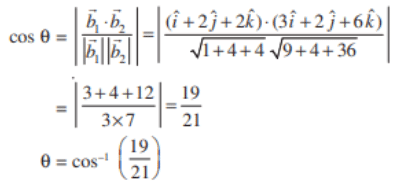
Q3: Find the distance between the lines l1 and l2 given by:
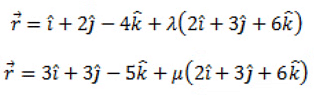
Ans: Given two lines are parallel.
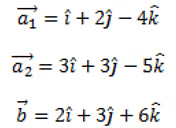
The distance between the two given lines is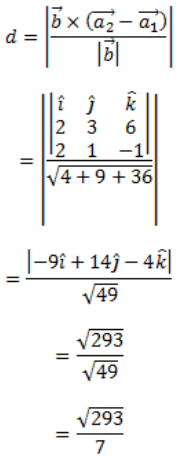
Q4: Find the intercepts cut off by the plane 2x + y – z = 5.
Ans: Given plane is 2x + y – z = 5 ……(i)
Dividing both sides of the equation (i) by 5,
(⅖)x + (y/5) – (z/5) = 1
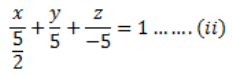
We know that,
The equation of a plane in intercept form is (x/a) + (y/b) + (z/c) = 1, where a, b, c are intercepts cut off by the plane at x, y, z-axes respectively.
For the given equation,
a = 5/2, b = 5, c = -5
Hence, the intercepts cut off by the plane are 5/2, 5 and -5.
Q5: Find the direction cosines of the line passing through the two points (– 2, 4, – 5) and (1, 2, 3).
Ans: We know that the direction cosines of the line passing through two points P(x1, y1, z1) and Q(x2, y2, z2) are given by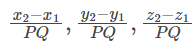
Using the distance formula,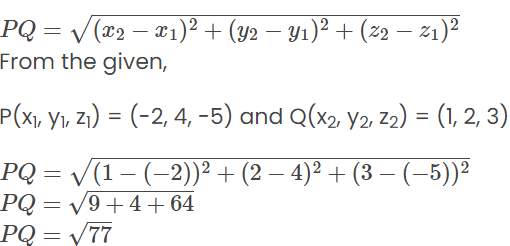
Hence, the direction cosines of the line joining the given two points are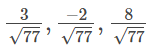
Q6: If a line makes angles 90°, 135°, 45° with the x, y and z-axes respectively, find its direction cosines.
Ans: Let the direction cosines of the line be l, m, and n.
l = cos 90° = 0
m = cos 135° = -1/√2
n = cos 45° = 1/√2
Hence, the direction cosines of the line are 0, -1/√2, and 1/√2.
Q7: Find the angle between the pair of lines given below.
(x + 3)/3 = (y -1)/5 = (z + 3)/4
(x + 1)/1 = (y – 4)/1 = (z – 5)/2
Ans: Given,
(x + 3)/3 = (y -1)/5 = (z + 3)/4
(x + 1)/1 = (y – 4)/1 = (z – 5)/2
The direction ratios of the first line are:
a1 = 3, b1 = 5, c1 = 4
The direction ratios of the second line are:
a2 = 1, b2 = 1, c2 = 2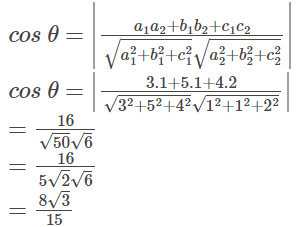
Hence, the required angle is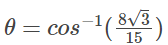
Q8: Show that the lines (x – 5)/7 = (y + 2)/-5 = z/1 and x/1 = y/2 = z/3 are perpendicular to each other.
Ans: Given lines are:
(x – 5)/7 = (y + 2)/-5 = z/1 and x/1 = y/2 = z/3
The direction ratios of the given lines are 7, -5, 1 and 1, 2, 3, respectively.
We know that,
Two lines with direction ratios a1, b1, c1 and a2, b2, c2 are perpendicular to each other if a1a2 + b1b2 + c1c2 = 0
Therefore, 7(1) + (-5) (2) + 1 (3)
= 7 – 10 + 3
=0
Hence, the given lines are perpendicular to each other.
Q9: Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), and (– 2, 2, – 1).
Ans: Given points are (1, 1, 0), (1, 2, 1), and (– 2, 2, – 1).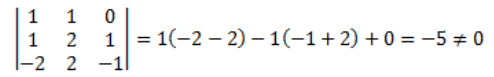
Therefore, the plane will pass through the given three points.
We know that,
The equation of the plane through the points (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is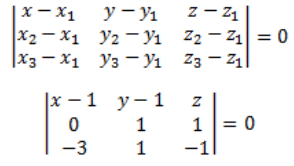
(x – 1)(-2) -(y – 1) (3) + z (3) = 0
-2x + 2 – 3y + 3 + 3z = 0
-2x – 3y + 3z + 5 = 0
-2x – 3y + 3z = -5
Therefore, 2x + 3y – 3z = 5 is the required Cartesian equation of the plane.
|
203 videos|307 docs|139 tests
|
FAQs on Important Questions: Three Dimensional Geometry - Mathematics (Maths) Class 12 - JEE
| 1. What is three-dimensional geometry? |  |
| 2. What are the coordinates of a point in three-dimensional space? |  |
| 3. How do you calculate the distance between two points in three-dimensional space? |  |
| 4. What are the different types of lines in three-dimensional space? |  |
| 5. How do you find the equation of a plane in three-dimensional space? |  |





















