Important Questions: Vectors | Mathematics (Maths) Class 12 - JEE PDF Download
Q1: Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
Ans: Vertices of a triangle ABC are A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
Let AB and BC be the adjacent sides of triangle ABC.
Hence, the area of triangle ABC is √61/2 sq.units.
Q2: Evaluate the product.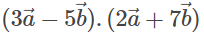
Ans: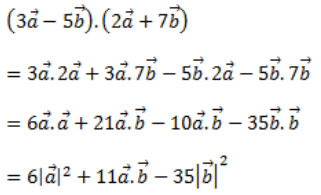
Q3: Show that the points A, B and C with position vectors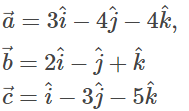
form the vertices of a right-angled triangle.
Ans: Position vectors of points A, B and C are respectively given as below.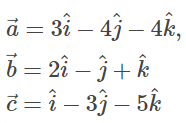
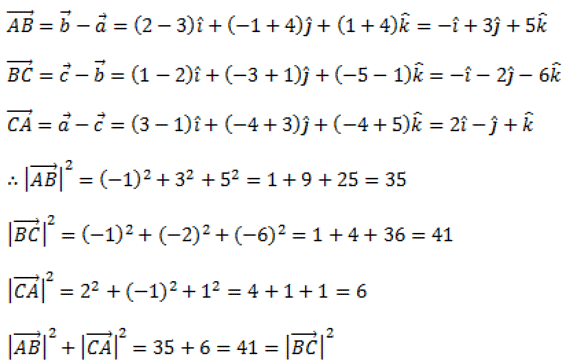
Therefore, ABC is a right-angled triangle.
Q4: Find a vector in the direction of a vector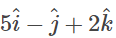 which has a magnitude of 8 units.
which has a magnitude of 8 units.
Ans: Let 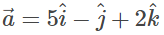
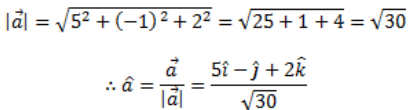
Q5: Find the unit vector in the direction of the sum of the vectors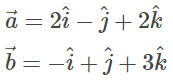
Ans: Let  be the sum of
be the sum of
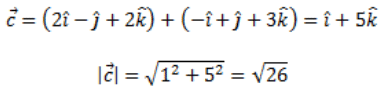
The unit vector is: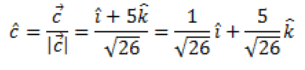
Q6: Find all vectors of magnitude 10√3 that are perpendicular to the plane of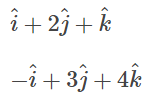
Ans:
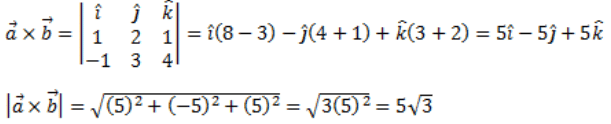
Hence, the unit vector perpendicular to the plane of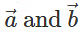 is:
is: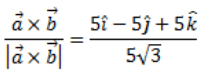
Therefore, the vectors of magnitude 10√3 that are perpendicular to the plane of 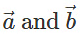 are:
are:
Q7: Find a vector 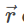 of magnitude 3√2 units which makes an angle of π/4, π/2 with y and z-axes, respectively.
of magnitude 3√2 units which makes an angle of π/4, π/2 with y and z-axes, respectively.
Ans: From the given,
m = cos π/4 = 1/√2
n = cos π/2 = 0
Therefore, l2 + m2 + n2 = 1
l2 + (½) + 0 = 1
l2 = 1 – ½
l = ±1/√2
Hence, the required vector is: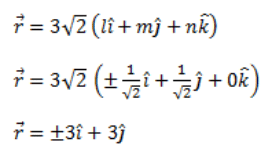
Q8: Show that the vector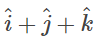 is equally inclined to the axes OX, OY and OZ.
is equally inclined to the axes OX, OY and OZ.
Ans: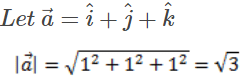
Therefore, the direction cosines of 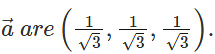
Let α, β,γ be the angles formed by  the positive directions of x, y, and z-axes.
the positive directions of x, y, and z-axes.
cos α = 1/√3, cos β = 1/√3 cos γ = 1/√3
Hence, the given vector is equally inclined to axes OX, OY and OZ.
Q9: Find the vector joining the points P(2, 3, 0) and Q(– 1, – 2, – 4) directed from P to Q.
Ans: Since the vector is to be directed from P to Q, clearly P is the initial point and Q is the terminal point.
P(2, 3, 0) = (x1, y1, z1)
Q(-1, -2, -4) = (x2, y2, z2)
Vector joining the points P and Q is: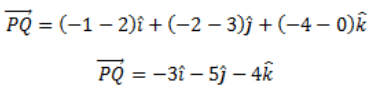
Q10: Represent graphically a displacement of 40 km, 30° east of north.
Ans: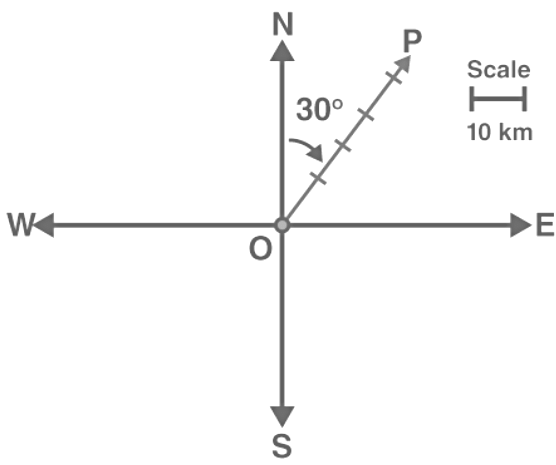
Hence, the vector OP represents the displacements of 40 km, 30° east of north.
|
203 videos|307 docs|139 tests
|
















