Important Definitions & Formulas: Quadratic Equations | Mathematics (Maths) Class 10 PDF Download
The chapter on quadratic equations is essential because it equips us with a versatile problem-solving tool that finds applications in countless real-life situations.
This document provides Class 10 Maths Formulas for Pair of Quadratic Equations that can greatly assist you in excelling in your board exams and future competitive examinations.
Important Definitions
1. Standard Form of a Quadratic Equation
The standard/general form of a quadratic equation is ax2 + bx + c = 0 where,
a ≠ 0 and a, b, c are real numbers.
In this equation, the variable is ‘x’ and the degree of the equation is ‘2.’
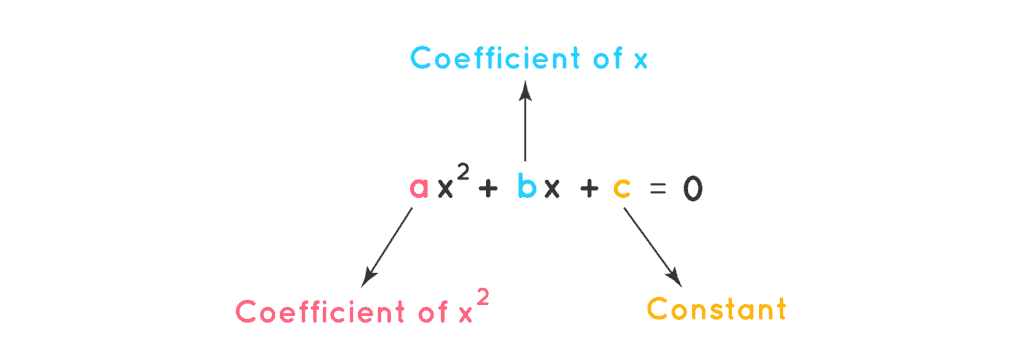 Standard Form of Quadratic Equation
Standard Form of Quadratic Equation
2. Zeroes & Roots of the Quadratic Equation
The values of x for which a quadratic equation is satisfied are called the roots/zeroes of the quadratic equation.
If α is a root of the quadratic equation ax2+bx+c=0, then aα2+bα+c=0.
A quadratic equation can have two distinct real roots, two equal roots or real roots may not exist.
Graphically, the roots of a quadratic equation are the points where the graph of the quadratic polynomial cuts the x-axis.
Example: Consider y = x2 - 8x +12
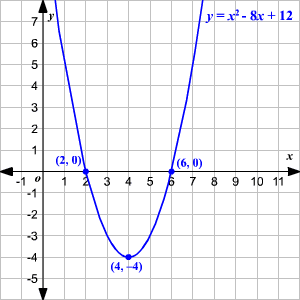
The graph of the above quadratic equation is intersecting the x-axis at two points. So, the given quadratic equation has two distinct real roots.
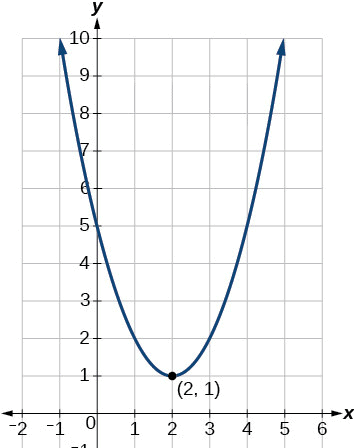 The above quadratic equation is not intersecting the x-axis at any point. So the roots of the given quadratic equation are not real.
The above quadratic equation is not intersecting the x-axis at any point. So the roots of the given quadratic equation are not real.
Also, consider y = x2
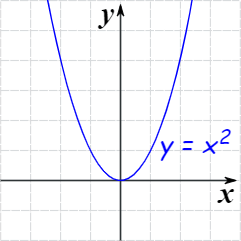
The curve of y = x2 is intersecting the x-axis at only one point. So, the above equation has real but repeated roots.
Important Methods and Formulas
1. Solving Quadratic Equations with Factorisation Method
This method is also known as splitting the middle-term method.
Let's see with an appropriate example.
 Solving Quadratic Equations By Factorising
Solving Quadratic Equations By Factorising
Example: Solve x2 + 3x - 4 = 0
Step 1: Compare it with the standard form of the quadratic equation ax2 + bx + c = 0
Here, a = 1, b = 3, c = -4. Let us multiply a and c = 1 x (-4) = -4.
Step 2: Next, the middle term is split into two terms. We do it such that the product of the new coefficients equals the product of a and c.
We have to get 3 here. Consider (+4) and (-1) as the factors, whose multiplication is -4 and sum is 3. Hence, we write x2 + 3x – 4 = 0 as x2 + 4x – x – 4 = 0.
Thus, we can factorise the terms as: (x + 4)(x - 1) = 0.
For any two quantities a and b, if a×b = 0, we must have either a = 0, b = 0 or a = b = 0.
Thus we have either (x + 4) = 0 or (x - 1) = 0 or both are = 0. This gives x + 4 = 0 or x - 1 = 0. Solving these equations for x gives x=-4 or x=1.
2. Quadratic Formula
This is the most powerful method for solving quadratic equations. This method will work for every quadratic equation. This is the general quadratic equation formula. We define it as follows: If ax2 + bx + c = 0 is a quadratic equation, then the value of x is given by the following formula:
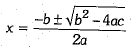
Just plug in the values of a, b and c, and do the calculations. The quantity in the square root is called the discriminant or D.
The roots of the quadratic equation ax2 + bx + c = 0, a ≠ 0 can be found by using the following formula if its discriminant (D = b2 - 4ac) is greater than or equal to zero.
3. Nature of Roots
Based on the value of the discriminant, D=(b2 − 4ac), the roots of a quadratic equation can be of three types. Case 1: If D>0, the equation has two distinct real roots.
Case 1: If D>0, the equation has two distinct real roots.
Case 2: If D=0, the equation has two equal real roots.
Case 3: If D<0, the equation has no real roots.
Word Problem Solved Examples
Example 1: A shopkeeper buys some books for 80. If he had bought 4 more books for the same amount, each book would have cost ₹1 less. Find the number of books he bought.
Solution: Let the number of books he bought = x
Increased number of books he had bought = x + 4
Total amount = ₹80
According to the problem,
⇒ x(x + 4) = 320
⇒ x2 + 4x – 320 = 0
⇒ x2 + 20x – 16x – 320 = 0
⇒ x(x + 20) – 16(x + 20) = 0
⇒ (x + 20) (x – 16) = 0
⇒ x + 20 = 0 or x – 16 = 0
⇒ x = -20 … (neglected) or x = 16∴ Number of books he bought = 16
Example 2: The sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Solution: Let the side of Large square = x cm
Let the side of small square = y cm
According to the Question,
x2 + y2 = 400… (i) …[∵ area of square = (side)2
4x – 4y = 16 …[∵ Perimeter of square = 4 sides
⇒ x – y = 4 … [Dividing both sides by 4
⇒ x = 4 + y …(ii)
Putting the value of x in equation (i),
(4 + y)2 + y2 = 400
⇒ y2 + 8y + 16 + y2 – 400 = 0
⇒ 2y2 + 8y – 384 = 0
⇒ y2 + 4y – 192 = 0 … [Dividing both sides by 2
⇒ y2 + 16y – 12y – 192 = 0
⇒ y(y + 16) – 12(y + 16) = 0
⇒ (y – 12)(y + 16) = 0
⇒ y – 12 = 0 or y + 16 = 0
⇒ y = 12 or y = -16 … [Neglecting negative value|
∴ Side of small square = y = 12 cm
and Side of large square = x = 4 + 12 = 16 cm
Example 3: The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
Solution: Let the length of the shorter side be x m.
∴ length of diagonal = (x + 16) m
and length of longer side = (x + 14) m
Using Pythagoras theorem,
(l)2 + (b)2 = (h)2
∴ x2 + (x + 14)2 = (x + 16)2
⇒ x2 + x2 + 196 + 28x = x2 + 256 + 32x
⇒ x2 – 4x – 60 = 0
⇒ x2 – 10x + 6x – 60 = 0
⇒ x(x – 10) + 6(x – 10) = 0
⇒ (x – 10) (x + 6) = 0
⇒ x – 10 = 0 or x + 6 = 0
⇒ x = 10 or x = -6 (Reject)
⇒ x = 10 m …[As length cannot be negative
Length of shorter side = x = 10 m
Length of diagonal = (x + 16) m = 26 m
Length of longer side = (x + 14)m = 24m
∴ Lengths of the sides are 10 m and 24 m.
Example 4: The sum of three numbers in A.P. is 12 and sum of their cubes is 288. Find the numbers.
Solution: Let three numbers in A.P. be a – d, a, a + d.
a – d + a + a + d = 12
⇒ 3a = 12 ⇒a = 4
(a – d)3 + (a)3 + (a + d)3 = 288
⇒ a3 – 3a2d + 3ad2 – d3 + a3 + a3 + 3a2d + 3ad2 + d3 = 288
⇒ 3a3 + 6ad2 = 288
⇒ 3a(a2 + 2d2) = 288
⇒ 3 × 4(42 + 2d2) = 288
⇒ (16 + 2d2) = 28812
⇒ 2d2 = 24 – 16 = 8
⇒ d2 = 4 ⇒ d = ± 2
When, a = 4, d = 2, numbers are –
a – d, a, a + d, i.e., 2, 4, 6
When, a = 4, d = -2, numbers are –
a – d, a, a + d, i.e., 6, 4, 2
Example 5: The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
Solution: Perimeter of right ∆ = 60 cm …[Given
a + b + c = 60
a + b + 25 = 60
a + b = 60 – 25 = 35 …(I)
In rt. ∆ACB, AC2 + BC2 = AB2
b2 + a2 = (25)2 …[Pythagoras’ theorem|
a2 + b2 = 625 ….(ii)
From (i), a + b = 35
(a + b)2 = (35) … [Squaring both sides
a2 + b2 + 2ab = 1225
625 + 2ab = 1225 … [From (ii)
2ab = 1225 – 625 = 600 ⇒ ab = 300 … (iii)
Area of ∆ = 12 × base × corresponding altitude
= 12 × b × a = 12 (300) ..[From (iii)
= 150 cm2
|
127 videos|584 docs|79 tests
|
FAQs on Important Definitions & Formulas: Quadratic Equations - Mathematics (Maths) Class 10
| 1. What is the standard form of a quadratic equation? |  |
| 2. How are the zeroes or roots of a quadratic equation determined? |  |
| 3. How can quadratic equations be solved using the factorisation method? |  |
| 4. What is the quadratic formula and how is it used to solve quadratic equations? |  |
| 5. What is the nature of roots of a quadratic equation and how can it be determined? |  |

















