Initial and boundary value problems | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download

Definition of an Initial-Value Problem

where $(a,\; b)$ is the point the solution y(x) must go through. 

First Order Differential Equation Initial Value Problem

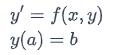
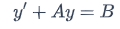
where A and B are real numbers with A ≠ 0. Remember that the general solution to this linear differential equation is 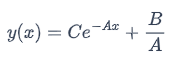where C  is a constant.

If you add the initial value 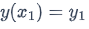 where x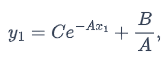$\mathrm{<sub\; style="word-break:\; break-word;\; line-height:\; 1.8;\; color:\; black;\; letter-spacing:\; inherit\; !important;">1</sub>}$ and y$\mathrm{<sub\; style="word-break:\; break-word;\; line-height:\; 1.8;\; color:\; black;\; letter-spacing:\; inherit\; !important;">1</sub>}$ are real numbers, then you can plug those into the general solution to get So,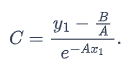That means the solution to the IVP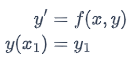

is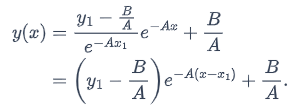

Initial value Problems and Separable Differential Equations

where N(y) and M(x) are functions. For more information and examples of this kind of equation see Separable Equations. 
To make this into an IVP, all you need to do is pick an initial value. So for real numbers a and b, the IVP is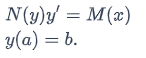 

With separable equations, you often need to be careful with the interval of existence for solutions. In cases like that, the initial value tells you which of the intervals to choose as the interval of existence. 

Let's take a look at an example.
Example: If possible, solve the IVP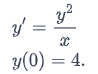

Solution: First, you can rewrite the differential equation as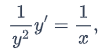so it is a separable differential equation. Separating variables and integrating gives you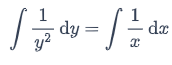

soNow let's try and use the initial conditions. If you do, you will be using x = 0, and you can't take the natural log of zero. So in fact this IVP has no solution.

One more example, to see the kinds of things that can happen.
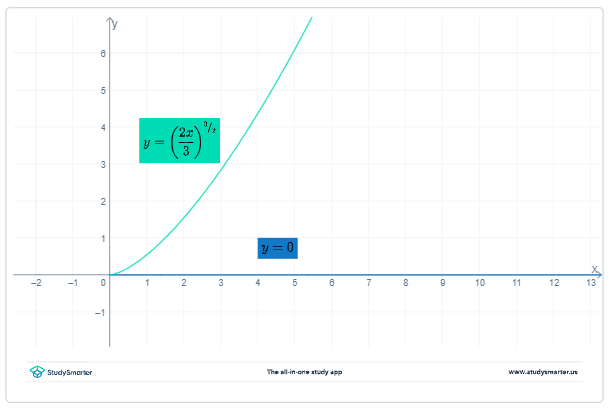
Example: Consider the IVP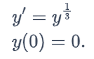First show that the constant solution y(x) = 0 satisfies this IVP. Then see if there are any other solutions.

Solution: Certainly if you take the derivative of a constant function you get zero, and $0\frac{1}{3}=0$, so the constant function $𝑦\left(𝑥\right)=0$ satisfies the differential equation. It also satisfies the initial condition, so it does satisfy the IVP.
What about other solutions? This is a separable equation, so separating and integrating gives you

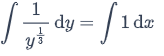
so

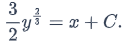
Using the initial value y$\left(0\right)=0$ to find C, you get

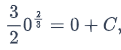
so C$=0$. That means there is a second solution to this IVP, namely the implicit solution

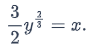
You can get the explicit solution by solving for y. If you do, you get

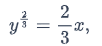
so

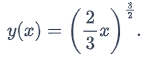
Notice that the maximal interval of existence is $[0,\infty )$ since you can't take the square root of a negative number. If you graph the two functions, you can see that both the constant function and the function y(x) that you solved for both satisfy the equation and the initial value.

More Solved Examples

Q1. Consider the problem y' = (1 - y²)¹⁰ cos y, y(0) = 0. Let J be the maximal interval of existence and K be the range of the solution of the above problem. Then which of the following statements are true?
Solution:  
Concept -
(1) If f is bounded and continuously differentiable on R then maximum interval of existence is R.
We have y' = (1 - y2)10 cos y, y(0) = 0.
Now f(x,y) = (1 - y2)10  cos y
Clearly f is continuous and differentiable function.
Now |f| ≤ (1 - y2)10 ≤ M  ∀ y ∈ R
Hence f is bounded as well
Therefore maximum interval of existence is R.
Now the function f = (1 - y2)10  cos y is even function as (1 - y2)10 is even and  cos y is also even function.
⇒ y' = even
⇒ y = odd 
Let assume y = x is odd function.
Now 1 = (1 - x2)10  cos x
Now according to the options, we take x = 1
then equation is not satisfied 1 ≠ 0
Hence the range of the solution (-1,1)

Q2. Consider the following initial value problem 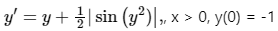. Which of the following statements are true?
Solution: 
We have 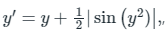$𝑦\prime =𝑦+\frac{1}{2}|\sin (𝑦2\left)\right|,$, x > 0, y(0) = -1
If a solution exist for the differential equation then Lipchitz condition is satisfied.
Now $𝑦\prime -𝑦=\frac{1}{2}|\sin (𝑦2\left)\right|\le \frac{1}{2}$
 $𝑦\prime -𝑦=\frac{1}{2}$
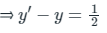
Now the solution of the differential equation is -
C.F. = C₁e^x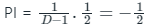
PI = $\frac{1}{𝐷}.\frac{1}{2}=-\frac{1}{2}$
Hence y = C1ex - 1/2
Now use the initial condition y(0) = -1 ⇒ C₁ = -1/2
⇒ y = -1/2 ex - 1/2
⇒ y = -1/2 ex < 0
⇒ y is monotone decreasing.
Now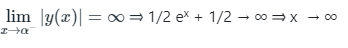  
but there does not exists an α ∈ (0, ∞)
Now as x → ∞ ,  y = -1/2 ex - 1/2 → - ∞ and y is decreasing as well.
So clearly it is not bounded below but it is bounded above.

Q3. Consider the initial value problem 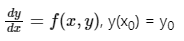. where f is a twice continuously differentiable function on a rectangle containing the point (x₀, y₀). With the step-size h, let the first iterate of a second order scheme to approximate the solution of the above initial value problem be given by
y₁ = y₀ + Pk₁ + Qk₂,
where k₁ = hf(x₀, y₀), k₂ = hf(x₀ + α₀h, y₀ + β₀k₁) and P, Q, α₀, β₀ ∈ ℝ.
Which of the following statements are correct?
Solution: the initial value problem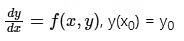

where f is a twice continuously differentiable function on a rectangle containing the point (x0, y0). With the step-size h, let the first iterate of a second order scheme to approximate the solution of the above initial value problem be given by
y1 = y0 + Pk1 + Qk2,
where k1 = hf(x0, y0), k2 = hf(x0 + α0h, y0 + β0k1) and P, Q, α0, β0 ∈ ℝ.
Compared with the Explicit Runge–Kutta method we get the relation,
P + Q = 1....(i)
Qα0 =1/2....(ii)
Qβ0 = 1/2....(iii)

Option (1): 
If α0 = 2, then by (ii) Q = 1/4
Then by (iii), β0 = 2
Hence by (i) P = 3/4
Therefore we get
If α0 = 2, then β0 = 2, $𝑃=\frac{3}{4},𝑄=\frac{1}{4}$
Option (1) is true, (3) is false

Option (2): 
If β0 = 2, then by (iii) Q = 1/6
Then by (ii), α0 = 3
Hence by (i) P = 5/6
Therefore we get
If β0 = 3, then α0 = 3, $𝑃=\frac{5}{6},𝑄=\frac{1}{6}$
Option (2) is true, (3) is false