Integer Answer Type Questions: Circle | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
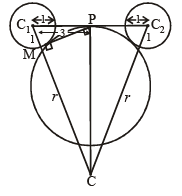
Q.1. The centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segement joining the centres of C1 and C2 and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C is
(2009)
Ans. (8)
Sol. Let r be the radius of required circle.
Clearly, in ΔC1CC2 , C1C = C2C =r+ 1
and P is mid point of C1C2
∴ CP ⊥ C1C2
Also PM ⊥ CC1
Now ΔPMC1 ~ΔCPC1 (by AA similarity)
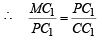
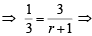 r + 1 = 9 ⇒ r = 8.
r + 1 = 9 ⇒ r = 8.
Q.2. The straight line 2x – 3y = 1 divides the circular region x2 + y2 ≤ 6 into two parts.
If 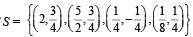 then the number ofpoints (s) in S lying inside the smaller part is (2011)
then the number ofpoints (s) in S lying inside the smaller part is (2011)
Ans. (2)
Sol.
The smaller region of circle is the region given by x2 + y2 < 6 ...(1)
and 2x – 3y > 1 ...(2)
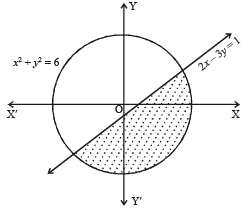
We observe that only two points 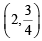 and
and 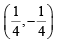
satisfy both the inequations (1) and (2)
∴ 2 points in S lie inside the smaller part.
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















