Integer Answer Type Questions: Conic Sections | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
1. The line 2x + y = 1 is tangent to the hyperbola 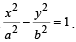
If this line passes through the point of intersection of the nearest directrix and the x-axis, then the eccentricity of the hyperbola is (2010)
Ans. (2)
Sol. Intersection point of nearest directrix x = 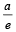 and x-axis
and x-axis
is 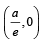
As 2x +y=1 passes through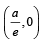
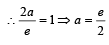
Also y = –2x+1 is a tangent to 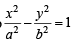
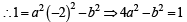
⇒ 4a2– a2e2 – 1=1 ⇒ 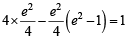
⇒ 4e2 –e4 +e2 = 4 ⇒ e4 – 5e4 + 4=0
⇒ e2 = 4 ase>1 for hyperbola. ⇒ e= 2
2. Consider the parabola y2 = 8x . Let Δ1 be the area of the triangle formed by the end points of its latus rectum and the point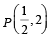 on the parabola and Δ2 be the area of the triangle formed by drawing tangents at P and at the end points of the latus rectum. Then
on the parabola and Δ2 be the area of the triangle formed by drawing tangents at P and at the end points of the latus rectum. Then 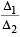 is (2011)
is (2011)
Ans. (2)
Sol. Δ1 = Area of ΔPLL' 
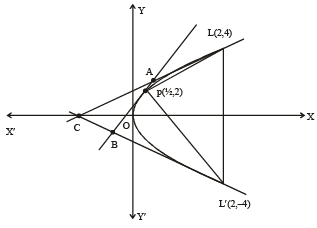
Equation of AB, y = 2x + 1 Equation of AC, y = x + 2 Equation of BC, – y = x + 2 Solving above equations we get A (1, 3), B (–1, –1), C (–2, 0)
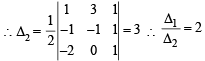
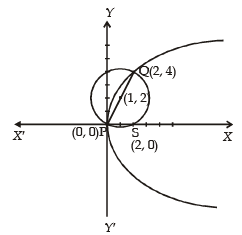
3. Let S be the focus of the parabola y2 = 8x and let PQ be the common chord of the circle x2 + y2 – 2x – 4y = 0 and the given parabola. The area of the triangle PQS is (2012)
Ans. (4)
Sol. We observe both parabola y2 = 8x and circle x2 + y2 – 2x – 4y = 0 pass through origin
∴ One end of common chord PQ is origin. Say P(0, 0)
Let Q be the point (2t2, 4t), then it will satisfy the equation of circle.
∴ 4t4 + 16t2 – 4t2 – 16t = 0 ⇒ t4 + 3t2 – 4t = 0 ⇒ t (t3 + 3t – 4) = 0
⇒ t (t – 1)(t2 + t – 4) = 0 ⇒ t = 0 or 1
For t = 0, we get point P, therefore t = 1 gives point Q as (2, 4).
We also observe here that P(0, 0) and Q(2, 4) are end points of diameter of the given circle and focus of the parabola is the point S(2, 0).
∴ Area of ΔPQS 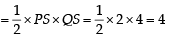 sq. units
sq. units
4. A vertical line passing through the point (h, 0) intersects the
ellipse 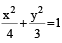
at the points P and Q. Let the tangents to the ellipse at P and Q meet at the point R. If Δ(h) = area of the triangle 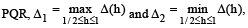 then
then
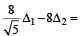 (JEE Adv. 2013)
(JEE Adv. 2013)
(a) g(x) is continuous but not differentiable at a
(b) g(x) is differentiable on R
(c) g(x) is continuous but not differentiable at b
(d) g(x) is continuous and differentiable at either (a) or (b) but not both
Ans. (9)
Sol. Vertical line x = h, meets the ellipse  at
at
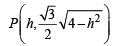 and
and 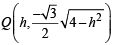
By symmetry, tangents at P and Q will meet each other at x-axis.
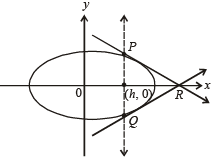
Tangent at P is 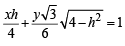
which meets x-axis at 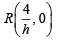
Area of ΔPQR = 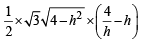
i.e.,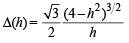
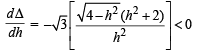
∴ Δ(h) is a decreasing function.
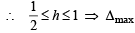

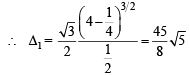
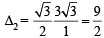
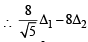 = 45 – 36 = 9
= 45 – 36 = 9
5. If the normals of the parabola y2 = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)2 + (y + 2)2 = r2, then the value of r2 is (JEE Adv. 2015)
Ans. (2)
Sol. End points of latus rectum of y2 = 4x are (1, +2)
Equation of normal to y2 = 4x at (1, 2) is y – 2 = –1(x – 1)
or x + y –3 = 0
As it is tangent to circle (x – 3)2 + (y + 2)2 = r2
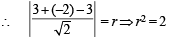
6. Let the curve C be the mirror image of the parabola y2 = 4x with respect to the line x + y + 4 = 0. If A and B are the points of intersection of C with the line y = –5, then the distance between A and B is (JEE Adv. 2015)
Ans. (4)
Sol. Let (t2, 2t) be any point on y2 = 4x. Let (h, k) be the image of (t2, 2t) in the line x + y + 4 = 0. Then
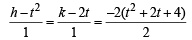
⇒ h = –(2t + 4) and k = –(t2 + 4)
For its intersection with, y = –5, we have –(t2 + 4) = –5 ⇒ t = +1
∴ A(–6, –5) and B(–2, –5) ∴ AB = 4.
7. Suppose that the foci of the ellipse
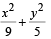 = 1 are (f1, 0)and (f2, 0) where f1 > 0 and f2 < 0. Let P1 and P2 be two parabolas with a common vertex at (0, 0) and with foci at (f1, 0) and (2f2, 0), respectively. Let T1 be a tangent to P1 which passes through (2f2, 0) and T2 be a tangent to P2 which passes through (f1, 0). If m1 is the slope of T1 and m2 is the slope of T2, then the value of
= 1 are (f1, 0)and (f2, 0) where f1 > 0 and f2 < 0. Let P1 and P2 be two parabolas with a common vertex at (0, 0) and with foci at (f1, 0) and (2f2, 0), respectively. Let T1 be a tangent to P1 which passes through (2f2, 0) and T2 be a tangent to P2 which passes through (f1, 0). If m1 is the slope of T1 and m2 is the slope of T2, then the value of
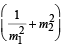 is (JEE Adv. 2015)
is (JEE Adv. 2015)
Ans. (4)
Sol. Ellipse :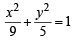
⇒ a = 3, b = 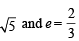
∴ f1 = 2 and f2 = –2 P1 : y2 = 8x and P2 : y2 = –16x
T1 : y = m1x +
It passes through (–4, 0),
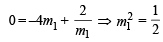
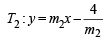
It passes through (2, 0)
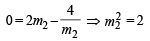
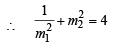
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Conic Sections - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What are conic sections? |  |
| 2. How are conic sections relevant to JEE Advanced? |  |
| 3. What is the general equation of a conic section? |  |
| 4. How can I determine the nature of a conic section from its equation? |  |
| 5. What are the properties of conic sections? |  |
















