Integer Answer Type Questions: Permutations and Combinations | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Consider the set of eight vectors 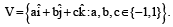 Three non- coplanar vectors can be chosen from V in 2p ways. Then p is (JEE Adv. 2013)
Three non- coplanar vectors can be chosen from V in 2p ways. Then p is (JEE Adv. 2013)
Ans. (5)
Sol. Given 8 vectors are (1, 1, 1), (–1, –1, –1); (–1, 1, 1), (1, –1, –1); (1, –1, 1),
(–1, 1, –1); (1, 1, –1), (–1, –1, 1)
These are 4 diagonals of a cube and their opposites.
For 3 non coplanar vectors first we select 3 groups of diagonals and its opposite in 4C3 ways.
Then one vector from each group can be selected in 2 × 2 × 2 ways.
∴ Total ways = 4C3 × 2 × 2× 2 = 32 = 25
∴ p = 5
Q.2. Let n1 < n2 < n3 < n4 < n5 be positive integers such that n1 + n2 + n3 + n4 + n5 = 20. Then the number of such distinct arrangements (n1, n2, n3, n4, n5) is (JEE Adv. 2014)
Ans. (7)
Sol. ∵ n1, n2, n3, n4 and n5 are positive integers such that n1 < n2 < n3 < n4 < n5
Then for n1 + n2 + n3 + n4 + n5 = 20 If n1, n2, n3, n4
take minimum values 1, 2, 3, 4 respectively then n5 will be maximum 10.
∴ Corresponding to n5 = 10,
there is only one solution n1 = 1, n2 = 2, n3 = 3, n4 = 4.
Corresponding to n5 = 9, we can have, only solution n1 = 1, n2 = 2, n3 = 3, n4 = 5 i.e., one solution
Corresponding to n5 = 8, we can have, only solution n1 = 1, n2 = 2, n3 = 3, n4 = 6 or n1 = 1, n2 = 2, n3 = 4, n4 = 4 i.e., 2 solution
For n5 = 7, we can have n1 = 1, n2 = 1, n3 = 4, n4 = 6 or n1 = 1, n2 = 3, n3 = 4, n4 = 5 i.e. 2 solutions
For n5 = 6, we can have n1 = 2, n2 = 3, n3 = 4, n4 = 5 i.e., one solution
Thus there can be 7 solutions.
Q.3. Let n ≥ 2 be an integer. Take n distinct points on a circle and join each pair of points by a line segment. Colour the line segment joining every pair of adjacent points by blue and the rest by red. If the number of red and blue line segments are equal, then the value of n is (JEE Adv. 2014)
Ans. (5)
Sol. Number of adjacent lines = n Number of non adjacent lines = nC2 – n
∴ nC2 – n = n ⇒  – 2n = 0
– 2n = 0
⇒ n2 - 5n=0 ⇒ n = 0 or 5
But n ≥ 2 ⇒ n = 5
Q.4. Let n be the number of ways in which 5 boys and 5 girls can stand in a queue in such a way that all the girls stand consecutively in the queue. Let m be the number of ways in which 5 boys and 5 girls can stand in a queue in such a way that exactly four girls stand consecutively in the queue.
Then the value of 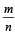 is (JEE Adv. 2015)
is (JEE Adv. 2015)
Ans. (5)
Sol. n = 5! × 6!
For second arrangement, 5 boys can be made to stand in a row in 5! ways, creating 6 alternate space for girls. A group of 4 girls can be selected in 5C4 ways. A group of 4 and single girl can be arranged at 2 places out of 6 in 6P2 ways. Also 4 girls can arrange themselves in 4! ways.
∴ m = 5! × 6P2 × 5C4 × 4!
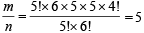
|
347 docs|185 tests
|
















