Integer Answer Type Questions: Ray & Wave Optics | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. The focal length of a thin biconvex lens is 20 cm. When an object is moved from a distance of 25 cm in front of it to 50 cm, the magnification of its image changes from m25 to m50. The ratio 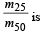 (2010)
(2010)
Ans. 6
Solution. 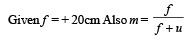
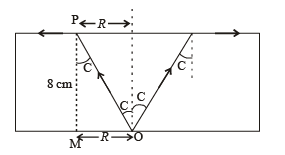
Q.2. A large glass slab (μ= 5 / 3) of thickness 8 cm is placed over a point source of light on a plane surface. It is seen that light emerges out of the top surface of the slab from a circular area of radius R cm. What is the value of R? (2010)
Ans. 6
Solution. In the figure, C represents the critical angle
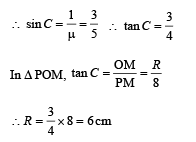
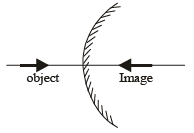
Q.3. Image of an object approaching a convex mirror of radius of curvature 20 m along its optical axis is observed to move from 25/3 m to 50/7 m in 30 seconds. What is the speed of the object in km per hour? (2010)
Ans. 3
Solution. Using mirror formula for first position
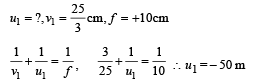
Using mirror formula for the second position
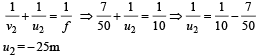
Change in position of object = 25 m
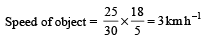
Q.4. Water (with refractive index = 4/3) in a tank is 18 cm deep. Oil of refractive index 7/4 lies on water making a convex surface of radius of curvature ‘R = 6 cm’ as shown. Consider oil to act as a thin lens. An object ‘S’ is placed 24 cm above water surface. The location of its image is at ‘x’ cm above the bottom of the tank. Then ‘x’ is (2011)
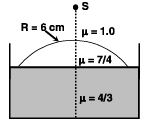
Ans. 2
Solution. For the convex spherical refracting surface of oil we apply
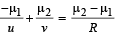
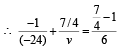
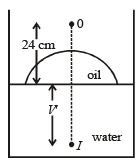
∴ v = 21 cm
For water-oil interface
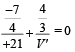
∴ V' = 16 cm.
This is the image distance from water-oil interface.
Therefore the distance of the image from the bottom of the tank is 2 cm.
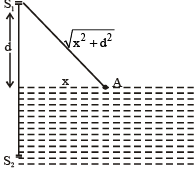
Q.5. A Young's double slit interference arrangement with slits S1 and S2 is immersed in water (refractive index = 4/3) as shown in the figure. The positions of maximum on the surface of water are given by x2 = p2m2λ2 – d2, where l is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an integer. The value of p is (JEE Adv. 2015)
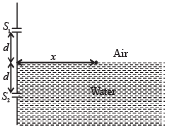
Ans. 3
Solution. For maxima
Path defference = mλ
∴ S2A – S1A = mλ
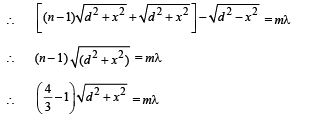
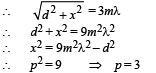
Q.6. Consider a concave mirror and a convex lens (refractive index = 1.5) of focal length 10 cm each, separated by a distance of 50 cm in air (refractive index = 1) as shown in the figure. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification M1. When the set-up is kept in a medium of refractive index 7/6, the magnification becomes M2. The magnitude  is (JEE Adv. 2015)
is (JEE Adv. 2015)
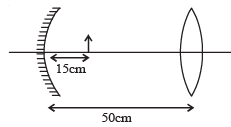
Ans. 7
Solution. Applying mirror formula
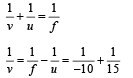
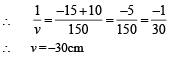

For convex lens u = |2fℓ|
Therefore image will have a magnification of 1.
When the set – up is kept in a medium
The focal length of the lens will change
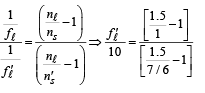
⇒ 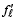 = 17.5 cm.
= 17.5 cm.
Applying lens formula 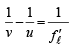
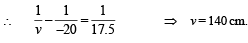
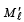 = Magnification by lens
= Magnification by lens 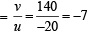
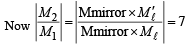
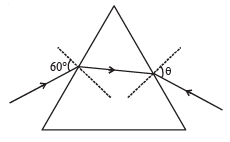
Q.7. The monochromatic beam of light is incident at 60° on one face of an equilateral prism of refractive index n and emerges from the opposite face making an angle θ(n) with the normal (see the figure). For n = √3 the value of q is 60° and 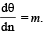
The value of m is (JEE Adv. 2015)
Ans. 2
Solution. Here ∠MPQ + ∠MQP = 60°. If ∠MPQ = r then ∠MQP
= 60 – r
Applying Snell’s law at P
sin60° = n sin r ...(i)
Differentiating w.r.t ‘n’ we get
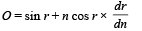 ...(ii)
...(ii)
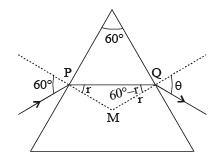
Applying Snell’s law at Q
sin θ = n sin (60° – r) ...(iii)
Differentiating the above equation w.r.t ‘n’ we get
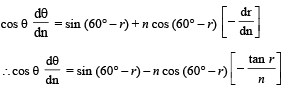
[from (ii)]
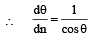 [sin (60° – r) + cos (60° – r) tan r] ...(iv)
[sin (60° – r) + cos (60° – r) tan r] ...(iv)
From eq. (i), substituting n = √3 we get r = 30°
From eq (iii), substituting n = √3 , r = 30° we get θ = 60°
On substituting the values of r and θ in eq (iv) we get
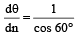 [sin 30° + cos 30° tan 30°] = 2
[sin 30° + cos 30° tan 30°] = 2
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Ray & Wave Optics - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is the difference between ray optics and wave optics? |  |
| 2. How does a lens form an image? |  |
| 3. What is the principle of superposition in wave optics? |  |
| 4. What is total internal reflection and its applications? |  |
| 5. What is the concept of polarization in wave optics? |  |
















