Integer Answer Type Questions: Trigonometric Functions & Equations | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. The number of all possible values of q where 0 < θ < π, for which the system of equations (y + z) cos 3θ = (xyz) sin 3θ
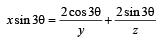
(xyz) sin 3θ = (y + 2z) cos 3θ + y sin 3θ
have a solution (x0, y0, z0) with y0 z0 ≠ 0, is (2010)
Ans. Sol. (3) The given equations are
xyz sin 3θ = ( y+ z ) cos3θ — (1)
xyz sin 3θ = 2 z cos3θ+ 2 y sin3θ — (2)
xyz sin3θ = y + 2z cos3θ+ y sin3θ — (3)
Operating (1) – (2) and (3) – (1), we get
(cos 3θ – 2 sinq )y – (cos 3θ)z = 0
and sin 3θ y + ( cos 3θ)z=0
which is homogeneous system of linear equation. But
y ≠ 0,z ≠ 0
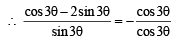 ⇒ cos 3θ = sin3θ
⇒ cos 3θ = sin3θ
⇒ 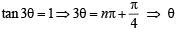 =
= 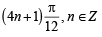
For θ ∈ (0,π) ⇒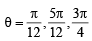
∴ Three such solutions are possible.
Q. 2. The number of values of q in the interval,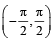 such that
such that 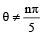 for n = 0, ±1,±2 and tanθ = cot 5θ as well as sin 2θ = cos 4θ is (2010)
for n = 0, ±1,±2 and tanθ = cot 5θ as well as sin 2θ = cos 4θ is (2010)
Ans. Sol. (3)

⇒ cos θ cos 5θ – sin5θ sinθ= 0 ⇒ cos 6θ=0
⇒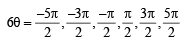
⇒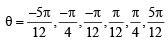
Again sin 2θ= cos 4θ= 1 – 2 sin 22θ
⇒ 2sin2 2θ + sin 2θ –1= 0 ⇒ sin 2θ = –1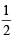
⇒ 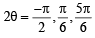
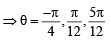
So common solutions are 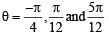
∴ Number of solutions = 3.
Q. 3. The maximum value of the expression
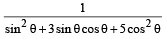
Ans. Sol. Let 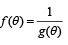
where g (θ) = sin 2θ+ 3 sinθ cos θ+ 5 cos2θ
Clearly f is maximum when g is minimum
Now (θ) = 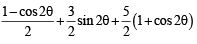
= 3 + 2cos 2θ + 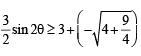
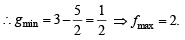
Q. 4. The positive integer value of n > 3 satisfying the equation
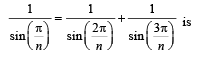 (2011)
(2011)
Ans. (7)
Sol. We have, 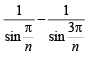
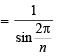
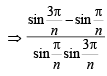
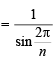
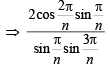
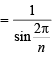
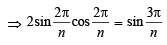
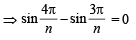
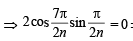

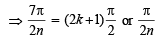 = 2kπ where k ∈ Z
= 2kπ where k ∈ Z
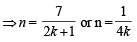
( n=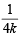 not possible for any integral value of k)
not possible for any integral value of k)
As n > 3, for k = 0, we get n = 7.
Q. 5. The number of distinct solutions of the equation
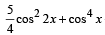
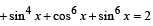 in the interval [0, 2π] is (JEE Adv. 2015)
in the interval [0, 2π] is (JEE Adv. 2015)
Ans. (8)
Sol. 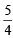 cos22x + cos4x + sin4x + cos6x + sin6x = 2
cos22x + cos4x + sin4x + cos6x + sin6x = 2
⇒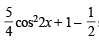
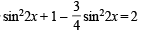
⇒  (cos22x – sin22x) = 0 ⇒ cos4x = 0
(cos22x – sin22x) = 0 ⇒ cos4x = 0
⇒ 4x = (2n + 1)  or x = (2n + 1)
or x = (2n + 1)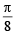
For x∈[0, 2π], n can take values 0 to 7
∴ 8 solutions.
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Trigonometric Functions & Equations - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What are the trigonometric functions commonly used in JEE Advanced? |  |
| 2. How do I solve trigonometric equations in JEE Advanced? |  |
| 3. Can trigonometric functions be negative in JEE Advanced? |  |
| 4. How can I find the values of trigonometric functions for special angles in JEE Advanced? |  |
| 5. What are the key properties of trigonometric functions in JEE Advanced? |  |





















