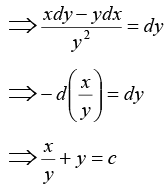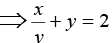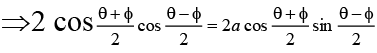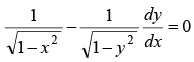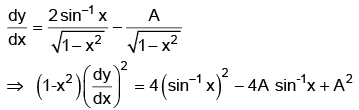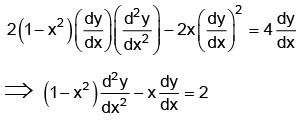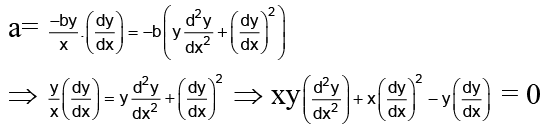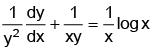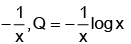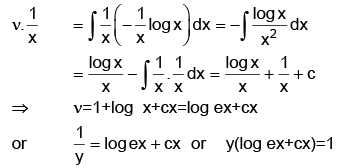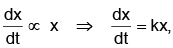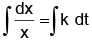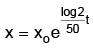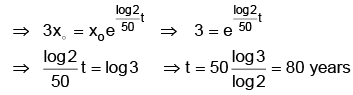Integer Answer Type Questions for JEE: Differential Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If xdy = y(dx + ydy), y > 0 and  y(1) = 1,  then y(-3) is equal to

Ans. 3

∵ y(1) = 1  ⇒ c = 2

⇒ y² -2y -3 = 0 ⇒ y = -1 or 3
⇒ y = 3   (∵ y > 0)

Q.2. The order of the differential equation of all tangent lines to the parabola y = x² is

Ans. 1
The parametric form of the given equation is x = t, y = t². The equation of any tangent at t is 2 xt = y + t². Differentiating, we get 2t = y₁`. Putting this value in the above equation, we have 2xy₁/2 = y + (y₁/2)² ⇒ 4xy₁ = 4y + y₁².  The order of this equation is one.

Q.3. The degree of the differential equation satisfying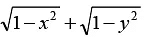= α(x - y) is

Ans. 1
Put x = sin θ, y = sin ϕ, so that given equation is reduced to 

cos θ + cos ϕ = a (sin θ - sin ϕ)

⇒ cot = (θ + ϕ)/2 = α ⇒ θ - ϕ = 2 cot^-1 a ⇒ sin^-1 x-sin^-1 y = 2 cot^-1 a.
Differentiating we get
So, the degree is one.

Q.4. The order of the differential equation of the family of circles with one diameter along the line y = x is 

Ans. 2
Centre of the circles can be taken as (a, a) and radius as r for some real numbers a and r. Thus, the family is a two parameter family. Hence, order of the corresponding differential equation is 2.

Q.5.  The order of the differential equation of all tangent lines to the parabola y = x² is

Ans. 1
The line x = my + 1/4m is tangent to the given parabola for all m. This line represents one parameter family of lines. Hence, the order of the corresponding differential equation is 1.

Q.6. The order of the differential equation whose general solution is given by
y= (C₁ + C₂) cos(X + C₃) – C_4e^X+C5 where C₁, C₂, C₃, C₄, C₅ are arbitrary constant is

Ans. 3
The given equation can be written as
y = Acos(x + C₃) - Be^x where A= C₁ + C₂ and B = C₄e^C₅
Hence, there are three independent variables, (A, B, C₃).
Thus, the order of the differential equation will be 3.

Q.7. Form the differential equation having y = (sin^-1x)² + A cos^-1x + B, where A and B are arbitrary constants, as its general solution.

Ans. 2
y = (sin^-1x)² + A cos^-1x +B  = (sin^-1x)² - A sin^-1x + πA/2 + B.
Differentiating w.r.t. x, we have

= 4y - 4B + A² - 2πA
Differentiating again w.r.t. x, we have

This is the required differential equation.

Q.8. Find the differential equation of all the conic whose axes coincide with the co-ordinate axis.

Ans. 0
Any conic whose axes coincides with co-ordinate axis is, ax² + by² =1
⇒ 2ax + 2by.dy/dx = 0
⇒ ax +  by dy/dx = 0  ...(i)
⇒ = 0 ……(ii)
From (i) and (ii),

Q.9. Solve (y logx - 1) ydx = xdy.

Ans. 1
The given differential equation can be written as
 . . . (1)
Divide by xy².  Hence

(3) is the standard linear differential equation with
P =
I.F = e^∫pdx = e^{∫-1/x dx} = 1/x
The solution is given by

Q.10. If the population of a country doubles in 50 years, in how many years will it triple under the assumption that the rate of increase is proportional to the number of inhabitants?

Ans. 80
Let x denote the population at a time t in years.
Then,
where k is a constant of proportionality.
Solving dx/dt = kx, we get
log x = kt + c ⇒ x = ekt+c ⇒ x = x₀e^kt ,
where x₀ is the population at time t = 0.

Since, it doubles in 50 years, at t = 50, we must have x = 2x₀.

Hence, 2x₀ = x₀e^50k ⇒ 50k = log 2
⇒ K = log2/50, so that
To  find t, when it triples i.e. x = 3x₀