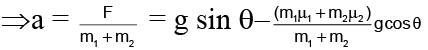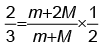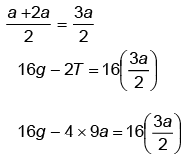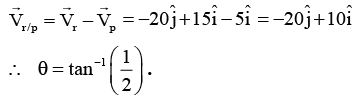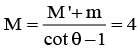Integer Answer Type Questions for JEE: Laws of Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The coefficient of static friction between a block of mass m and an incline is μs = 0.3. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane?
Ans. 16.7°
Angle of repose θ = tan-1(μ)
∴ θ = tan-1(0.3) = 16.7°
Q.2. The coefficient of static friction between a block of mass m and an incline is μs = 0.3. If the incline makes an angle of θ/2 with the horizontal, find the frictional force on the block.
Ans. 0.296 mg
Frictional force = μsmg cos (θ/2)
∴ ffr = 0.3 x cos (16.7/2)°mg = 0.296 mg
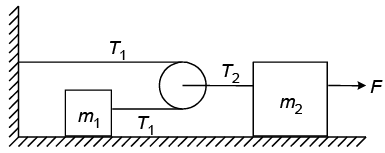
Q.3. In the figure shown, coefficient of friction between block A and ground is 0.4 and that between wedge and block B is zero. The wedge is fixed. Find the tension in the string and acceleration of block A if F = 28 N.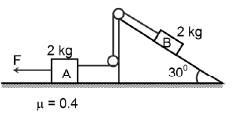
Ans. 15 N
fmax = μmg = 8 N
For block A:⇒ 28 - 8 - T = 2a . . . (1)
For block B:
T - mg sin 30° = ma
⇒ T -10 = 2a . . . (2)
From (1) and (2),
a = 2.5 m/s2 and T = 15 N
Q.4. Two blocks in contact and having masses 2 kg and 4 kg in succession from down to up are sliding down an inclined surface of inclination 30°. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and the incline is μ2. Calculate the acceleration of the 2.0 kg block if
(a) μ1 = 0.20 and μ2 = 0.30,
(b) μ1 = 0.30 and μ2 = 0.20. [Take g = 10 m/s2.]
Ans. 2.97 m/s2
Acceleration of a block sliding down an inclined plane is given by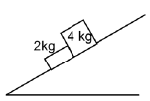
a = g ( -μ cos θ)
For 2 kg block, μ1 < μ2 , hence a1 > a2 Hence, the blocks move separately and with unequal accelerations.Acceleration of 2 kg block is a = g(sin 30 – 0.2 cos 30) = 10 (0.5 – 0.1732) = 3.27 m/s2
In case (B), when μ1 = 0.3 and μ2 = 0.2, the 2 kg block has less acceleration than the 3 kg block.
Thus, the blocks move together. When we draw the FBD and resolved the forces along the plane, we get F = (m1 + m2)g sin θ- (m1μ + m2μ2) g cos θ
= 10 sin 30°x 10 x cos 30° = 2.97 m/s2
Q.5. In the system shown below, friction and mass of the pulley are negligible. Find the acceleration of m2 if m1 = 300 g, m2 = 500 g and F = 3.4 N
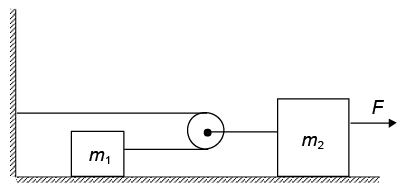
Ans. 2 m/s2
When the pulley moves a distance d, m1 will move a distance 2d. Hence m2 will have twice as large an acceleration as m2 has. Also because the total force on the pulley must be zero, T1 = (T2/2).
For mass m1, T1 = m1 (2a) … (i)
For mass m2, F – T2 = m2(A) … (ii)
Putting T1 = , (i) gives T2 = 4m1 a
Substituting in equation (ii), F = 4m1a + m2a = (4m1 + m2)a
Hence a == 2 m/s2
Q.6. A mass of 2 kg hangs freely at the end of a string, which passes over a smooth pulley fixed at the edge of a smooth table. The other end of the string is attached to a mass M on the table. If the mass on the table is doubled the tension in the string increases by one-half. Find the mass M.
Ans. 1 kg
The tension in the string is given by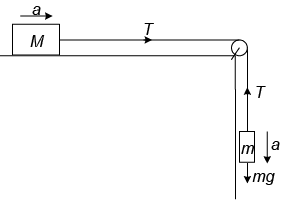
T =...(i)
In the second case M changes to 2M and T changes to 3/2 T… (ii)
Dividing (i) by (ii), we get
Substituting m = 2 kg, then
M = 1 kg
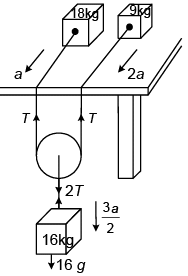
Q.7. Two particles of masses 9kg and 18 kg are placed on a smooth horizontal table. A string, which joins them, hangs over the edge supporting a light pulley, which carries a mass 16 kg. The two parts of the string on the table are parallel and perpendicular to the edge of the table. The parts of the string outside the table are vertical. Find the acceleration of the particle of mass 16kg. [ take g = 10 m/s2]
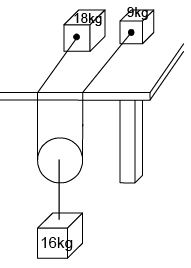
Ans. 4 m/s2
Let T be the tension in the string; a be the acceleration of the mass 18 kg; 2a be the acceleration of mass 9 kg.
T = m × 2a The mass 16 kg will come down with an acceleration
⇒ a = 8/3 m/s2
∴ the acceleration of 16 kg mass
= 3/2 a = 4 m/s2
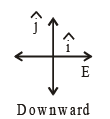
Q.8. Rain is falling vertically with a speed of 20 m/s. A person is running in the rain with a velocity of 5 m/s and a wind is also blowing with a speed of 15 m/s both from the west. The angle with the vertical at which the person should hold his umbrella so that he may not get drenched is tan-1(n/2). n =?
Ans. 1
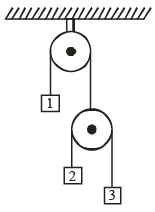
Q.9. At certain moment of time, velocities of 1 and 2 both are 1 m/s upwards. The velocity of 3 at that moment is x m/s downward. What is the value of x?
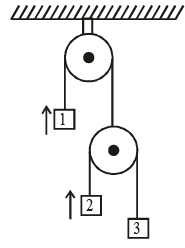
Ans. 3
α2 + α3 + 2α1 = 0
Similarly, we can findv2 + v3 + 2v1 = 0
Taking, upward direction as positive we are given
v1 = v2 = 1 m/s
∴ v3 = -3 m/s
i.e., velocity of blocks 3 is 3 m/s (downwards).
Q.10. Find the mass M (in kg) of the hanging block in figure which will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light. Take θ = 37°, M' = 1 kg , m = 1/3kg.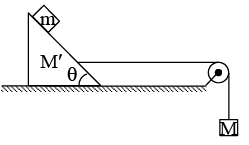
Ans. 4
For m to be at rest with respect to M', a = g tan θ
∴ T = (M'+ m) g tan θ
For block M, Mg - ( M '+ m) g tan θ = Mg tan θ
On solving,
|
446 docs|929 tests
|