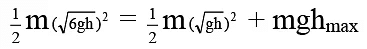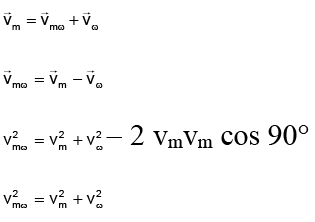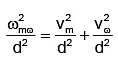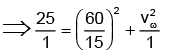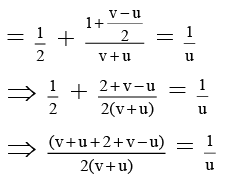Integer Answer Type Questions for JEE: Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A block is projected up on smooth inclined plane having angle of inclination 60º with speed √6gh . Maximum height (in meter) attained by block is -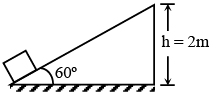

Ans. 2 sec.
At highest point velocity of block = √gh

⇒ h_max = 2.5 h = 5m

Q.2. A car accelerates from rest at a constant rate of 2 m/s² for some time. Then, its retards at a constant rate of 4 m/s² and comes to rest.  What is the maximum speed attained by the car  if it remains in motion for 3 seconds?

Ans. 4 m/s

v = a₁t₁ = a₂t₂

∴ t₁ = (a₂/a₁) t₂  = (4/2)t₂ = 2t₂.

Next, t₁ + t₂ = 3 or 2t₂ + t₂ = 3t₂ 
t₂ = 1 sec  and t₁ = 2 sec
∴ v = 2 x 2 = 4 m/s.

Q.3. A swimmer wishes to reach directly opposite bank of a river, flowing with velocity 8 m/s. The swimmer can swim 10 m/s in still water. The width of the river is 480 m. Time taken by him to do so is

Ans. 80s

Time taken
480/6 = 80s

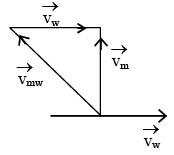
Q.4. A boat which has a speed of 5 km/hr in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water, in kilometer per hour, is

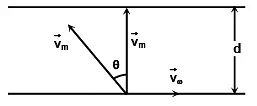
Ans. 3 km/hr

No  

⇒ v_ω = 3 km/hr

Q.5. Two particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively.  They collide in air and stick to each other.  The distance of the combined mass from point A is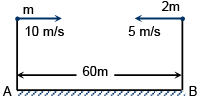

Ans. 80 m

They will fall through the same height say h. Let them collide at a distance x from tower A.
∴ h = 1/2 gt²    . . . (1)

x = 5t . . . (2)
60 - x = 10t . . . (3)
solving (2) and (3) we get x = 20 m, t = 4 sec, h = 80 m

Q.6. A constant retardation of 2.5 m/s² is applied to a body of mass 20 kg moving initially with a speed of 15 m/s.  How long does the body take to stop?

Ans. 6 sec

v = u -gt
t = u/g as v = 0
= 15/2.5 = 6 sec

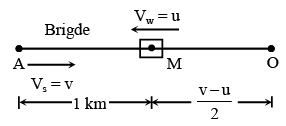
Q.7. A swimmer jumps from a bridge over a canal and swims 1 km up stream. After that first km, he passes a floating cork. He continues swimming for half an hour and then turns around and swims back to the bridge. The swimmer and the cork reach the bridge at the same time. The swimmer has been swimming at a constant speed. How fast does the water in the canal flow in km/hr.

Ans. 1
Let V_w = u & U_sw = v
Time taken by swimmer to go from M to O and O to B = time taken by float to reach B from M.


⇒ (2v + 2) u = 2(v + u)
⇒ 2vu + 2u = 2v + 2u
u = 1 km/hr

Q.8. Figure shows the graph of the x-co-ordinate of a particle going along the x-axis as function of time. Find the instantaneous speed of particle at t = 12.5 s (in m/s)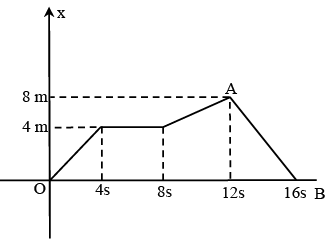

Ans. 2
B = 2m/s
Slope of line AB = – 2m/s
Speed of particle at t = 12.5 s
v = 2m/s

Q.9. Figure shows the graph of velocity versus time for a particle going along x axis. Initially at t = 0, particle is at x = 3m. Find position of particle at t = 2s. (in m)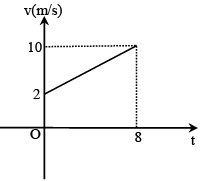

Ans. 9
v = t + 2
v₂ = 4 m/s, at t₂ = s.
x₂ – x₀ = 1/2 × (2 + 4) × 2
= 6m
x₂ = 9m

 Q.10. A police jeep is chasing a culprit going on a motor bike. The motor bike crosses a turning at a speed of 72 km/h. The jeep follows it a speed of 90 km/h crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike? (in km)

Ans. 1
Speed of bike = 72 × 5/18 = 20 m/s

Speed of jeep = 90 × 5/18 = 25 m/s.
Relative velocity of jeep w. r. t. bike = 25 – 20 = 5 m/s
Distance covered by bike in 10s = 20 × 10 = 200 m.
Time taken by Jeep to cover 200 m with velocity 5 m/s. t = 200/5 = 40 s.
Therefore distance covered by police jeep in 40 s = 40 × 25 = 1000 m = 1 km.