Integral Calculus | Quantitative Aptitude for CA Foundation PDF Download
INTEGRAL CALCULUS
INTEGRATION
Integration is the reverse process of differentiation.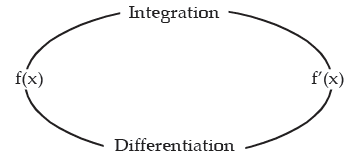
We know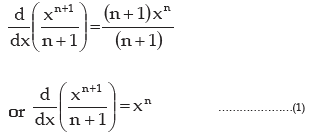
Integration is the inverse operation of differentiation and is denoted by the symbol .
Hence, from equation (1), it follows that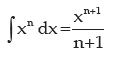
i.e. Integral of xn with respect to variable x is equal to 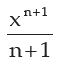
Thus if we differentiate 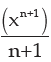 we can get back xn.
we can get back xn.
Again if we differentiate 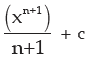 and c being a constant, we get back the same xn
and c being a constant, we get back the same xn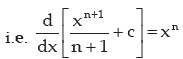
Hence 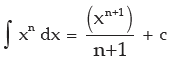 and this c is called the constant of integration
and this c is called the constant of integration
Integral calculus was primarily invented to determine the area bounded by the curves dividing the entire area into infinite number of infinitesimal small areas and taking the sum of all these small areas.
BASIC FORMULAS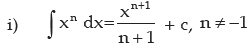
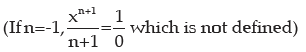
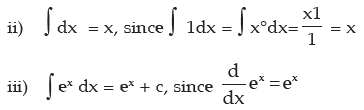
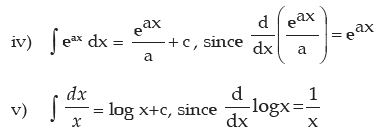
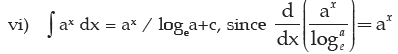
Note: In the answer for all integral sums we add +c (constant of integration) since the differentiation of constant is always zero.
Elementary Rules: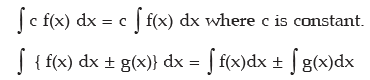
Examples :
Find
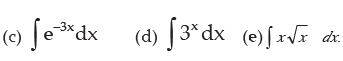
Solution: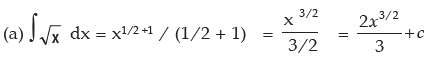
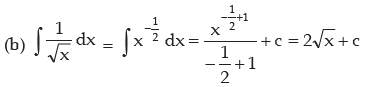 where c is arbitrary constant
where c is arbitrary constant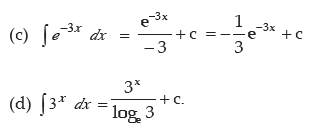
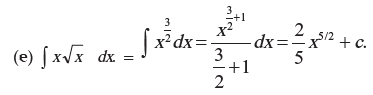
Examples: Evaluate the following integral: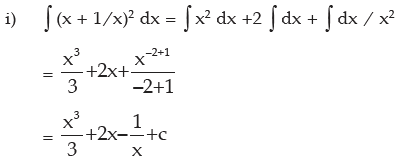
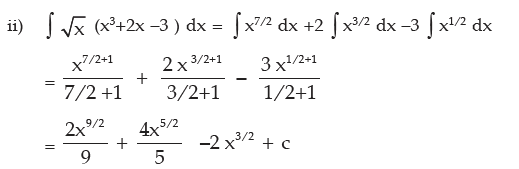
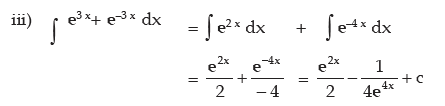
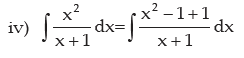
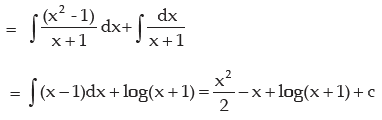
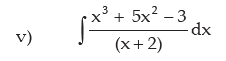

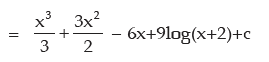
METHOD OF SUBSTITUTION (CHANGE OF VARIABLE)
It is sometime possible by a change of independent variable to transform a function into another which can be readily integrated.
We can show the following rules.
To put z = f (x) and also adjust dz = f'(x) dx
Example: ∫F{ h(x )} h'(x ) dx, take ez = h(x) and to adjust dz = h'(x) dx
then integrate F(z) d using normal rule.
Example: 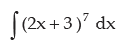
We put (2x + 3) = t ⇒ so 2 dx = dt or dx = dt / 2
Therefore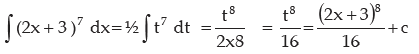
This method is known as Method of Substitution
Example: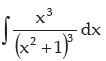
We put (x2 +1) = t
so 2x dx = dt or x dx = dt / 2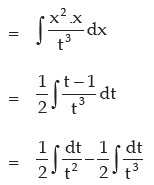
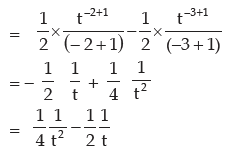
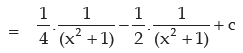
IMPORTANT STANDARD FORMULAE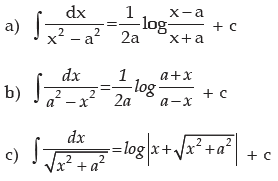
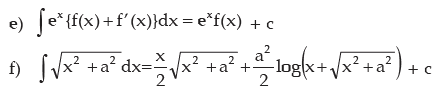
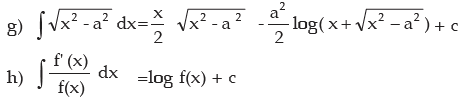
Examples: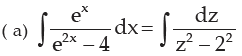 where z=ex dz = ex dx
where z=ex dz = ex dx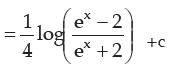
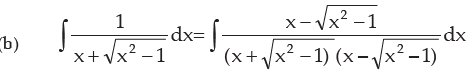
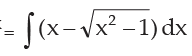
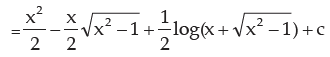
INTEGRATION BY PARTS
where u and v are two different functions of x
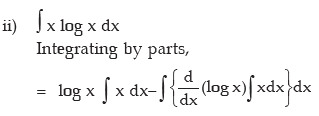
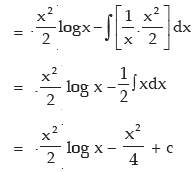
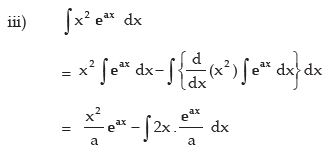
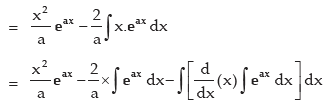
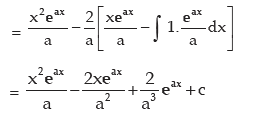
METHOD OF PARTIAL FRACTION
Type I: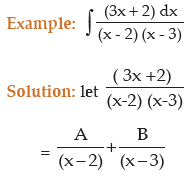
[Here degree of the numerator must be lower than that of the denominator; the denominator contains non–repeated linear factor]
so 3x + 2 = A (x – 3) + B (x – 2)
We put x = 2 and get
3.2 + 2 = A (2–3) + B (2–2) => A = –8
we put x = 3 and get
3.3 +2 = A (3–3) + B (3–2) => B= 11
Type II:
Example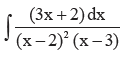
Solution: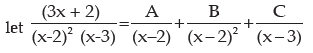
or 3x + 2 = A (x – 2) (x – 3) + B (x – 3) +C (x – 2)2
Comparing coefficients of x2, x and the constant terms of both sides, we find
A+C = 0 …………(i)
–5A + B – 4C = 3 ……(ii)
6A – 3B + 4C = 2 …….(iii)
By (ii) + (iii) A – 2B = 5 ..…….(iv)
(i) – (iv) 2B + C = –5 …….(v)
From (iv) A = 5 + 2B
From (v) C = –5 – 2B
From (ii) –5 ( 5 + 2B) + B – 4 (– 5 – 2B) = 3
or – 25 – 10B + B + 20 + 8B = 3
or – B – 5 = 3
or B = – 8, A = 5 – 16 = – 11, from (iv) C = – A = 11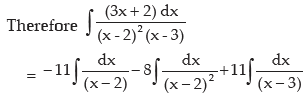
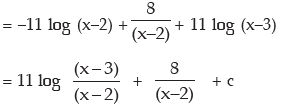
Type III:
so 3x2 –2x +5 = A (x2 + 5 ) + (Bx +C) (x–1)
Equating the coefficients of x2, x and the constant terms from both sides we get
A + B = 3 …………(i)
C – B = –2 …………(ii)
5A – C = 5 ………….(iii)
by (i) + (ii) A + C = 1 ……… (iv)
by (iii) + (iv) 6A = 6 ……… (v)
or A = 1
therefore B = 3 – 1 = 2 and C = 0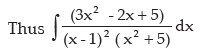
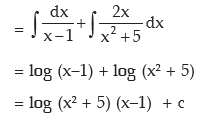
Example: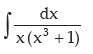
Solution: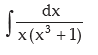
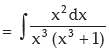 we put x3 = z, 3x2 dx = dz
we put x3 = z, 3x2 dx = dz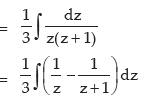
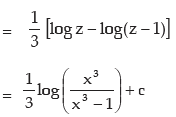
Example: Find the equation of the curve where slope at (x, y) is 9x and which passes through the origin.
Solution:
Since it passes through the origin, c = 0; thus required eqn . is 9x2 = 2y.
DEFINITE INTEGRATION
Suppose F(x) dx = f (x)
As x changes from a to b the value of the integral changes from f (a) to f (b). This is as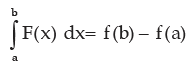
‘b’ is called the upper limit and ‘a’ the lower limit of integration. We shall first deal with
indefinite integral and then take up definite integral.
Example: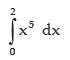
Solution: 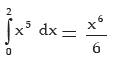
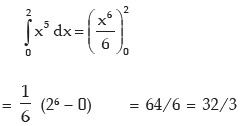
Note: In definite integration the constant (c) should not be added
Example: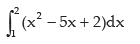
Solution: 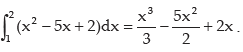
Now,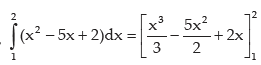
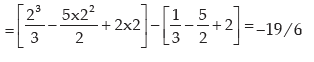
IMPORTANT PROPERTIES
Important Properties of definite Integral
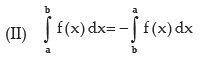
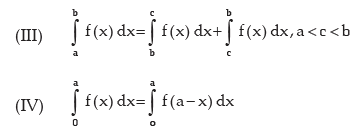
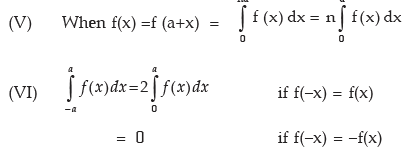
Example: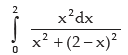
Solution: 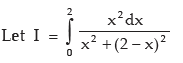
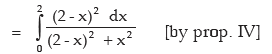
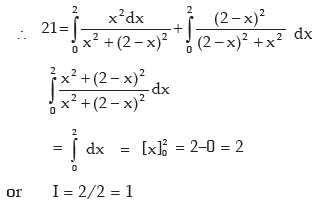
Example: Evaluate 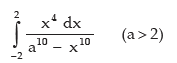
Solution: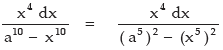
let x5 = t so that 5x4 dx = dt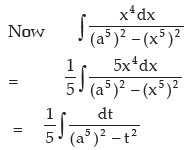
 (by standard formula b)
(by standard formula b)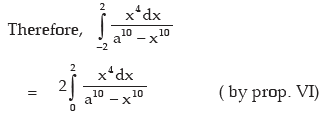
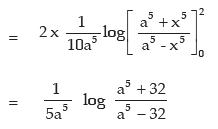
|
101 videos|209 docs|89 tests
|
FAQs on Integral Calculus - Quantitative Aptitude for CA Foundation
| 1. What is integral calculus? |  |
| 2. How is integral calculus different from differential calculus? |  |
| 3. What are the applications of integral calculus in real life? |  |
| 4. How do you evaluate definite integrals? |  |
| 5. What are some common techniques used in integral calculus? |  |






















