Internally constraint materials
Till now we have been focusing on materials that have no internal constraint, that is, if the required body force and boundary traction can be applied, any
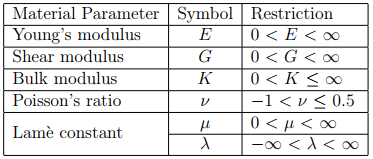
Table 6.1: Restrictions on material parameters
smooth displacement field can be realized in bodies made of these materials. However, in some materials this is not true. Only smooth displacement fields that satisfy certain constraints are realizable. The most common constraint on the displacement field is that it be volume preserving. Contrary to the reality, beginners tend to think that in all materials volume is preserved in all feasible deformations just because the cross sectional area reduces when uniaxially stretched. However, this is not true. We show this next. Recollecting from chapter 3 (section 3.6) that the ratio of the deformed volume, v to the original volume, V in case of homogeneous deformation is given by,
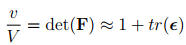 (6.95)
(6.95)
where we have used equation (6.70c) to approximately compute det(F) when the components of the displacement gradient are small. Using equation (6.77) that gives the state of strain in the cuboid subjected to uniaxial stress, σa, the change in its volume is computed to be
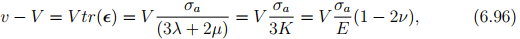
where the last two equalities are obtained using equation (6.90) and (6.91). Thus, it is apparent that the volume of the cuboid changes as the magnitude of the uniaxial stress changes when ν ≠ 0.5. For physically possible values of Poisson’s ratio, other than 0.5, the volume increases when uniaxially stretched and decreases when compressed.
In this section, we outline general principle to generate constitutive relations for internally constrained materials. Assuming that the materials internal constraint can be given by a equation of the form,
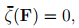 (6.97)
(6.97)
where  is a scalar valued function. The requirement that the internal constraint (6.97) be objective necessitates
is a scalar valued function. The requirement that the internal constraint (6.97) be objective necessitates
 (6.98)
(6.98)
For (6.98) to hold:
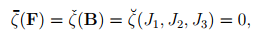 (6.99)
(6.99)
where Ji are the invariants of B as defined in (6.33). The proof for this is left as an exercise; the steps leading to this is similar to that used to obtain the constitutive representation for Cauchy stress.
In order to accommodate its motion to an internal constraint a material body must be able to bring appropriate contact forces into play and the constitutive equation governing its stress response must be such as to allow these forces to act. Thus, the stress at a point x and time t is uniquely determined by the value of the deformation gradient to within a symmetric tensor A which is not determined by the motion of the body and which does no work in any motion compatible with the constraints, i.e.,
σ = α01 + α1B + α2B−1 + A, (6.100)
where 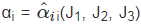 are the same material response functions as defined before in (6.32) and Ji ’s are invariants of B defined in (6.33).
are the same material response functions as defined before in (6.32) and Ji ’s are invariants of B defined in (6.33).
It can be shown that15, the rate at which the applied stresses does work is given by the expression σ � l, where l = grad(v), the Eulerian gradient of the velocity field. Hence, the requirement that A do no work requires that
A � l = 0, (6.101)
| 15Derivation of this can be found in standard text books in continuum mechanics like [1, 2]. For understanding these derivation a lot more concepts needs to be grasped which is beyond the scope of this course. In fact, the following derivation here is also not easy to follow; but made as simple as possible. To proceed further in this course, it suffices to understand that there is a formal procedure to obtain constitutive relations for materials with constraints. |
for all allowable motions. To relate A with 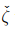 we take material time derivative of (6.99) to obtain
we take material time derivative of (6.99) to obtain
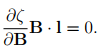 (6.102)
(6.102)
Now let
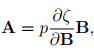 (6.103)
(6.103)
where p is an arbitrary scalar to be determined from boundary conditions and/or equilibrium equations. While it is easy to show that, the above choice for the constraint stress satisfies the requirement (6.101), it is difficult to show that this is the only choice and is beyond the scope of this course.
Hence, a general representation for stress with kinematic constraint (6.99) is given by
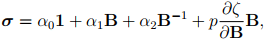 (6.104)
(6.104)
with a undetermined scalar p to be found using equilibrium equations and/or boundary conditions.
Incompressible materials
As already discussed, material that can undergo only isochoric motions is called incompressible material. As was shown in chapter - 3 for isochoric motions, det(F) = J3 = 1. Hence,
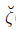 (J1, J2, J3) = J3 − 1 = 0. (6.105)
(J1, J2, J3) = J3 − 1 = 0. (6.105)
Substituting (6.105) in (6.103) and using (2.189) we obtain
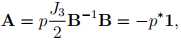 (6.106)
(6.106)
where p* = −p/2. Consequently, a general representation for Cauchy stress (6.104) for incompressibility constraint reduces to,
σ = (α0 − p* )1 + α1B + α2B−1 , (6.107)
where now, αi = 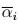 (J1, J2) since J3 is identically 1. Now introducing, p+ = −α0 + p* , we obtain
(J1, J2) since J3 is identically 1. Now introducing, p+ = −α0 + p* , we obtain
σ = −p+1 + α1B + α2B−1 , (6.108)
where without any loss of generality we assume p+ to be some arbitrary scalar to be determined from boundary conditions and/or equilibrium equations. For convenience and brevity in notation we shall drop the superscript + in p+ and write
σ = −p1 + α1B + α2B−1 , (6.109)
which we consider as the most general representation for Cauchy stress in an incompressible material being subjected to elastic deformation.
As before (see section 6.4), it can be shown that when the components of the displacement gradient is small, the kinematical constraint equation (6.105) reduces to requiring,
tr(∈) = 0, (6.110)
and consequently the equation (6.109) can be approximated as,
σ = −p1 + 2�inc∈, (6.111)
where �inc is a constant material parameter and p is an arbitrary scalar to be determined from equilibrium equations and/or boundary condition. Equation (6.111) is the constitutive relation for an incompressible material undergoing elastic deformation such that the components of the displacement gradient are small.
Before concluding this section, we would like to find the value of all the material parameters defined in section 6.5 for this incompressible material. In case of the cuboid being subjected to uniaxial stress, the state of stress and strain are:
 (6.112)
(6.112)
The incompressibility condition (6.110) requires that
∈1 + 2∈2 = 0. (6.113)
Hence, the incompressible materials Poisson’s ratio,
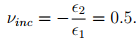 (6.114)
(6.114)
Substituting (6.112) along with the requirement that ∈2 = −∈1/2 obtained from (6.113) for stress and strain in (6.111) we obtain:
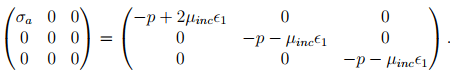 (6.115)
(6.115)
For the above equation to hold, p = −�inc∈1 and hence, σa = 3�inc∈1. Thus, the incompressible materials Young’s modulus,
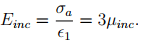 (6.116)
(6.116)
If the cuboid is being subjected to pure shear state of stress and strain,
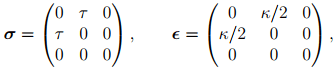 (6.117)
(6.117)
then it is straightforward to verify that for this state of strain tr(∈) = 0 and therefore the incompressibility condition (6.110) is met. Substituting, (6.117) in (6.111) we obtain:
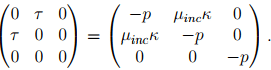 (6.118)
(6.118)
For this equation to hold, p = 0 and τ = �incκ. Now, the incompressible shear modulus is,
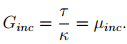 (6.119)
(6.119)
Finally, if a incompressible cuboid is subjected to hydrostatic pressure, σ = −p1 and ∈ = 0, for the incompressibility constraint (6.110) and the constitutive relation (6.111) to hold. Thus, incompressible materials bulk modulus, Kinc = ∞.
Understandably there is only one material parameter in (6.111). The incompressibility constraint (6.110) requires that νinc = 0.5 or equivalently, Kinc = ∞ there by fixing one of the two independent material parameters in the isotropic Hooke’s law.
As you would have noticed, for incompressible materials, both the state of stress and strain are prescribed and found necessary to solve certain boundary value problems. On the other hand for unconstrained materials only stress (or strain) needs to be specified for the same boundary value problems. Hence, the solution techniques used for solving unconstrained materials is different from that of constrained materials. In the remainder of this course we focus on the unconstrained materials.
(6.95)
(6.97)
is a scalar valued function. The requirement that the internal constraint (6.97) be objective necessitates
(6.98)
(6.99)
are the same material response functions as defined before in (6.32) and Ji ’s are invariants of B defined in (6.33).
we take material time derivative of (6.99) to obtain
(6.102)
(6.103)
(6.104)
(J1, J2, J3) = J3 − 1 = 0. (6.105)
(6.106)
(J1, J2) since J3 is identically 1. Now introducing, p+ = −α0 + p* , we obtain
(6.112)
(6.114)
(6.115)
(6.116)
(6.117)
(6.118)
(6.119)



















