Introduction: Applications of Viscous Flows Through Pipes - 2 | Fluid Mechanics for Mechanical Engineering PDF Download
Concept of Flow Potential and Flow Resistance
- Consider the flow of water from one reservoir to another as shown in Fig. 35.3. The two reservoirs A and B are maintained with constant levels of water. The difference between these two levels is
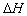 as shown in the figure. Therefore water flows from reservoir A to reservoir B .
as shown in the figure. Therefore water flows from reservoir A to reservoir B .
- Application of Bernoulli's equation between two points A and B at the free surfaces in the two reservoirs gives
where hf is the loss of head in the course of flow from A to B .
- Therefore, Eq. (35.10) states that under steady state, the head causing flow Δ H becomes equal to the total loss of head due to the flow.
- Considering the possible hydrodynamic losses, the total loss of head hf can be written in terms of its different components as
35.11
Loss of heat at Friction loss in Exit loss to the
entry to the pipe pipe over its reservoir B
from reservoir A length L
where, V is the average velocity of flow in the pipe.
(contd from previous...) Concept of Flow Potential and Flow Resistance
The velocity V in the above equation is usually substituted in terms of flow rate Q , since, under steady state, the flow rate remains constant throughout the pipe even if its diameter changes. Therefore, replacing V in Eq. (35.11) as we finally get
(35.12)
(35.13)
The term R is defined as the flow resistance .
In a situation where f becomes independent of Re, the flow resistance expressed by Eg. (35.13) becomes simply a function of the pipe geometry. With the help of Eq. (35.10), Eq. (35.12) can be written as
( 35.14)
ΔH in Eq. (35.14) is the head causing the flow and is defined as the difference in flow potentials between A and B.
This equation is comparable to the voltage-current relationship in a purely resistive electrical circuit. In a purely resistive electrical circuit, ΔV = Rl, where ΔVis the voltage or electrical potential difference across a resistor whose resistance is R and the electrical current flowing through it is I.
- The difference however is that while the voltage drop in an electrical circuit is linearly proportional to current, the difference in the flow potential in a fluid circuit is proportional to the square of the flow rate.
- Therefore, the fluid flow system as shown in Fig. 35.3 and described by Eq. (35.14) can be expressed by an equivalent electrical network system as shown in Fig. 35.4.
Fig 35.4 Equivalent electrical network system for a simple pipe flow problem shown in Fig.35.3
|
56 videos|146 docs|75 tests
|
FAQs on Introduction: Applications of Viscous Flows Through Pipes - 2 - Fluid Mechanics for Mechanical Engineering
| 1. What are some common applications of viscous flows through pipes? |  |
| 2. How is the flow rate affected by the viscosity of the fluid? |  |
| 3. What is the Reynolds number and how does it relate to viscous flows through pipes? |  |
| 4. How does pipe diameter affect viscous flows? |  |
| 5. What factors can cause an increase in the pressure drop in viscous flows through pipes? |  |
















