Introduction & Examples: Number Series | General Intelligence and Reasoning for SSC CGL PDF Download
What is Number Series?
A series is an informally speaking of numbers. It is the sum of the terms of a sequence. Finite terms and series are defined by first and last terms while infinite series is endless.
- Number series is a form of series in which particular numbers are present in a particular order and missing numbers are to find out, nowadays number series is an important part of each and every government exams, especially in banks. It acquires a high weight.
- A series is solved by particular number series tricks, formulas, attitudes of a person. There are various types of series present in the exam. Series can be of many types of Numbers like Natural numbers, Whole numbers, Contagious numbers etc. A sequence is described as a list of elements with a particular order.
Types of Number Series
There are multiple types of number series available:
(i) Integer Number Sequences: There are particular formulas tricks to solve number series. Each number series question is solved in a particular manner. This series is the sequence of real numbers decimals and fractions. Number series example of this is like 1, 3, 5, 9….. etc. in which what should come next in Solved by number series shortcuts tricks performed by the candidate.
(ii) Rational Number Sequences: These are the numbers which can be written as a fraction or quotient where numerator and denominator both consist of integers. An example of this series is ½, ¾, 1.75 and 3.25.
(iii) Arithmetic Sequences: It is a mathematical sequence which consisting of a sequence in which the next term originates by adding a constant to its predecessor. It is solved by a particular formula given by the mathematics Xn = x1 + (n – 1)d. An example of this series is 3, 8, 13, 18, 23, 28, 33, 38, in which number 5 is added to its next number.
(iv) Geometric Sequences: It is a sequence consisting of a multiplying so as to group in which the following term starts the predecessor with a constant. The formula for this series is Xn= x1 rn-1. An example of this type of number sequence could be the following: 2, 4, 8, 16, 32, 64, 128, 256, in which multiples of 2 are there.
(v) Square Numbers: These are also known as perfect squares in which an integer is the product of that integer with itself. Formula= Xn= n2. An example of this type of number sequence could be the following: 1, 4, 9, 16, 25, 36, 49, 64, 81, ..
(vi) Cube Numbers: Same as square numbers but in these types of series an integer is the product of that integer by multiplying 3 times. Formula= Xn=n3. Example:- 1, 8, 27, 64, 125, 216, 343, 512, 729, …
(vii) Fibonacci Series: A sequence consisting of a sequence in which the next term originates by addition of the previous two Formula = F0 = 0 , F1 = 1, Fn = Fn-1 + Fn-2. An example of this type of number sequence could be the following: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Shortcuts – Tricks for Number Series
Number Series puzzles can be solved by various tricks provided by mathematics.
Firstly check the direct formulas as in like check:
(i) if all the numbers are prime, even or odd.
(ii) If all the numbers are perfect squares or cubes.
(iii) If all the numbers have a particular divisibility.
(iv) If all the numbers are succeeding by some additions or subtraction or multiplications or divisions by a particular number or addition of their cubes and squares. Number series methods are teaches by a professional to a student so that number series can be solved quickly and correctly. Now comes the Number series questions for IBPS Exam.
1. How to Solve Number Series Problem?
Ans. As talked about over the number series problems are solved by some particular number series rules applied logically.There are various methods to solve number series like predict the next number ii.e which number will come next by applying rules like by adding, subtracting etc. or by applying various shortcut tricks.
2. What Types of questions asked in bank exams related to number series?
Ans. There are various types of questions asked in bank exams.
Type I
In this kind of inquiries, a series of numbers is given with one number missing represented by a question mark. The Candidate has to select from the options available to correct option in place of the question mark.
The given sequences of numbers will be such that every number takes after its predecessor in the same way, i.e., according to a particular pattern. Hopefuls are required to figure out the right ways in which the sequence is formed and thereafter find out the number to finish the arrangement.
Example 1.
(i) 30, 34, 43, 59, 84, 120,?
(a) 169
(b) 148
(c) 153
(d) 176
(e) None of these
Ans. (a)
Solution.
The series follows the pattern of +4, +9, +16, +25 and so on.
So, at the end, 120 + 49 = 169
(ii) 40, 54, 82, ?, 180, 250
(a) 142
(b) 124
(c) 136
(d) 163
(e) None of these
Ans. (b)
Solution.
Let the missing number be P.
The given series 40, 54, 82, P, 180, 250.
Let’s observe the relation between numbers in the series. The numbers are in increasing order. So 82 < P < 180.
Difference between first number and second number is 54 – 40 = 14
Difference between second number and third number is 82 – 54 = 28
Difference between the third and fourth numbers is P – 82.
Difference between fourth and fifth numbers is 180 – P.
Difference between the last two numbers of the series is 250 – 180 = 70.
If we observe these differences they are multiples of 14.
The first difference is 14.
The second difference is 14 × 2 = 28.
The fifth difference is 14 x 5 = 70
⇒ The third difference will be P − 82 = 14 × 3
⇒ P − 82 = 42
⇒ P = 42 + 82
∴ The missing value is P = 124.
(iii) 222, 350, 520, ?
(a) 728
(b) 729
(c) 738
(d) 741
(e) None of these
Ans. (c)
Solution. We have the terms of this series formed in the following manner
⇒ 222 = 63 + 6
⇒ 350 = 73 + 7
⇒ 520 = 83 + 8
⇒ ? = 93 + 9
⇒ ? = 729 + 9
⇒ ? = 738
(iv) 1, 3, 7, 15, 31, ?
(a) 63
(b) 64
(c) 53
(d) 74
(e) None of these
Ans. (a)
Solution. We have the terms of the given series as
⇒ 21 – 1 = 1
⇒ 22 – 1 = 3
⇒ 23 – 1 = 7
⇒ 24 – 1 = 15
⇒ 25 – 1 = 31
⇒ ? = 26 – 1 = 63
Type II
In this we are given a sequence of number. The whole sequence, except the odd number, follow a certain rule. You need to search that number which does not follow the rule.
Example 2.
(i) 0, 1, 3, 8, 18, 35, 264
(a) 62
(b) 35
(c) 18
(d) 8
(e) None of these
Ans. (a)
Solution.
The pattern is +(02 + 1), + (12 + 1), + (22 + 1), + (32 + 1), + (42 + 1), +(52 + 1)
So, 264 is wrong and must be replaced by 35 + (52 + 1) = 62
(ii) 1, 9, 125, 49, 729, 121, 2147
(a) 2147
(b) 729
(c) 125
(d) 1
(e) None of these
Ans. (a)
Solution.
13 = 1
32 = 9
53 = 125
72 = 49
93 = 729
112 = 121
133 = 2197
So the odd one is 149 and 2147.
(iii) 1050, 510, 242, 106, 46, 16, 3
(a) 510
(b) 242
(c) 106
(d) 46
(e) None of these
Ans. (c)
Solution. (1050 – 30)/2 = 510
(510 – 26)/2 = 242
(242 – 22)/2 = 110
(110 – 18)/2 = 46
(46 – 14)/2 = 16
(16 – 10)/2 = 3
∴ 110 should be there in place of 106.
Some of the questions asked in Number Series Previous Papers
Directions: In each of these questions a number series is given. In each series stand-out number isn’t right. Discover the wrong number. (IBPS CWE PO/MT Exam 2012)
Question: 5531, 5506, 5425, 5304, 5135, 4910, 4621
(a) 5531
(b) 5425
(c) 4621
(d) 5135
(e) 5506
Ans. (a)
Solution.
5531 - 52 = 5506
5506 - 92 = 5425
5425 - 112 = 5304
5134 - 132 = 5135
5135 - 152 = 4910
4910 - 172 = 4621
Ever number after 5531 has a difference of a square.
Hence 5531 is the wrong number.
(ii) 6, 7, 9, 13, 26, 37, 69
(a) 7
(b) 26
(c) 69
(d) 37
(e) 9
Ans. (b)
Solution. 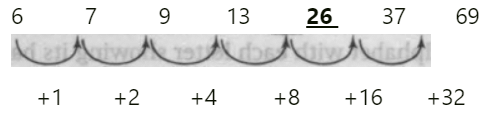
The number should be 21 in place of 26.
(iii) 1, 3, 10, 36, 152, 760, 4632
(a) 3
(b) 36
(c) 4632
(d) 760
(e) 152
Ans. (d)
Solution.
(1 x 1) + 2 = 3
(3 x 2) + 4 = 10
(10 x 3) + 6 = 36
(36 x 4) + 8 = 152
(152 x 5) + 10 = 770
(770 x 6) + 12 = 4632
Therefore wrong term 760
(iv) 4, 3, 9, 34, 96, 219, 435
(a) 4
(b) 9
(c) 34
(d) 435
(e) 219
Ans. (a)
Solution.
02 + 4 = 4
12 + 2 = 3
32 + 0 = 9
62 - 2 = 34
102 - 4 = 96
152 - 6 = 219
212 - 8 = 433 ≠ 435
(v) 157.5, 45, 15, 6, 3, 2, 1
(a) 1
(b) 2
(c) 6
(d) 157.5
(e) 45
Ans. (a)
Solution. 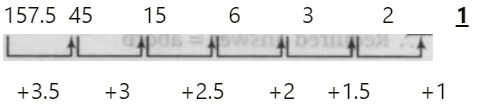
The number should be 2 in place of 1.
Different types of Number Series
There are some format of series which are given in Exams.
- Perfect Square Series: This Types of Series are based on square of a number which is in same order and one square number is missing in that given series.
Examples:
(i) 841, ?, 2401, 3481, 4761
Ans. 292, 392, 492, 592, 692
(ii) 1, 9, 25, ?, 81, 121
Ans. 12, 32, 52, 72, 92, 112
(iii) 289, 225, 169, ?, 81
Ans. 172, 152, 132, 112, 92 - Perfect Cube Series: This Types of Series are based on cube of a number which is in same order and one cube number is missing in that given series.
Examples:
(i) 3375, ?, 24389, 46656, 79507
Ans. 153, 223, 293, 363, 433
(Each cube digit added with seven to become next cube number)
(ii) 729, 6859, 24389, ?, 117649, 205379
Ans. 93, 193, 293, 393, 493, 593
(iii) 1000, 8000, 27000, 64000, ?
Ans. 103, 203, 303, 403, 503 - Ration Series: This type of series are based on ration series, where sequences are in form of ratio of difference between the numbers. All numbers are arranged in ratio sequence order.
- Geometric Series: This type of series are based on ascending or descending sequence of numbers and each continuous number is obtained by multiplying or dividing the preceding number with static number.
Examples:
(i) 3, ?, 45, 144, 585
Ans. 3 x 0 +9 = 9, 9 x 1 + 9 = 18, 18 x 2 + 9 = 45, 45 x 3 + 9 = 144, 144 x 4 + 9 = 585.
(ii) 5, 45, 405, 3645, ?
Ans. 5 x 9 = 45, 45 x 9 = 405, 405 x 9 = 3645, 3645 x 9 = 32805.
(iii) 73205, 6655, 605, 55, ?
Ans. 5 x 11 = 55, 55 x 11 = 605, 605 x 11 = 6655, 6655 x 11 = 73205. - Two stage Type Series: A two stage Arithmetic series is one in which the formation of arithmetic series are obtained from differences of continuous numbers themselves.
Examples:
(i) 3, 9, 18, 35, 58,......
(ii) 6, 9, 17, 23,...... - Mixed Series: This type of series has more then one different order are given, which has arranged in alternatively in a single series. This mixed series Examples are described separately.
|
177 videos|221 docs|199 tests
|
FAQs on Introduction & Examples: Number Series - General Intelligence and Reasoning for SSC CGL
| 1. What is Number Series? |  |
| 2. What are some shortcuts or tricks to solve Number Series? |  |
| 3. What kind of questions can be asked in Number Series in exams? |  |
| 4. What are some examples of Number Series patterns? |  |
| 5. How can I improve my Number Series skills for exams? |  |

















