Important Concepts: Number System | General Test Preparation for CUET UG - CUET Commerce PDF Download
Introduction
- A system is a set of principles or procedures according to which something is done.
- Number System is a set of principles according to which numbers are represented and various arithmetic operations like addition, subtraction, multiplication, etc, are applied to them. This lays down the basic rules on how various digits and symbols are used.
- Whenever we change the principles, we get a new number system. This results in various types of number systems.
- Some examples of number systems are:
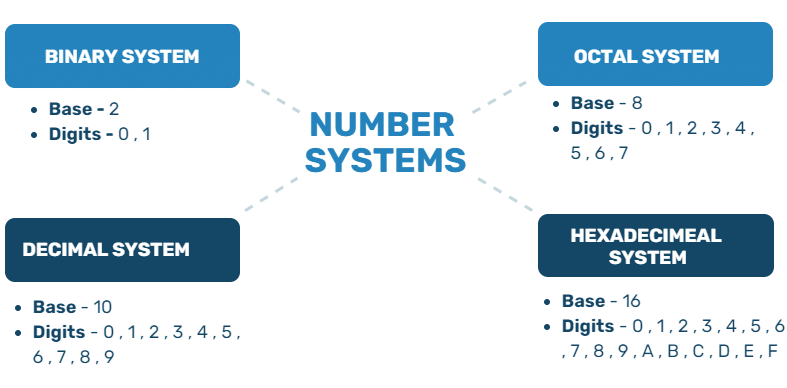 Types of Number Systems(i) Base is defined as the number of digits we use to represent the numbers.
Types of Number Systems(i) Base is defined as the number of digits we use to represent the numbers.
(ii) Digits are the tools that are used to represent numbers.
We will be talking about various number systems and their bases in subsequent chapters. The standard number system that we use across the world is the decimal number system. The Decimal Number System has a base "10" as it uses 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to represent all the numbers.
Face Value and Place Value
- Face Value: The Value of the digit itself is referred to as the face value of a particular Digit. In the decimal number system, we use the 10 digits, as mentioned above. Wherever used, the face value remains the same.
Example: The face value of 5 is 5 in 568 and 1285 and even 58738. - Place: The place value of a number depends on the place it is at. The various places and the corresponding multipliers of the places in a decimal number system are listed below. We will be starting from the leftmost side and moving to the right place by place.
Example: For a number 786543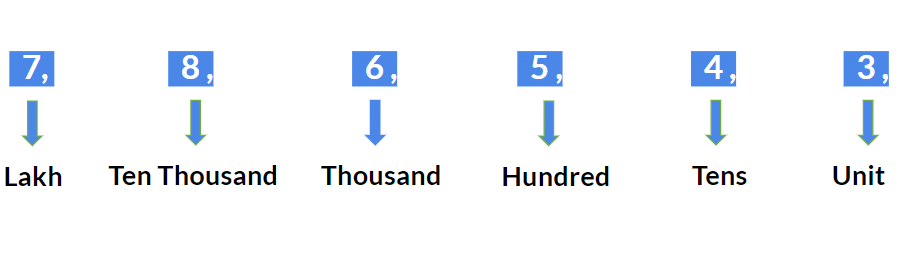

- Place Value of a digit in a particular number system is defined as the face value of the number multiplied by the corresponding place. In the decimal system, the value of the place will be as mentioned in the table above.
Example: The place value of 5 is 500 in 568, and 5 is 50000 in 58738.Question for Important Concepts: Number SystemTry yourself:What is the difference in the two Place Values and Two Face Values of digit 7 in the given number - 78687View Solution
In this chapter we are going to talk about the Numbers, their properties and their classifications. As discussed earlier all these properties will be limited to decimal number system only since that is the basis of all the question asked. The concepts discussed in this chapter will be your first step towards a general understanding of the mathematics requirements to clear any entrance exams. As we proceed you will realize that you have already learnt most of these concept in school.
Types of Numbers
1. Natural Number
The primary application of mathematics is counting. That is where the very first category of numbers comes in, i.e. natural numbers or commonly as known as counting Numbers.
Features of Natural Numbers
- These are the complete numbers, i.e. fractions/decimals, are not included.
- Zero is not included.
- Negatives are not included.
- They are represented by "N."
- N = {1, 2, 3, 4, 5.........infinity}
2. Whole Numbers
Natural numbers, along with 0, form a set of numbers known as Whole numbers. Since '0' is a representation of the absence of anything and is not used for counting, they are not called the counting numbers.
Features of Whole Numbers
- These are the complete numbers, i.e. fractions/decimals, are not included.
- Zero is included.
- Negatives are not included.
- They are represented by "W".
- W = {0, 1, 2, 3, 4, 5.........infinity}.

3. Integers
Numbers less than 'zero' are represented with a negative sign along with them and are referred to as negative numbers.
Whole numbers, along with negative of natural numbers form a set of numbers known as integers.
Features of Integers
- These are the complete numbers, i.e. fractions/decimals, are not included.
- Zero is included.
- Negatives are included.
- They are represented by "I".
- I = {- infinity.......-3, -2, -1, 0, 1, 2, 3 ......... infinity}.
4. Fractions
The word ‘fraction’ has been derived from the Latin ‘fractus’ which means “broken”. Fraction represent part of a whole. When we divide a whole into pieces, each part is a fraction of the whole.
Example: 1/2, 3/5, 2/7, 10/21
A fraction has two parts. The number on the top of the line is called the numerator. The number below the line is called the denominator.
Types of Fractions
Fractions are generally of two types on the basis of representation:
(i) Simple Fraction
Example: 30/7
(ii) Mixed Fraction
Example: 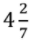
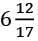 into a simple fraction.
into a simple fraction.
5. Decimal Numbers
These are nothing but a form of representation of fractions. We make the value of the denominator as unity, i.e. "1". They can be both negative and positive.
Example: 2.5, 1.25, 1.3333 ......., 2.666....., 2.8284.....
Types of Decimal Numbers
Decimal numbers are majorly divided into two categories:
- Terminating Decimal Numbers: The decimal numbers with a definite end. Example: 2.5, 1.25
- Non-Terminating Decimal Numbers: The decimal numbers without a definite end. Example: 1.3333 ......., 2.666....., 2.8284.....
Non-Terminal Decimal Numbers are further divided into two categories:
(i) Recurring non-terminating decimal numbers: The non-terminating decimal numbers with digits after the decimal repeating again and again.
(ii) Non-recurring non-terminating decimal numbers: The non-terminating decimal numbers with digits after the decimal do not repeat but have a completely random pattern. These are the irrational numbers, which we will discuss ahead in the same chapter.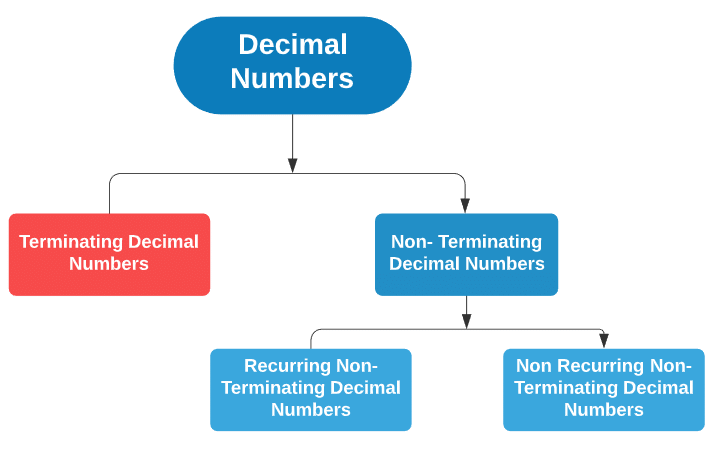 Classification of Decimal Numbers
Classification of Decimal Numbers
6. Rational Numbers
All those numbers that can be represented in the form of p/q where p and q are integers with q ≠ 0 are known as Rational numbers. All the integers, fractions, terminating decimal numbers and non-terminating recurring decimal numbers fall under the category of Rational Numbers.
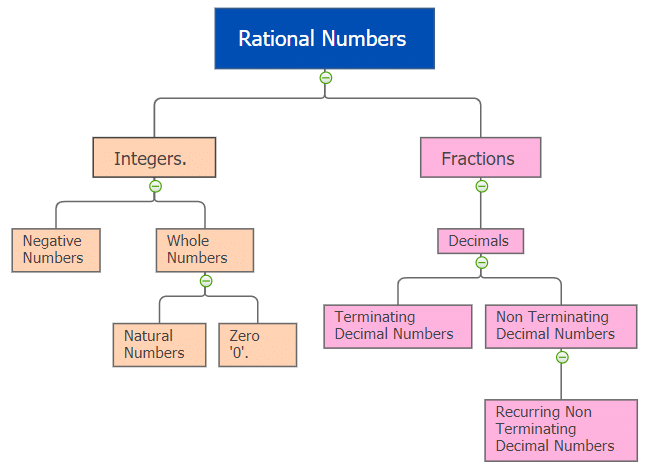
7. Irrational Numbers
All those numbers that are not rational are known as irrational numbers. Non-reciprocating, non-terminating decimal numbers are irrational numbers. The Square Roots, Cube Roots, etc., of natural numbers turn out to be irrational numbers.
Example: √3 = 1.7320.... , √8 = 2.8284 ......, 3√4 = 1.5874 .......
Converting a Terminating Decimal Number in p/q form:
Example: Convert 80.125 in p/q form
- Count how many digits are thereafter decimal, 3 in this case.
- Remove the decimal and divide the number so received by as many 10's as the counting in step 1.
⇒ 80.125 = 80125/1000 = 641/8
Converting a non-terminating recurring decimal number in p/q form:
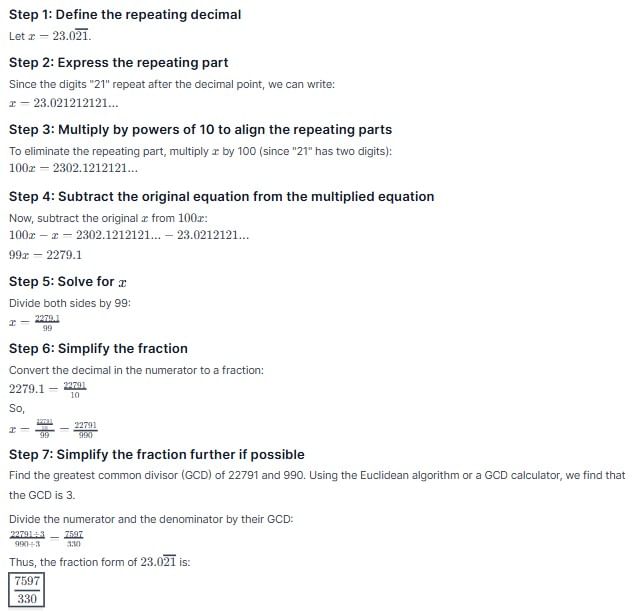
Example: Convert 80.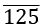 in p/q form.
in p/q form.
- Let the number be equal to x
⇒ x = 80.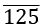
- Count how many digits are thereafter decimal, 3 in this case.
- Multiply by as many tens on both sides, i.e. 1000, in this case.
⇒ 1000x = 80125.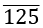
- Subtract
from
⇒ 999x = 80045
⇒ x = 80045 / 999
Example: Convert 80. 1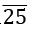 in p/q form.
in p/q form.
- Let 80.1
= x
- Multiply both sides by 100
⇒- Subtract
from
⇒ 99x = 7922.4
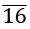 in p/q form
in p/q form
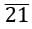 in p/q form
in p/q form
The process we have applied in the examples above is too time-consuming. We need a method that can do the same process in much less time. For that, we have a formula with which you can have the answer in a single step.
Every terminating recurring decimal number has 3 parts:
(Taking the example of: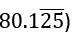
(i) Digits before the decimal (80).
(ii) No. of digits with the bar on them after the decimal (2).
(iii) No. of digits without a bar on them after the decimal (1).
Rational form: All the digits without decimal written once - All the digits without bar written once / as many 9's as no. of digits with bar on them after decimal followed by as many 0's no. of digits without bar on them after decimal.
Example: Convert 80.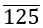 in p/q form
in p/q form
- All the digits are written once = 80125
- All the digits without bar written once = 80
- No. of digits with bar after decimal = 3
- No. of digits without bar after decimal = 0
- Rational form = (80125 - 80) / 999 = 80045 / 999
Example: Convert 80.1 in p/q from
in p/q from
- All the digits are written once = 80125
- All the digits without Bar written once = 801
- No. of digits with bar after decimal = 2
- No. of digits without bar after decimal = 1
- Rational form = (80125 - 801) / 990 = 79324 / 990
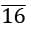 in p/q from
in p/q from
8. Real Numbers
- Rational numbers, as well as irrational numbers together, form the real numbers. As per the definition, all the numbers that can be represented on a number line are known as real numbers.
- All the categories that we have discussed till now fall in the set of Real numbers, including the irrational numbers. They can also be represented on a number line.
9. Imaginary Numbers
- All those numbers that actually do not exist in a number system but assume their presence for the sake of calculations are known as imaginary numbers.
- They cannot be represented on number lines. They are also called complex numbers.
Example: √−3, √−16, 4√−8
Note: The study of complex numbers is not important from Aptitude Testing point of view. So, we will not take this topic any further.
10. Odd and Even Numbers
- Even Numbers are those that are divisible by 2. They are the numbers with their unit digit as either 2, 4, 6, 8 or 0. The general expression of even numbers is 2n, where n is a whole number.
- Odd Numbers are those that are not divisible by 2. They are the numbers with their unit digit as either 1, 3, 5, 7 or 9. The general expression of odd numbers is 2n+1 , where n is a whole number.
11. Prime and Composite Numbers
(a) Prime Numbers: Being Prime is a property of Natural Numbers. All those numbers which are divisible by exactly 2 numbers, i.e. itself and unity "1".
Example: 2, 3, 5, 7, 11 etc.
(b) Composites are the numbers which are divisible by more than 2 numbers, i.e. itself, unity "1" and at least one other.
Example: 4, 6, 8, 9, 10, etc.
1 is neither Prime nor Composite.

➢ Property of Prime Numbers
- All Prime numbers greater than 3 are of the form 6n ± 1, but not all numbers of the form 6n ± 1 are Prime. This property means that when prime numbers greater than 3 are divided by 6 they leave a remainder of 1 or 5.
12. Co - Prime Numbers
- This is a property of a pair or more than two natural numbers.
- Two numbers are said to be co-prime if the only number that can completely divide both the numbers is 1. No number other than 1 can divide both the given numbers of the pair.
- These numbers in themselves can be prime or composite. 1 is co-prime with all the natural numbers other than 1.
Example: (3, 7); (4, 15); (3, 10) etc. - A set of numbers is said to be co-prime if their HCF is 1. We will be learning about HCF in the following chapters.
Example: (3, 7, 11); (4, 15, 10); (3, 10, 8) etc.
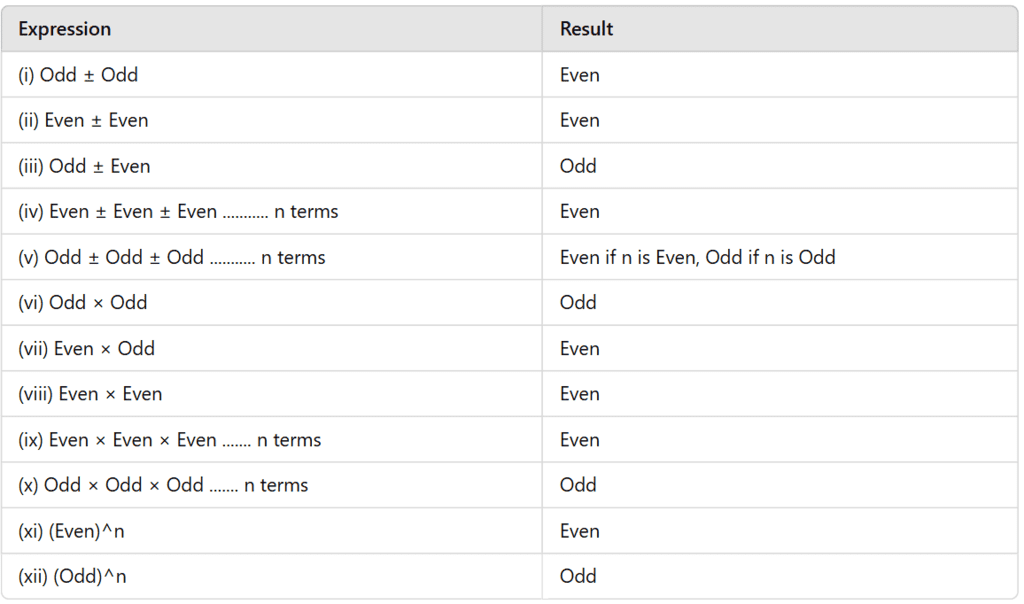
Operations on Whole Numbers:
|
164 videos|626 docs|1127 tests
|
FAQs on Important Concepts: Number System - General Test Preparation for CUET UG - CUET Commerce
| 1. What is the difference between face value and place value in the number system? |  |
| 2. How do you determine the face value of a digit in a number? |  |
| 3. How do you find the place value of a digit in a number? |  |
| 4. What are the different types of numbers in the number system? |  |
| 5. Why is understanding the number system important in mathematics? |  |

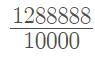 =
= 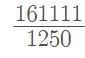 [Just dividing the numerator and denominator by same factor ]
[Just dividing the numerator and denominator by same factor ]
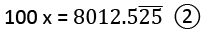
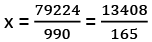
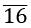 = x
= x 
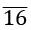
 from
from