Relations & Its Types | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Relations |

|
| Representation of a Relation |

|
| Domain and Range of a Relation |

|
| Total Number of Relations |

|
| Types of Relations |

|
| Solved Examples |

|
| Equivalence class |

|
| Short Answer Type Questions |

|
Relations
Given any two non-empty sets A and B, a relation R from A to B is a subset of the Cartesian product A × B and is derived by describing a relationship between the first element (say x) and the other element (say y) of the ordered pairs in A & B.
Further, if (x, y) ∈ R, then we say that x is related to y and write this relation as x R y. Hence, R = {(x, y); x ∈ A, y ∈ B, x R y}.
Note: Ordered pairs means (x, y) and (y, x) are two different pairs.
Example: If R is a relation between two sets A = {1,2,3} and B = {1,4,9} defined as "square root of ". Here, 1R1, 2R4, 3R9
Then, R = {(1, 1), (2, 4), (3, 9)}.
| x | y |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Representation of a Relation
1. Roster form: In this form, a relation is represented by the set of all ordered pairs belonging to R. If R is a relation from set A = {1,2,3,4} to set B = {1,4,9,16,25} such that the second elements are square of the first elements. So, R can be written in roster form as
R = {(1,1),(2,4),(3,9),(4,16)}
2. Set-builder form: In this form the relation R from set A to B is as
R = {(x,y): x∈A, y∈B; The rule which asociates x and y}
Example: R = {(1,1),(2,4),(3,9),(4,16)} can be written in set-builder form as
R = {(x,y): x∈A, y∈B; y=x2}, where A = {1,2,3,4}, B = {1,4,9,16}.
3. Visual Representation (Arrow Diagram)
In this form of representation, we draw arrows from first element to the second element for all ordered pairs belonging to R.
Example: Let R = {(1,5),(1,6),(2,5),(3,5)} from set A = {1,2,3} to set B = {5,6}
It can be represented by the following arrow diagram.
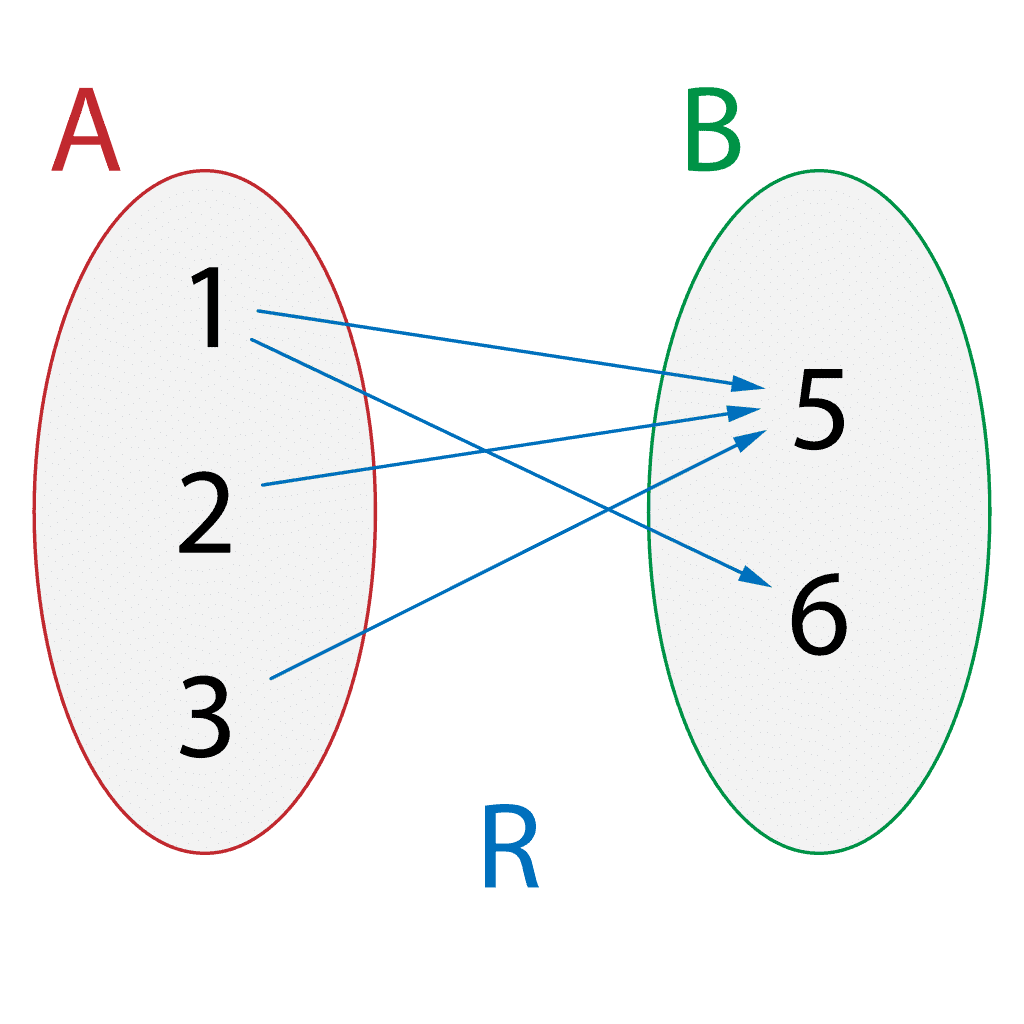
Domain and Range of a Relation
1. Domain of a Relation
Let R be a relation from A to B. The domain of relation R is the set of all those elements a ∈ A such that (a,b) ∈ R for some b ∈ B.
Thus domain of R = {a ∈ A: (a,b) ∈ R for some b ∈ B}
= set of first elements of all the ordered pairs belonging to R
2. Range of a Relation
Let R be a relation from A to B. The range of R is the set of all those elements b ∈ B such that (a,b) ∈ R for some a ∈ A.
Thus range of R = {b ∈ B: (a,b) ∈ R for some a ∈ A}
= set of second elements of all the ordered pairs belonging to R.
3. Co-domain of a Relation
If R be a relation from A to B, then B is called the co-domain of relation R.
Clearly range of a relation ⊆ co-domain.
Total Number of Relations
For two non-empty finite sets A and B. If the number of elements in A is h i.e., n(A) = h & that of B is k i.e. n(B) = k, then the number of ordered pair in the Cartesian product will be n(A × B) = hk. The total number of relations is 2hk.
Types of Relations
1. Empty Relation
If no element of set X is related or mapped to any element of X, then the relation R in A is an empty relation, i.e, R = Φ. Think of an example of set A consisting of only 100 hens in a poultry farm. Is there any possibility of finding a relation R of getting any elephant in the farm? No! R is a void or empty relation since there are only 100 hens and no elephant.
2. Universal Relation
A relation R in a set, say A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. Also called Full relation. Suppose A is a set of all - natural numbers and B is a set of all whole numbers. The relation between A and B is universal as every element of A is in set B. Empty relation and Universal relation are sometimes called trivial relation.
3. Identity Relation
In Identity relation, every element of set A is related to itself only. I = {(a, a), ∈ A}.
Example: If we throw two dice, we get 36 possible outcomes, (1, 1), (1, 2), … , (6, 6). If we define a relation as R: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}, it is an identity relation.
4. Inverse Relation
Let R be a relation from set A to set B i.e., R ⊆ A × B. The relation R-1 is said to be an Inverse relation if R-1 from set B to A is denoted by R-1 = {(b, a): (a, b) ∈ R}. Considering the case of throwing of two dice if R = {(1, 2), (2, 3)}, R-1 = {(2, 1), (3, 2)}. Here, the domain of R is the range of R-1 and vice-versa.
5. Reflexive Relation
If every element of set A maps to itself, the relation is Reflexive Relation. For every a ∈ A, (a, a) ∈ R.
Example: Let A = {1, 2, 3}
Then R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2)}
R3 = {(1, 1), (2, 2), (1, 2)}
Clearly ,R1, R2 both are reflexive relation, but R3 is not reflexive relation because (3, 3) ∉ R3
Note: Every identity relation is reflexive relation,but every reflexive relation is not identity relation.
6. Symmetric Relation
A relation R on a set A is said to be symmetric if (a, b) ∈ R then (b, a) ∈ R, a & b ∈ A.
Example: Let A = {1, 2, 3}
Then R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
R3 = {(1, 1), (2, 2), (1, 2)}
Clearly, R1, R2 both are symmetric relation, but R3 is not symmetric relation because (1, 2) ∈ R3 , but (2, 1) ∉ R3
Note: A relation is called symmetric if R = R-1.
7. Transitive Relation
A relation in a set A is transitive if, (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R, a, b, c ∈ A
Example: Let A = {1, 2, 3}
Then R1 = {(1, 1), (2, 2), (3, 3)}
R2 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
R3 = {(1, 1), (2, 2), (1, 2), (2, 3)}
Clearly ,R1, R2 both are transitive relation, but R3 is not transitive relation because(1, 2) & (2, 3) ∈ R3, but (1, 3) ∉ R3
Note:
Every empty relation defined on a non empty set is always symmetric and transitive but not reflexive.
Every universal set defined on non empty set is always reflexive, symmetric and transitive.
8. Equivalence Relation
A relation is said to be equivalence if and only if it is Reflexive, Symmetric, and Transitive.
Example: If we throw two dices A & B and note down all the possible outcome.
Define a relation R= {(a, b): a ∈ A, b ∈ B}, we find that {(1, 1), (2, 2), …, (6, 6) ∈ R} (reflexive). If {(a, b) = (1, 2) ∈ R} then, {(b, a) = (2, 1) ∈ R} (symmetry). If {(a, b) = (1, 2) ∈ R} and {(b, c) = (2, 3) ∈ R} then {(a, c) = (1, 3) ∈ R} (transitive)
Solved Examples
Q.1. If A is a set of all triangles and the relation R is defined by “is congruent to” prove that R is an equivalence relation.
Ans.
(i) R is reflexives as every triangle is congruent to itself.
(ii) R is symmetric: if a triangle x is congruent to another triangle y, then the triangle y is congruent to the triangle x.
(iii) If ‘a triangle x is congruent to a triangle y and y is congruent to a third triangle z, then x is also congruent to z.
Hence the relation R is transitive. (i), (ii) and (iii) ⇒ that the relation R is an equivalence relation.
Q.2. Three friends A, B, and C live near each other at a distance of 5 km from one another. We define a relation R between the distances of their houses. Is R an equivalence relation?
Ans.
- For an equivalence Relation, R must be reflexive, symmetric and transitive.
- R is not reflexive as A cannot be 5 km away to itself.
- The relation, R is symmetric as the distance between A & B is 5 km which is the same as the distance between B & A.
- R is transitive as the distance between A & B is 5 km, the distance between B & C is 5 km and the distance between A & C is also 5 km. Therefore, this relation is not equivalent.
Equivalence class
An equivalence class is subset of a given set in which each element is related with each other. Moreover equivalence class can be found if the given relation on given set is an equivalence relation.
Example: Let A = {1, 3, 5, 9, 11, 18} and a relation on A given by
R = {(a, b) | a - b is divisible by 4 } find all equivalence classes.
Solution. Clearly R ={(1, 1), (3, 3), (5, 5), (9, 9), (11, 11), (18, 18), (1, 5)(5, 1), (1, 9), (3, 11)(11, 3), (5, 9), (9, 5)}
Now A1 = {1, 5, 9}, A2 = {3, 11}, A3= {18}
Hence A1, A2, A3 are called equivalence classes of a set A on the given relation R
Moreover we can represent these classes in a very specific way as below:
A1 = [1] or [5] or [9]
A2 = [3] or [11]
A3 = [18]
Clearly, A1, A2 , A3 are disjoint and A1∪ A2 ∪ A3 = A and A1 ∩ A2 ∩ A3= ∅
Note:
- All elements of Ai are related to each other, for all i.
- No element of Ai is related to any element of Aj, i≠ j.
- ∪ Aj = X and Ai ∩Aj = ∅, i ≠ j.
The subsets Ai are called equivalence classes and are called partitions or subdivisions of set A and these are mutually disjoint to one another.
Short Answer Type Questions
Q.1. Show that the number of equivalence relation in the set {1, 2, 3} containing (1, 2) and (2, 1) is two.
Ans. A = {1, 2, 3}
The maximum possible relation (i.e. universal relation) is
R = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)}
The smallest equivalence relation R1 containing (1 , 2) and (2 , 1) is
R1 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
we are left with four pairs (from universal relation) i.e. (2, 3), (3, 2), (1, 3) and (3, 1)
If we add (2, 3) to R1, then for symmetric by we must add (3, 2) and now for transitivity we are forced to add (1, 3) and (3, 1)
Thus the only relation bigger than R1 is universal relation i.e R
∴ The no. of equivalence relations containing (1, 2) and (2, 1) is two.
Q.2. If 𝑅 = {(𝑥, 𝑦) ∶ 𝑥2 + 𝑦2 ≤ 4 ; 𝑥, 𝑦 ∈ 𝑧} is a relation on 𝑧. Write the domain of R.
Ans. R = {(0, 1), (0, -1), (0, 2), (0, -2), (1, 1), (1, -1), (-1, 0), (-1, 1), (-1, -1), (2, 0), (-2, 0)}
∴ Domain of R = {0, 1 , -1, 2, -2}
(i.e the first domain of each ordered pairs)
Q.3. Let R = {(𝑥, 𝑦) : ∣𝑥2 − 𝑦2∣ < 1} be a relation on set A = {1, 2, 3, 4, 5}. Write R as a set of ordered pairs.
Ans. A = {1, 2, 3, 4, 5}
for ∣𝑥2 − 𝑦2∣ < 1 : 𝑥 should be equal to 𝑦
∴ R = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}
Q.4. R is a relation in Z defined as (𝑎, 𝑏) ∈ 𝑅 ⇔ 𝑎2 + 𝑏2 = 25. Find the range.
Ans. We have, 𝑎2 + 𝑏2 = 25 and 𝑎 , 𝑏 ∈ 𝑧
∴ R = {(0, 5), (0, -5), (3, 4), (3, -4), (-3, 4), (-3, -4), (4, 3), (4, -3), (-4, 3), (-4, -3), (5, 0), (-5, 0)}
∴ Range = {-5, 5, 4, -4, 4, 3, -3, 0}
(i.e. second elements of each order pairs)
|
172 videos|503 docs|154 tests
|
FAQs on Relations & Its Types - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a relation and how is it represented? |  |
| 2. What is the domain and range of a relation? |  |
| 3. How many total relations can be formed between two sets with m and n elements? |  |
| 4. What are the different types of relations? |  |
| 5. What is an equivalence class in a relation? |  |

















