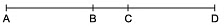Introduction to Euclid's Geometry Class 9 Worksheet Maths
Q1. If A, B and C are three points on a line, and ‘B’ lies between ‘A’ and ‘C’ (as shown in the figure), then prove that: AB + BC = AC
Sol.
In the figure given above, AC coincides with AB+ BC
From Euclid's Axiom 4: Things which coincide with one another are equal to each other.
So, we write AB+BC=AC
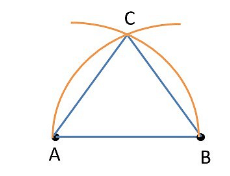
Q2. Prove that an equilateral triangle can be constructed on any given line segment.
Sol. Equilateral triangle is a angle with all sides are equal
1. Draw a line segment AB of the any length.
2. Take compass put the pointy end at point A & pencile at point B.
3.Draw an arc.
Here we draw an arc of radii AB
4. Now put the pointy end at B and pencil at A.
5. Draw another arc.
Here we draw an arc of radii BA .
6. Mark the intersecting point as C.
7. Join point A to point C by a straight line .
8. Join point B to point C by a straight line
ABC is the triangle.
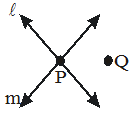
Q3. Prove that two distinct lines cannot have more than one point in common.
Ans 3.
Given: Two distinct line l and m
To Prove: Lines l and m have at most one point in common.
Proof: Two distinct lines l and m intersect at a point P.
Let us suppose they will interact at another point, say Q (different from P).
It means two lines l and m passing through two distinct point P and Q.
But it is contrary to the axiom 5.1 which states that “Given two distinct points, there exists one and only one line pass through them”
So our supposition is wrong
Hence, two distinct lines cannot have more than one point in common
Q4. Is the following statement true? “Attempts to prove Euclid’s fifth postulate using the other postulate and axioms led to the discovery of several other geometries.”
True
Q5. Fill in the blanks to complete the following axioms :
(i) Things, which are equal to the same things, are ...............................
(ii) If equals are added to equals, the ...............................
(iii) If equals are subtracted from equals, ...............................
(iv) Things which coicide with one another are ...............................
(v) The whole is greater than the ...............................
(vi) Things which are double of the same things are ...............................
(vii) Things which are halves of the same things, are ...............................
Sol (i) equal to one another
(ii) wholes are equal
(iii) the remainders are equal
(iv) equal to one another
(v) part
(vi) equal to one another
(vii) equal to one another
Q6. In the figure, line PQ falls on AB and CD such that (∠1 + ∠2) < 180°. So, lines AB and CD, if produced will intersect on the left of PQ. This is an example of which Postulate of Euclid?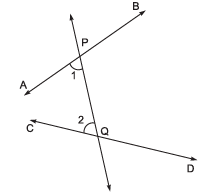
Sol. Fifth postulate
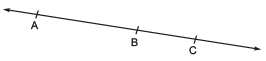
Q7. In the given figure, if AC = BD, then prove that AB = CD
Hint: AC = BC [given] ...(1)
∴ AC = AB + CD [∵ B lies between A and C] ...(2)
BD = BC + CD [∵ C lies between B and D] ...(3)
From (1), (2) and (3) we have: AB + BC = BC + CD or AB = CD
Sol
From the figure, it can be observed that
AC = AB + BC
BD = BC + CD
It is given that AC = BD
AB + BC = BC + CD (1)
According to Euclid’s axiom, when equals are subtracted from equals, the remainders are also equal.
Subtracting BC from equation (1), we obtain
AB + BC − BC = BC + CD − BC
AB = CD
Q8. Write ‘true’ or ‘false’ for the following statement:
(i) Three lines are concurrent if they have a common point.
(ii) A line separates a plane into three parts, namely the two half-planes and the line itself. (iii) Two distinct lines in a plane cannot have more than one point in common.
(iv) A ray has two endpoints.
(v) A line has indefinite length.
Sol. (i), (ii), (iii) and (v) are true.
Q9. How many lines can pass through:
(i) one point
(ii) two distinct points?
Sol (i) infinite
(ii) one only
Q10. AB and CD are two distinct lines. In how many points can they at the most intersect?
Sol. one point only
Q11. Prove that any line segment has one and one mid-point.
Sol. Let AB be a line segment
and let D and E be its two midpointsnow, since D is the midpoints of ABso, AD=DBAB=AD+DB=2AD-(1)Also E is a point of ABSo, AE=EBAB=AE+EB=2AE-(2)From eq 1 &22AD=2AED and E coincide to each otherAB has one and only one mid pointsHence every line segments has one and only one midpoint.
Q12. In the given figure, AB = BC, P is midpoint of AB and Q is midpoint of BC. Show that AP = QC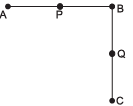 Hint: Things which are halves of the same thing (or equal things) are equal to one another.
Hint: Things which are halves of the same thing (or equal things) are equal to one another.
Sol.
We have AB = BC...(1) [Given]
Now, A, M. B are the three points on a line, and M lies between A and B, then
AM + MB = AB ...(2)
Similarly, BN * NC = BC....(3)
So. we get AM + MB = BN * NC
From (1), (2). (3) and Euclid's axiom 1
Since M Is the mid-point of AB and N is the mid-point of BC. therefore
2AM = 2NC
Using axiom 6, things which are double of the same thing are equal to one another.
Hence, AM = NC.
|
40 videos|471 docs|57 tests
|
FAQs on Introduction to Euclid's Geometry Class 9 Worksheet Maths
| 1. What is Euclid's Geometry? |  |
| 2. What are the fundamental principles of Euclid's Geometry? |  |
| 3. How did Euclid's Geometry influence modern mathematics? |  |
| 4. What are some famous theorems derived from Euclid's Geometry? |  |
| 5. How can one apply Euclid's Geometry in real-world scenarios? |  |