Introduction: Fractions & Decimals | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
| Table of contents |

|
| What are Fractions? |

|
| Types of Fractions |

|
| Multiplication of Fractions |

|
| Division of Fractions |

|
| Some Solved Questions |

|
What are Fractions?
The term fraction comes from the Latin word "Fractus," which means broken. It signifies a portion of an entire, made up of several equal parts from the whole.
For instance, pizza slice.
 Fractions of a Pizza Slice
Fractions of a Pizza Slice
Representation of Fractions
A fraction is represented by 2 numbers on top of each other, separated by a line. The top number is called the numerator, and the bottom number is the denominator. For example, 3/4, which means 3 parts out of 4 equal parts.
What is Fraction on a Number Line?
A fraction number line, as the name suggests, represents fractions on a number line.
- In order to represent a fraction on a number line, we divide the line segment between two whole numbers into n equal parts, where n is the denominator.
- It is a horizontal number line that displays two whole numbers at either end of the line.
- We can identify and plot all the fractions lying between these two whole numbers.
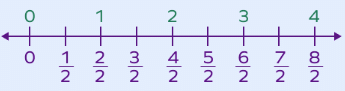 Fractions on number line
Fractions on number line
Types of Fractions
(i) Proper Fraction: It is a fraction whose denominator is greater than the numerator, such as
Example: 1/4, 7/9, 50/51. Proper fractions are greater than 0 and less than 1.
Suppose we have to mark 5⁄6 on the number line.
It shows as:
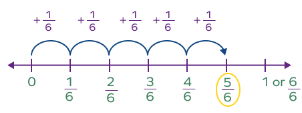 Proper Fraction
Proper Fraction
(ii) Improper Fractions: These Fractions have a numerator that is greater than or equal to the denominator. Examples: 7/5,19/6,101/45, etc. Improper fractions are greater than 1 or equal to 1.
To represent an improper fraction on a number line, we can always convert it to a mixed fraction Suppose, we have to plot 5/2 on the number line.
- Step 1: First, look at the denominator. The denominator is 2. So, split each whole into 2 equal parts starting from 0.
- Step 2: Then, look at the numerator. The numerator is 5. So, start at 0 and count forward 5 parts. The result is 5/2.
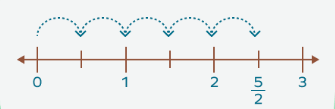 Improper Fraction
Improper Fraction
(iii) Mixed fractions: In this fractions, are a combination of a whole number and a proper fraction. Example: 43/5.
The mixed numbers or the mixed fractions are always greater than 1 since their numerator is greater than the denominator.
Let’s understand how to represent a mixed fraction on a number line. Suppose, we have to mark 334 on the number line.
- Step 1: First, find the whole number part of the mixed number. In this example, the whole number part is 3. So, the mixed fraction lies between 3 and 4.
- Step 2: The fractional part is 34. Thus, divide the above line segment into four equal parts. Each part represents 14.
- Step 3: Go to the fractional part. In this example, go to 34.
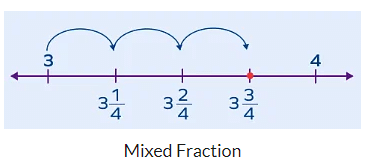
(iv) Like Fraction: In this type, there are fractions with the same denominator.
Example: 1/4, 2/4, 3/4.
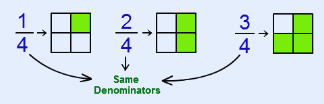 Like Fraction(v) Unlike Fraction: In this fraction, there are fractions with different denominators.
Like Fraction(v) Unlike Fraction: In this fraction, there are fractions with different denominators. 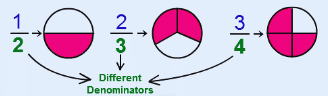 Unlike Fraction
Unlike Fraction
(vi) Equivalent Fraction: Equivalent fractions are fractions that have different numerators and denominators, but they still represent the same value.
For example: Let us mark 1/2 and 2/4.
- To represent 1/2, we divide 0 and 1 into 2 parts and choose the second marking.
- To represent 2/4, we divide 0 and 1 into 4 parts and choose the second marking.
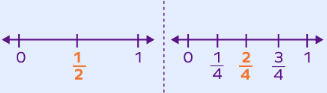 Equivalent Fraction
Equivalent Fraction
Multiplication of Fractions
- Fractions are represented in the “p/q” format and this form is most preferred for carrying out multiplication of 2 or more fractions.
- Multiplication of fractions is a simple operation.
- Multiply the numerator of all the fractions separately and multiply the denominators of all the fractions separately to obtain the final numerator and denominator.
- For example,
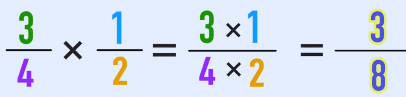 Multiplication of Fractions
Multiplication of Fractions
Multiplication of a Fraction with a Whole number
- Multiplying fractions with whole numbers is an easy concept.
- We just need to convert the whole number into a fraction by writing 1 as the denominator and writing the whole number as the numerator.
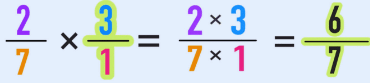 Multiplication of a fraction with a whole number
Multiplication of a fraction with a whole number
Example: To multiply a fraction by a whole number, multiply the numerator of the fraction by the whole number, and keep the denominator the same.
2/3 * 4 = 8/3
Therefore, when you multiply the fraction 2/3 by the whole number 4, the result is 8/3.
Multiplication of Mixed Fractions
- A mixed fraction is one that has a whole number and a fraction together. For example,
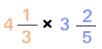
- To multiply them we convert each mixed fraction into a simple fraction and then multiply these fractions.
 Multiplication of mixed fraction
Multiplication of mixed fraction
(i) Fraction as an Operator ‘Of’
The ‘of’ operator basically implies multiplication.
Example: 1/5 of 2 = (1/5)×2= 2/5
or, 1/2 of 11 = (1/2) × 11 = 11/2
(ii) Multiplication of Fraction by a Fraction
To multiply two fractions, just multiply the numerators to get the numerator of the product, and multiply the denominators to get the denominator of the product.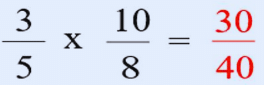 Multiplication of Fraction by a Fraction
Multiplication of Fraction by a Fraction
Example: To multiply fractions, multiply the numerators together and the denominators together.
1/2 * 3/4 = 3/8
Therefore, when you multiply the fraction 1/2 by the fraction 3/4, the result is 3/8.
(iii) Value of the Products
We know that the product of two whole numbers is bigger than each of the two whole numbers.
For example, 2× 4 = 8 and 8 > 4, 8 > 3.
when two proper fractions are multiplied, the product is less than each of the fractions. Or, we say the value of the product of two proper fractions is smaller than each of the two fractions.
The product of two improper fractions is greater than each of the two fractions.
Division of Fractions
- Dividing fractions is almost the same as multiplying them.
- Multiplying the fractions by reversing one of the two fraction numbers or by writing the reciprocal of one of the fractions.
- By reciprocal we mean, that if a fraction is given as a/b, then the reciprocal of it will b/a.
- Thus, interchanging the position of the numerator and denominator with each other.
- a/b ÷ c/d = a/b × d/c
Here are two examples of dividing fractions using the reciprocal method for a Class 7 Student:
Example 1:
Let's divide the fraction 2/3 by the fraction 3/4.
- Step 1: Write down the fractions.
Fraction 1: 2/3
Fraction 2: 3/4 - Step 2: Find the reciprocal of the second fraction.
Reciprocal of 3/4 is 4/3. - Step 3: Multiply the first fraction by the reciprocal of the second fraction.
2/3 ÷ 3/4 = 2/3 × 4/3 - Step 4: Multiply the numerators and denominators together.
2/3 × 4/3 = (2 × 4) / (3 × 3) = 8/9
Therefore, when you divide the fraction 2/3 by the fraction 3/4, the result is 8/9.
Example 2:
Let's divide the fraction 5/6 by the fraction 2/5.
- Step 1: Write down the fractions.
Fraction 1: 5/6
Fraction 2: 2/5 - Step 2: Find the reciprocal of the second fraction.
Reciprocal of 2/5 is 5/2. - Step 3: Multiply the first fraction by the reciprocal of the second fraction.
5/6 ÷ 2/5 = 5/6 × 5/2 - Step 4: Multiply the numerators and denominators together.
5/6 × 5/2 = (5 × 5) / (6 × 2) = 25/12
Therefore, when you divide the fraction 5/6 by the fraction 2/5, the result is 25/12.
Some Solved Questions
Q.1. Multiply 21/5 and 15/4
Multiplying 21/5 × 15/4 =
we get 51/4
Q.2. Shyama bought around 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala then bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
From the above question, it is given that,
Fruits bought by Shyama is = 5 kg 300 g
= 5 kg + (300/1000) kg
= 5 kg + 0.3 kg
= 5.3 kg
Fruits bought by Sarala is = 4 kg 800 g + 4 kg 150 g
= (4 + (800/1000)) + (4 + (150/1000))
= (4 + 0.8) kg + (4 + .150) kg
= 4.8 kg + 4.150kg
= 8.950 kg
So, Sarala bought more fruits.
|
77 videos|386 docs|39 tests
|
FAQs on Introduction: Fractions & Decimals - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What are fractions? |  |
| 2. What are the types of fractions? |  |
| 3. How do you multiply fractions? |  |
| 4. How do you divide fractions? |  |
| 5. Can you provide some solved questions related to fractions and decimals? |  |
















