Introduction to Mathematical Modelling | Control Systems - Electrical Engineering (EE) PDF Download
Modeling of Translational Mechanical Systems
Translational mechanical systems move along a straight line. These systems mainly consist of three basic elements. Those are mass, spring and dashpot or damper.
If a force is applied to a translational mechanical system, then it is opposed by opposing forces due to mass, elasticity and friction of the system. Since the applied force and the opposing forces are in opposite directions, the algebraic sum of the forces acting on the system is zero. Let us now see the force opposed by these three elements individually.
Mass
Mass is the property of a body, which stores kinetic energy. If a force is applied on a body having mass M, then it is opposed by an opposing force due to mass. This opposing force is proportional to the acceleration of the body. Assume elasticity and friction are negligible.
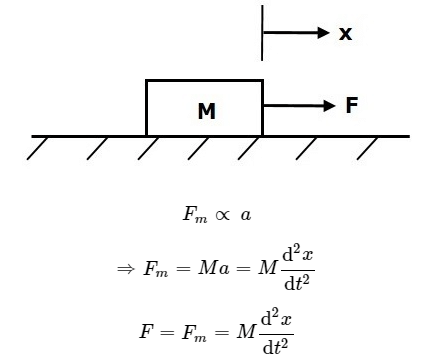
Where,
- F is the applied force
- Fm is the opposing force due to mass
- M is mass
- a is acceleration
- x is displacement
Spring
Spring is an element, which stores potential energy. If a force is applied on spring K, then it is opposed by an opposing force due to elasticity of spring. This opposing force is proportional to the displacement of the spring. Assume mass and friction are negligible.
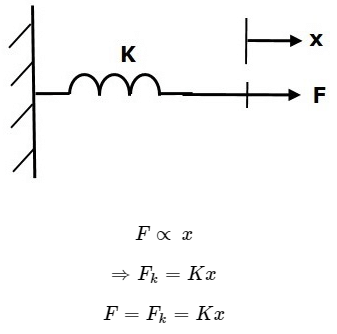
Where,
- F is the applied force
- Fk is the opposing force due to elasticity of spring
- K is spring constant
- x is displacement
Dashpot
If a force is applied on dashpot B, then it is opposed by an opposing force due to friction of the dashpot. This opposing force is proportional to the velocity of the body. Assume mass and elasticity are negligible.
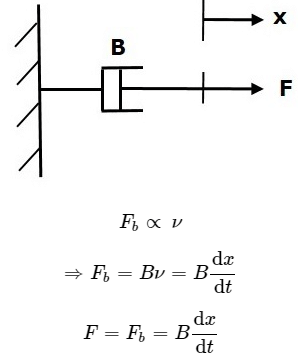
Where,
- Fb is the opposing force due to friction of dashpot
- B is the frictional coefficient
- v is velocity
- x is displacement
Modeling of Rotational Mechanical Systems
Rotational mechanical systems move about a fixed axis. These systems mainly consist of three basic elements. Those are moment of inertia, torsional spring and dashpot.
If a torque is applied to a rotational mechanical system, then it is opposed by opposing torques due to moment of inertia, elasticity and friction of the system. Since the applied torque and the opposing torques are in opposite directions, the algebraic sum of torques acting on the system is zero. Let us now see the torque opposed by these three elements individually.
Moment of Inertia
In translational mechanical system, mass stores kinetic energy. Similarly, in rotational mechanical system, moment of inertia stores kinetic energy.
If a torque is applied on a body having moment of inertia J, then it is opposed by an opposing torque due to the moment of inertia. This opposing torque is proportional to angular acceleration of the body. Assume elasticity and friction are negligible.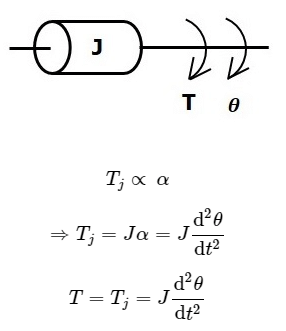
Where,
- T is the applied torque
- Tj is the opposing torque due to moment of inertia
- J is moment of inertia
- α is angular acceleration
- θ is angular displacement
Torsional Spring
In translational mechanical system, spring stores potential energy. Similarly, in rotational mechanical system, torsional spring stores potential energy.
If a torque is applied on torsional spring K, then it is opposed by an opposing torque due to the elasticity of torsional spring. This opposing torque is proportional to the angular displacement of the torsional spring. Assume that the moment of inertia and friction are negligible.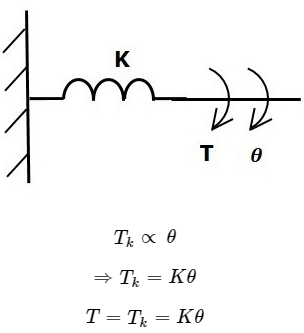
Where,
- T is the applied torque
- Tk is the opposing torque due to elasticity of torsional spring
- K is the torsional spring constant
- θ is angular displacement
Dashpot
If a torque is applied on dashpot B, then it is opposed by an opposing torque due to the rotational friction of the dashpot. This opposing torque is proportional to the angular velocity of the body. Assume the moment of inertia and elasticity are negligible.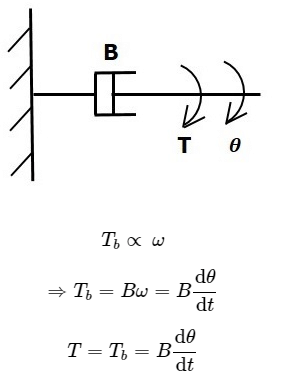
|
53 videos|115 docs|40 tests
|





















