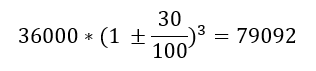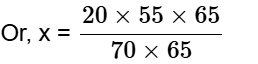Overview: Percentages | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| What is Percentage? |

|
| Concept of Percentage |

|
| Percentage Increase and Decrease |

|
| Application of Percentages |

|
| Important formulas |

|
| Solved Examples |

|
Introduction
- The chapter on Percentages forms one of the most important chapters (apart from Number Systems) in various competitive exams. The importance of ‘percentages’ is accentuated by the fact that there are many questions related to the use of percentages in all chapters of commercial arithmetic (especially Profit and Loss, Ratio and Proportion, Time and Work, and Time, Speed and Distance).
- Besides, the calculation skills you develop while reviewing the percentages chapter will help you handle Data Interpretation (DI) calculations. A closer look at that topic will yield that at least 80% of the total calculations in any DI paper constitute calculations on additions and percentages.
What is Percentage?
‘Percent’ as the name suggests ‘per’ means every and ‘cent’ means hundred i.e. “for every hundred”. It is an important tool for the comparison of data and information.
Example: Ana got 20 marks out of 40. Then, how many marks did she get when compared to 100?
Sol:
Solving by unitary method:
In the total of 40 marks, Ana got 20 marks Then,
In the total of 100 marks, Ana would have got = 20/40 x100 = 50 marks
It is just that when expressed in terms of hundred, it becomes percent.
That means to say Ana got 50%.
Concept of Percentage
- A percentage can only be calculated if it has a base value or denominator.
- In the above example, the base value or denominator was 40, which means that Ana secured 20 marks out of 40 (which is the base value of the calculation of marks secured.)
- Concept of percent change = (Final value – initial value)/ initial value x 100

Note: Initial value is taken as base or ‘denominator’ while calculating percent change.
Percentage Increase and Decrease
Percentages are often used to indicate changes in a quantity. A Percentage is a good measure to compare the change in two different quantities depending on the initial (or base) value of the quantity. For instance:

- If a quantity increases by a% then its value gets multiplied by (100 + a)/100
- If a quantity decreases by a% then its value gets multiplied by (100 - a)/100
Absolute Value Change vs Percentage Change
- Absolute value change = Actual change that happens in the measure of the quantity
- Percentage change = Absolute change with respect to the measure of the original quantity
- Two quantities may have different Percentage changes for the same value of Absolute value change, depending on the original value
Example: If the average humidity in a city increases from 32% in 2018 to 60% in 2019, what is the actual change and percentage change in humidity?
Sol:
Absolute value = Final value - Original value
= 60 - 32 = 28
Percentage change = (Final value - Original value)/ Original value
= 28/32 * 100 = 87.5%
Percent Point Change vs Percentage Change
- It is very important to understand the difference between the percent change and percent point change.
- Let us understand the difference between them by the following example:
Ana secured 70 percent marks in her last term exam.
Now, when we say that her marks increased by 5 percent, this means that there is an increase of 5% marks when compared to the last marks she secured, which is 5% of 70% = 3.5%
Her new secured marks will be 70 + 3.5 = 73.5%
Now, when we say that her marks increased by 5 percentage points, this means that there is an absolute increase of 5% in her marks, irrespective of the last marks she secured, which is her newly secured marks will be 70 + 5% = 75%
Therefore,
Percentage Point Change = Difference of two percentage figures
Application of Percentages
1. Population:
If the original population of a town is P and the annual increase is r%, then the population in n years is P' is
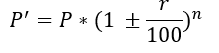
Example: The Population of Boisar is currently 36000 people. If the population increases by 30% each year, what will be the population 3 years from now?
Sol:
Population = 36000
r = 30% and n = 3 years
Hence the required population is:
2. Depreciation of Value:
The Value of any asset decreases with time due to any number of factors, including wear and tear, outdated technology, usage, etc. This is called depreciation.
If P is the original value and r is the rate of depreciation per year, then the final value (F) after n number of years is given as:
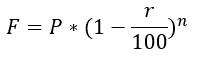
Example: An iPhone bought in 2022 has depreciated by 10% every year. If Mausam bought an iPhone for Rs. 72,600 in 2022. What is its value in 2025, on the same date?
Sol:
P = 72,600, r = 10%, n = 3 yearsF = 52,295.4
Important formulas
Finding Percentage of a Number:
- Formula: Percentage = (Value × Percentage) / 100
- Example: Find 25% of 200.
Percentage = (200 × 25) / 100 = 50
Finding the Value from a Percentage:
- Formula: Value = (Percentage × Total) / 100
- Example: What is 30% of 500?
Value = (30 × 500) / 100 = 150
Percentage Increase or Decrease:
- Formula: Percentage Change = [(New Value - Old Value) / Old Value] × 100
- Example: If the price of a book increases from 200 to 250, the percentage increase is:
Percentage Change = [(250 - 200) / 200] × 100 = 25%
Finding the Total Value from a Percentage:
- Formula: Total = (Value × 100) / Percentage
- Example: If 20% of a number is 50, find the total.
Total = (50 × 100) / 20 = 250
Convert a Fraction to Percentage:
- Formula: Percentage = (Fraction × 100)%
- Example: Convert 3/4 to a percentage.
Percentage = (3/4) × 100 = 75%
Finding the Percentage Profit or Loss:
- Formula: Profit or Loss Percentage = [(Profit or Loss) / Cost Price] × 100
- Example: If an item is bought for 100 and sold for 120,
Profit Percentage = [(120 - 100) / 100] × 100 = 20%
Solved Examples
Example 1: A report consists of 20 sheets each of 55 lines, and each such line consists of 65 characters. This report is reduced onto sheets each of 65 lines such that each line consists of 70 characters. The percentage reduction in the number of sheets is closest to:
Sol:
Let x be the page required when report is retyped
Now, we can use work equivalence method
20 × 55 × 65 = 70 × 65 × x
Or, x = 15.70 = 16 pages.
Example 2: 2/5th of the voters promise to vote for A, and the rest promise to vote for B. Of these, on the last day, 15% of the voters went back on their promise to vote for A, and 25% of voters went back on their promise to vote for B, and A lost by 200 votes. Then, the total number of voters is:
Sol:
Let the total numbers voters be 500
Voters promise to vote for A,
⇒ 2/5 × 500
⇒ 200
Remaining promised to vote for B,
⇒ 300 promised to vote for B
15% went back to vote for A,
⇒ 15/100 × 200
⇒ 30 voters who promised to vote for A voted for B,
25% went back to vote for B,
⇒ 25/100 × 300
⇒ 75 voters who promised to vote for B voted for A,
Final votes of B,
⇒ 300 – 75 + 30
⇒ 255
Final votes of A,
⇒ 200 – 30 + 75
⇒ 245
A lost by 255 – 245 = 10 votes,
According to the questions,
⇒ 10 = 200
⇒ 1 = 200/10 = 20
Total number of voters = 500 × 20 = 10,000∴ Total number of voters is 10,000
Example 3. A person who has a certain amount with him goes to market. He can buy 50 oranges or 40 mangoes. He retains 10% of the amount for taxi fares and buys 20 mangoes, and of the balance, he purchases oranges. The number of oranges he can purchase is:
Sol:
The person can buy 50 oranges or 40 mangoes.
Let the price of one orange be Rs. x
The total amount the person has = Rs. 50x
40 mangoes cost 50x, So one mango costs 1.25x
10% of the total amount is retained for taxi fare = 10% of 50x = 5x
20 mangoes bought for 20 * 1.25x = 25x
Money left with the person = 50x – (Taxi fare) – (Mangoes cost) = 50x – 5x – 25x = 20x
One Orange was for Rs. x, Therefore, 20 oranges can be bought with Rs. 20 x
Thus, the person bought 20 oranges.
Example 4. Forty percent of the employees of a certain company are men, and 75% of the men earn more than Rs. 25,000 per year. If 45% of the company’s employees earn more than Rs. 25,000 per year, what fraction of the women employed by the company earned Rs. 25,000 or less per year?
Sol:
Let the total number of employees in the company be x
Then the number of men and women be 0.4x and 0.6x, respectively.
75% of men earn more than Rs. 25000 ⇒ 0.75 x 0.4 x = 0.3 x
Total number of employees earning more than Rs. 25000 = 45% x = 0.45 x
Number of women earning more than Rs. 25000 = Total employees earning more than Rs. 25000 – total number of Men earning more than Rs. 25000 = 0.45 x – 0.30 x = 0.15 x
Number of the women earning Rs. 25000 or less = 0.60 x – 0.15 x = 0.45 x
Fraction of the women employed by the company who earn Rs. 25000 or less = (0.45x/0.60x) = 45/60 = 3/4
Example 5: In a class of 60 students, 20% are male. 75% of female students passed an exam conducted for the whole class. What is the number of female students who passed the exam?
Sol: Since it is given that 20% of students are male, that means the remaining 80% are females.
Number of females - (80/100)x60 = 48
Number of female students who passed = 75% of 48 = 36
|
208 videos|272 docs|138 tests
|
FAQs on Overview: Percentages - CSAT Preparation - UPSC
| 1. What is the definition of a percentage? |  |
| 2. How do you calculate percentage increase? |  |
| 3. What is the difference between percentage increase and percentage decrease? |  |
| 4. In what real-life situations are percentages commonly used? |  |
| 5. Can you give an example of how to apply percentages in financial calculations? |  |