Irodov Solutions: Conductors And Dielectrics In An Electric Field- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 54. A small ball is suspended over an infinite horizontal conducting plane by means of an insulating elastic thread of stiffness k. As soon as the ball was charged, it descended by x cm and its separation Horn the plane became equal to l. Find the charge of the ball.
Solution. 54. When the ball is charged, for the equilibrium of ball, electric force on it must counter balance the excess spring force, exerted, on the ball due to the extension in the soring.
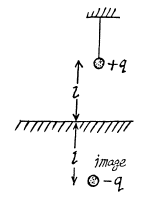
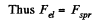
or,  (The force on the charge q might be considered as arised from attraction by the electrical image)
(The force on the charge q might be considered as arised from attraction by the electrical image)
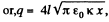
sought charge on the sphere.
Q. 55. A point charge q is located at a distance l from the infinite conducting plane. What amount of work has to be performed in order to slowly remove this charge very far from the plane.
Solution. 55. By definition, the work of this force done upon an elementry displacement dx (Fig.) is given by
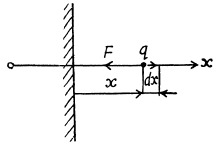

where the expression for the force is obtained with the help of the image method. Integrating this equation over x between l and ∞, we find
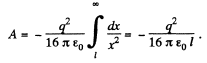
Q. 56. Two point charges, q and —q, are separated by a distance 1, both being located at a distance l/2 from the infinite conducting plane. Find:
(a) the modulus of the vector of the electric force acting on each charge;
(b) the magnitude of the electric field strength vector at the midpoint between these charges.
Solution. 56. (a) Using the concept of electrical image, iit is clear that the magnitude of the force acting on each charge,
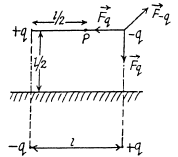
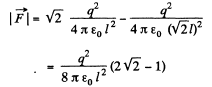
(b) Also, from the figure, magnitude of electrical field strength at P
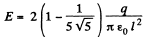
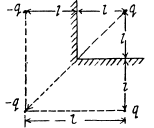
Q. 57. A point charge q is located between two mutually perpendicular conducting half-planes. Its distance from each half-plane is equal to l. Find the modulus of the vector of the force acting on the charge.
Solution. 57. 7 Using the concept of electrical image, it is easily seen that the force on the charge q is,
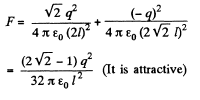
Q. 58. A point dipole with an electric moment p is located at a distance l from an infinite conducting plane. Find the modulus of the vector of the force acting on the dipole if the vector p is perpendicular to the plane.
Solution. 58. Using the concept of electrical image, force on the dipole 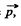

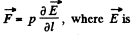 field at the location of
field at the location of
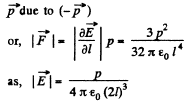
Q. 59. A point charge q is located at a distance l from an infinite conducting plane. Determine the surface density of charges induced on the plane as a function of separation r from the base of the perpendicular drawn to the plane from the charge.
Solution. 59. To find the surface charge density, we must know the electric field at the point P (Fig.) which is at a distance r from the point O.
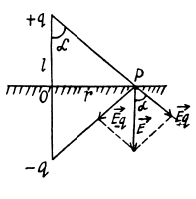
Using the image mirror method, the field at P,

Now from Gauss’ theorem the surface charge density on conductor is connected with the electric field near its surface (in vaccum) through the relation 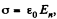 where En is the projection of
where En is the projection of  the outward normal
the outward normal 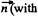 respect to the conductor).
respect to the conductor).
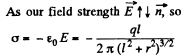
Q. 60. A thin infinitely long thread carrying a charge λ per unit length is oriented parallel to the infinite conducting plane. The distance between the thread and the plane is equal to l. Find:
(a) the modulus of the vector of the force acting on a unit length of the thread;
(b) the distribution of surface charge density σ (x) over the plane, where x is the distance from the plane perpendicular to the conducting surface and passing through the thread.
Solution. 60. (a) The force F1 on unit length of the thread is given by
F1 = λ E1
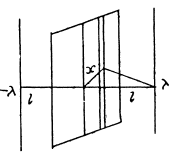
where E1 is the field at the thread due to image charge :
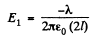
Thus 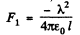
minus singn means that the force is one of attraction.
(b) There is an image thread with charge density- λ behind the conducting plane. We calculate the electric field on the conductor. It is
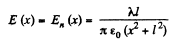
on considering the thread and its image.
Thus
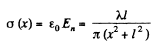
Q. 61. A very long straight thread is oriented at right angles to an infinite conducting plane; its end is separated from the plane by a distance l. The thread carries a uniform charge of linear density λ. Suppose the point 0 is the trace of the thread on the plane. Find the surface density of the induced charge on the plane
(a) at the point 0;
(b) as a function of a distance r from the point 0.
Solution. 61.
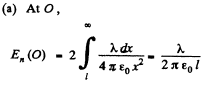
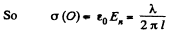
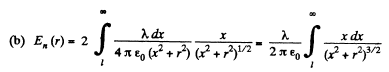
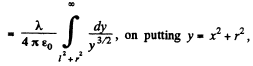
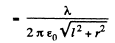
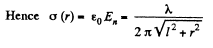
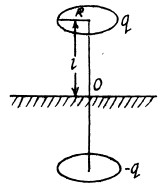
Q. 62. A thin wire ring of radius R carries a charge q. The ring is oriented parallel to an infinite conducting plane and is separated by a distance l from it. Find:
(a) the surface charge density at the point of the plane symmetrical with respect to the ring;
(b) the strength and the potential of the electric field at the centre of the ring.
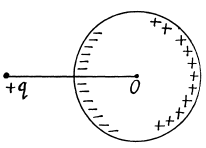
Solution. 62. It can be easily seen that in accordance with the image method, a charge -q must be located on a similar ring but on the other side of the conducting plane. (Fig.) at the same nernendicular distance. From the solution of 3.9 net electric field at O,
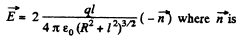
outward normal with respect to the conducting plane.
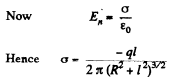
where minus sign indicates that the induced carge is opposite in sign to that of chaige q > 0.
Q. 63. Find the potential φ of an uncharged conducting sphere outside of which a point charge q is located at a distance l from the sphere's centre.
Solution. 63. Potential φ is the same for all the points of the sphere. Thus we calculate its value at the centre O of the sphere. Thus we can calculate its value at the centre O of the sphere, because only for this point, it can be calculated in the most simple way.
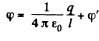 (1)
(1)
where the first term is the potential of the charge q, while the second is the potential due to the charges induced on the surface of the sphere. But since all induced charges are at the same distance equal to the radius of the circle from the point C and the total induced charge is equal to zero, φ' = 0, as well. Thus equation (1) is reduced to the form, 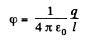
Q. 64. A point charge q is located at a distance r from the centre O of an uncharged conducting spherical layer whose inside and outside radii are equal to R1 and R2 respectively. Find the potential at the point O if r < R1.
Solution. 64. As the sphere has conducting layers, charge -q is induced on the inner surface of the sphere q and consequently chaige + q is induced on the outer layer as the sphere as a whole is uncharged.
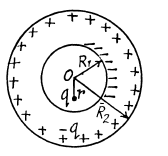
Hence, the potential at O is given by,
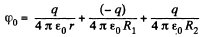
It should be noticed that the potential can be found in such a sim ple way only at O, since all the induced charges are at the same distance from this point, and their distribution, (which is unknown to us), does not play any role.
Q. 65. A system consists of two concentric conducting spheres, with the inside sphere of radius a carrying a positive charge q1. What charge q2 has to be deposited on the outside sphere of radius b to reduce the potential of the inside sphere to zero? How does the potential φ depend in this case on a distance r from the centre of the system? Draw the approximate plot of this dependence.
Solution. 65. Potential at the inside sphere,
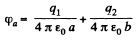
O bviously 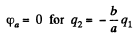 (1)
(1)
When 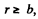

And when 
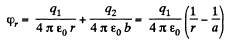
Q. 66. Four large metal plates are located at a small distance d from one another as shown in Fig. 3.8. The extreme plates are inter-connected by means of a conductor while a potential difference Δφ is applied to internal plates. Find:
(a) the values of the electric field strength between neighbouring plates;
(b) the total charge per unit area of each plate.
Solution. 66. (a) As the metallic plates 1 and 4 are isolated and conncted by means of a conductor, φ1 = φ4. Plates 2 and 3 have the same amount of positive and negative charges and due to induction, plates 1 and 4 are respectively negatively and positively charged and in addition to it all the four plates are located a small but at equal distance d relative to each other, the magnitude o f electric field strength between 1 - 2 and 3 - 4 are both equal in magnitude and direction 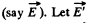 be the field strength between the plates 2 and 3 which is directed form 2 to 3. Hence
be the field strength between the plates 2 and 3 which is directed form 2 to 3. Hence 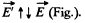
According to the problem
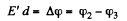 (1)
(1)
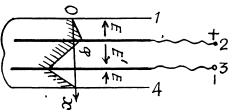
In addition to
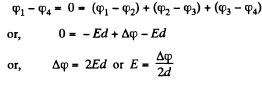
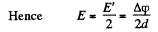 (2)
(2)
(b) Since E α σ, we can state that according to equation (2) for part (a) the charge on the p4te 2 is divided into two parts; such that 1/3 rd of it lies on the upper side and 2/3 rd on its lower face.
Thus charge density of upper face of plate 2 or of plate 1 or plate 4 and lower face of
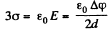 and charge density of lower face of 2 or upper face of 3
and charge density of lower face of 2 or upper face of 3

Hence the net charge density of plate 2 or 3 becomes 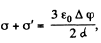 which is obvious from the argument.
which is obvious from the argument.
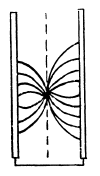
Q. 67. Two infinite conducting plates 1 and 2 are separated by a distance l. A point charge q is located between the plates at a distance x from plate 1. Find the charges induced on each plate.
Solution. 67. The problem of point charge between two conducting planes is more easily tackled (if we want only the total charge induced on the planes) if we replace the point charge by a uniformly charged plane sheet.
Let σ be the charge density on this sheet and E1, E2 outward electric field on the two sides of this sheet.
Then 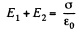
The conducting planes will be assumed to be grounded. 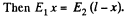
Hence 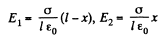
This means that the induced charge density on the plane conductors are

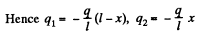
Q. 68. Find the electric force experienced by a charge reduced to a unit area of an arbitrary conductor if the surface density of the charge equals σ.
Solution. 68. Near the conductor 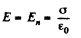
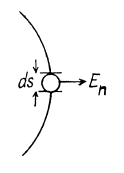
This field can be written as the sum of two parts E1 and E2 E1 is the electric field due to an infinitesimal area dS.
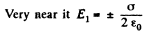
The remaining part contributes 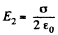 both sides. In calculating the force on the element dS we drop E1 (because it is a self-force.) Thus
both sides. In calculating the force on the element dS we drop E1 (because it is a self-force.) Thus
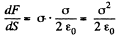
Q. 69. A metal ball of radius R = 1.5 cm has a charge q = 10 μC. Find the modulus of the vector of the resultant force acting on a charge located on one half of the ball.
Solution. 69. The total force on the hemisphere is
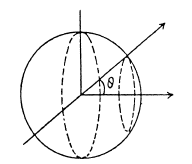
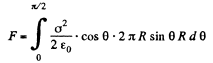
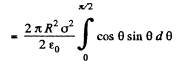
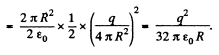
Q. 70. When an uncharged conducting ball of radius R is placed in an external uniform electric field, a surface charge density σ = σ0 cos θ is induced on the ball's surface (here ao is a constant, is a polar angle). Find the magnitude of the resultant electric force acting on an induced charge of the same sign.
Solution. 70. We know that the force acting on the area element dS of a conductor is,
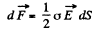 (1)
(1)
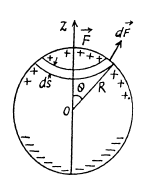
It follows from symmetry considerations that  directed along the z-axis, and hence it can be represented as the sum (integral) of the projection of elementary forces (1) onto the z-axis :
directed along the z-axis, and hence it can be represented as the sum (integral) of the projection of elementary forces (1) onto the z-axis :
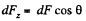 (2)
(2)
For simplicity let us consider an element area 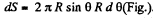 Now considering that
Now considering that  Equation (2) takes the from
Equation (2) takes the from
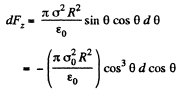
Integrating this expression over the half sphere (i.e. with respect to cos 0 between 1 and 0), we obtain
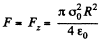
FAQs on Irodov Solutions: Conductors And Dielectrics In An Electric Field- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the difference between a conductor and a dielectric in an electric field? |  |
| 2. How does an electric field affect conductors and dielectrics differently? |  |
| 3. What is the concept of electric shielding by conductors? |  |
| 4. How does the presence of dielectrics affect the electric field in a capacitor? |  |
| 5. What are the factors that determine the choice between using a conductor or a dielectric in an electrical application? |  |

|
Explore Courses for JEE exam
|

|

















