Irodov Solutions: Conductors And Dielectrics In An Electric Field- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 86. Half the space between two concentric electrodes of a spherical capacitor is filled, as shown in Fig. 3.14, with uniform isotropic dielectric with permittivity ε. The charge of the capacitor is q. Find the magnitude of the electric field strength between the electrodes as a function of distance r from the curvature centre of the electrodes.
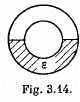
Solution. 86. At the interface of the dielectric and vacuum,
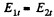
The electric field must be radial and
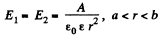
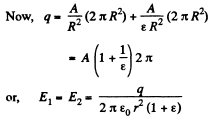
Q. 87. Two small identical balls carrying the charges of the same sign are suspended from the same point by insulating threads of equal length. When the surrounding space was filled with kerosene the divergence angle between the threads remained constant. What is the density of the material of which the balls are made?
Solution. 87. In air the forces are as shown. In K-oil,
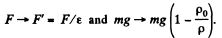
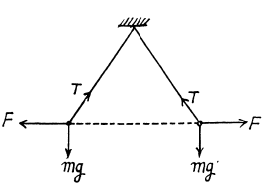
Since the inclinations do not change
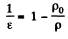
or, 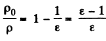
or, 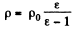
where p0 is the density of K-oil and p that of the material of which the balls are made.
Q. 88. A uniform electric field of strength E = 100 V/m is generated inside a ball made of uniform isotropic dielectric with permittivity ε = 5.00. The radius of the ball is R = 3.0 cm. Find the maximum surface density of the bound charges and the total bound charge of one sign.
Solution. 88. Within the ball the electric field can be resolved into normal and tangential components.
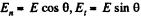
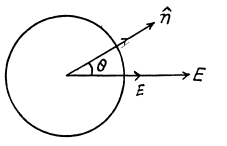
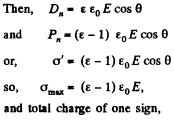
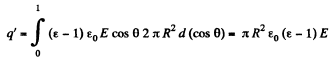
(Since we are interested in the total charge of one sign we must intergrate cos θ from 0 to 1 only).
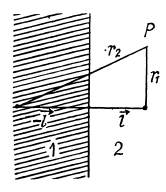
Q. 89. A point charge q is located in vacuum at a distance l from the plane surface of a uniform isotropic dielectric filling up all the half-space. The permittivity of the dielectric equals a. Find:
(a) the surface density of the bound charges as a function of distance r from the point charge q; analyse the obtained result at 1→0;
(b) the total bound charge on the surface of the dielectric.
Solution. 89. The chaige is at A in the medium 1 and has an image point at A’ in the medium 2. The electric field in the medium 1 is due to the actual charge q at A and the image charge q' at A'. The electric field in 2 is due to a corrected charge c[ at A. Thus on the boundary between 1 and 2,
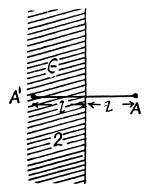
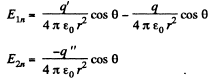
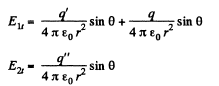
The boundary conditions are
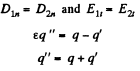
So, 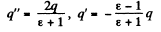
(a) The surface density of the bound charge on the surface of the dielectric
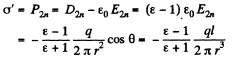
(b) Total bound charge 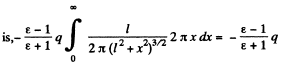
Q. 90. Making use of the formulation and the solution of the foregoing problem, find the magnitude of the force exerted by the charges bound on the surface of the dielectric on the point charge q.
Solution. 90. The force on the point chaige q is due to the bound charges. This can be calculated from the field at this chaige after extracting out the self field. This image field is
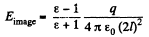
Thus, 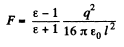
Q. 91. A point charge q is located on the plane dividing vacuum and infinite uniform isotropic dielectric with permittivity ε. Find the moduli of the vectors D and E as well as the potential q as functions of distance r from the charge q.
Solution. 91.
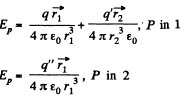
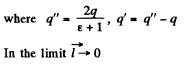
Thus,
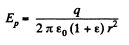
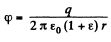
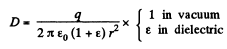
Q. 92. A small conducting ball carrying a charge q is located in a uniform isotropic dielectric with permittivity ε at a distance l from an infinite boundary plane between the dielectric and vacuum. Find the surface density of the bound charges on the boundary plane as a function of distance r from the ball. Analyse the obtained result for l→ 0.
Solution. 92.
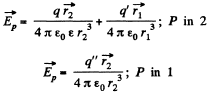
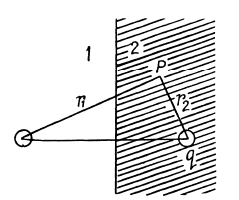
Using the boundary conditions,
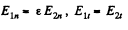
This implies
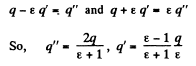
Then, as earlier,

Q. 93. A half-space filled with uniform isotropic dielectric with permittivity a has the conducting boundary plane. Inside the dielectric, at a distance l from this plane, there is a small metal ball possessing a charge q. Find the surface density of the bound charges at the boundary plane as a function of distance r from the ball.
Solution. 93. To calculate the electric field, first we note that an image charge will be needed to ensure that the electric field on the metal boundary is normal to the surface.
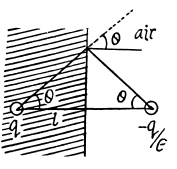
The image chaige must have magnitude 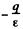
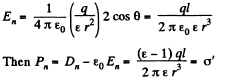
This is the density of bound charge on the surface.
Q. 94. A plate of thickness h made of uniform statically polarized dielectric is placed inside a capacitor whose parallel plates are interconnected by a conductor. The polarization of the dielectric is equal to P (Fig. 3.15). The separation between the capacitor plates is d. Find the strength and induction vectors for the electric field both inside and outside the plates.
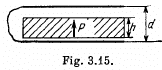
Solution. 94. Since the condenser plates are connected,
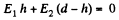
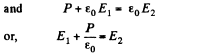
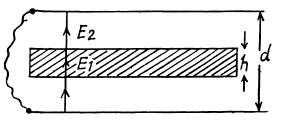
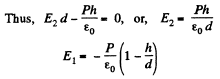
Q. 95. A long round dielectric cylinder is polarized so that the vector P = αr, where α is a positive constant and r is the distance from the axis. Find the space density p' of bound charges as a function of distance r from the axis.
Solution. 95. Given 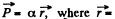 distance from the axis. The space density of charges is given by, p' = - div
distance from the axis. The space density of charges is given by, p' = - div 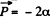
On using.
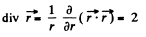
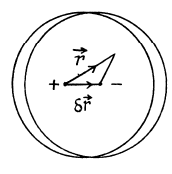
Q. 96. A dielectric ball is polarized uniformly and statically. Its polarization equals P. Taking into account that a ball polarized in this way may be represented as a result of a small shift of all positive charges of the dielectric relative to all negative charges,
(a) find the electric field strength E inside the ball;
(b) demonstrate that the field outside the ball is that of a dipole located at the centre of the ball, the potential of that field being equal to φ = p0r/4π ε0, where P0 is the electric moment of the ball, and r is the distance from its centre.
Solution. 96. In a uniformly charged sphere,
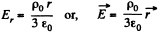
The total electric field is
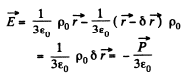
where 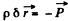 (dipole moment is defined with its direction being from the -vc chaige to +ve charge.)
(dipole moment is defined with its direction being from the -vc chaige to +ve charge.)
The potential outside is
 is the total dipole moment.
is the total dipole moment.
Q. 97. Utilizing the solution of the foregoing problem, find the electric field strength E0 in a spherical cavity in an infinite statically polarized uniform dielectric if the dielectric's polarization is P, and far from the cavity the field strength is E.
Solution. 97. The electric field  in a spherical cavity hi a uniform dielectric of permittivity e is related to the far away field
in a spherical cavity hi a uniform dielectric of permittivity e is related to the far away field 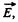 in the following mannenjmagine the cavity to be filled wp with the dielectric. Then there will be a uniform
in the following mannenjmagine the cavity to be filled wp with the dielectric. Then there will be a uniform  everywhere and a polarization
everywhere and a polarization 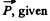 by,
by,
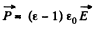
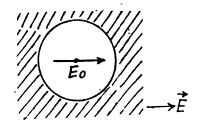
Now take out the sphere making the cavity, the_£lectric field inside the sphere will be
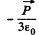
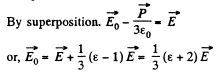
Q. 98. A uniform dielectric ball is placed in a uniform electric field of strength E0. Under these conditions the dielectric becomes polarized uniformly. Find the electric field strength E inside the ball and the polarization P of the dielectric whose permittivity equals e. Make use of the result obtained in Problem Q.96.
Solution. 98. By superposition the field  the bll is given by
the bll is given by
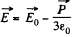
On the other hand, if the sphere is not too small, the macroscopic equation 
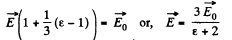
Also 
Q. 99. An infinitely long round dielectric cylinder is polarized uniformly and statically, the polarization P being perpendicular to the axis of the cylinder. Find the electric field strength E inside the dielectric.
Solution. 99. This is to be handled by the same trick as in Q.96. We have effectively a two dimensional situation. For a uniform cylinder full of charge with chaige density p0 (charge per unit volume), the electric field E at an inside point is along the (cylindrical) radius vector  and equal to,
and equal to,
Therefore the polarized cylinder can be thought of as two equal and opposite charge distributions displaced with respect to each other
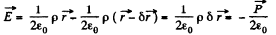
Since 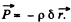 (direction of electric dipole moment vector being from the negative charge to positive charge .)
(direction of electric dipole moment vector being from the negative charge to positive charge .)
Q. 100. A long round cylinder made of uniform dielectric is placed in a uniform electric field of strength E0. The axis of the cylinder is perpendicular to vector E0. Under these conditions the dielectric becomes polarized uniformly. Making use of the result obtained in the foregoing problem, find the electric field strength E in the cylinder and the polarization P of the dielectric whose permittivity is equal to ε.
Solution. 100. As in Q.98, we write 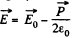
using here the result of the foregoing problem.
Also 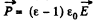
So, 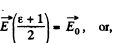

FAQs on Irodov Solutions: Conductors And Dielectrics In An Electric Field- 3 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the difference between conductors and dielectrics in an electric field? |  |
| 2. How does an electric field affect conductors and dielectrics differently? |  |
| 3. Can a conductor become an insulator in an electric field? |  |
| 4. What happens when a dielectric is placed in an electric field? |  |
| 5. How does the presence of dielectrics affect the capacitance of a capacitor in an electric field? |  |

|
Explore Courses for JEE exam
|

|

















